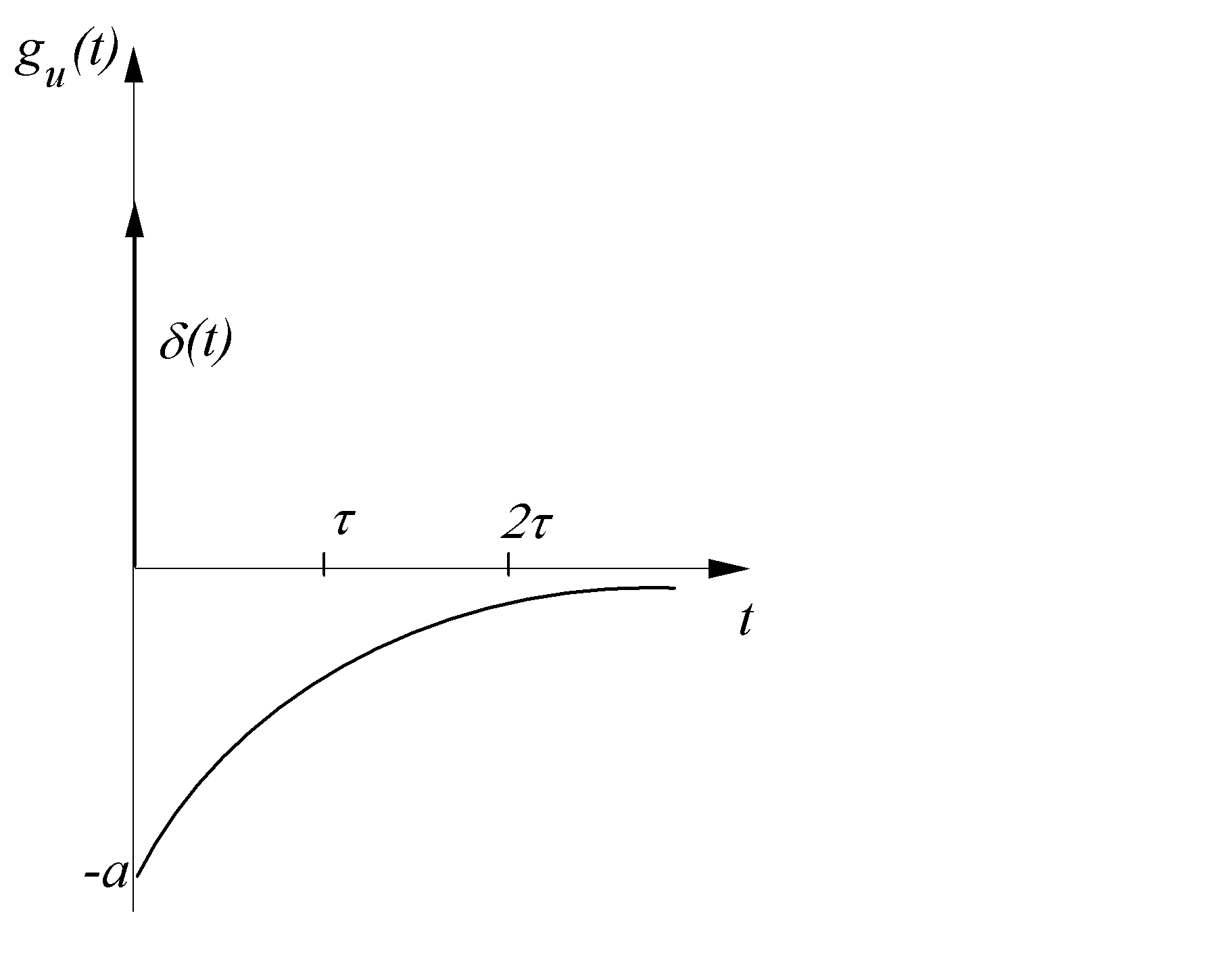3.2. Импульсная характеристика цепи

Импульсная (весовая) характеристика или импульсная функция цепи – это ее обобщенная характеристика, являющаяся временной функцией, численно равная реакции цепи на единичное импульсное воздействие на ее входе при нулевых начальных условиях (рис. 13.14); другими словами, это отклик цепи, свободной от начального запаса энергии на дельта-функцию Дирана на ее входе.

Рис. 13.14

Функцию можно определить, рассчитав переходную или передаточную функцию цепи.

Расчет функции с использованием переходной функции цепи. Пусть при входном воздействии реакцией линейной электрической цепи является . Тогда в силу линейности цепи при входном воздействии, равном производной , реакция цепи будет равна производной .

Как отмечалось, при , реакция цепи , а если , то реакция цепи будет , т.е. импульсная функция

.

Согласно свойству выборки произведение . Таким образом, импульсная функция цепи

. (13.8)

Если , то импульсная функция имеет вид

. (13.9)

Следовательно, размерность импульсной характеристики равна размерности переходной характеристики, поделенной на время.

Расчет функции с использованием передаточной функции цепи. Согласно выражению (13.6), при воздействии на вход функции , откликом функции будет переходная функция вида:

.

С другой стороны, известно, что изображение производной функции по времени , при , равно произведению .

Откуда ,

или , (13.10)

т.е. импульсная характеристика цепи равна обратному преобразованию Лапласа ее передаточной функции.

Пример. Найдем импульсную функцию цепи, схемы замещения которой представлены на рис. 13.12, а; 13.13.

Решение

Переходная и передаточная функции этой цепи били получены ранее:

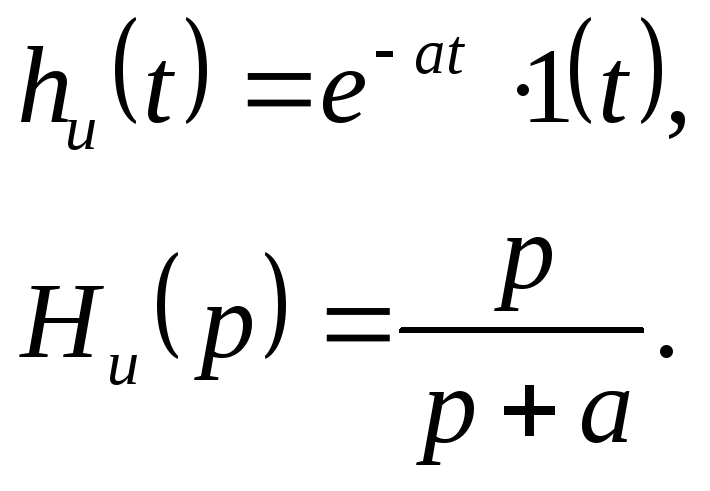
Тогда, согласно выражению (13.8)

,

где .

Рис. 13.15.

График импульсной характеристики цепи представлен на рис. 13.15.

Выводы

Импульсная характеристика введена по тем же двум причинам, что и переходная характеристика .

1. Единичное импульсное воздействие – скачкообразное и потому довольно тяжелое для любой системы или цепи внешнее воздействие. Следовательно, важно знать реакцию системы или цепи именно при таком воздействии, т.е. импульсную характеристику .

2. При помощи некоторого видоизменения интеграла Дюамеля можно, зная вычислить реакцию системы или цепи на любое внешнее возмущение (см. далее пп. 13.4, 13.5).

4. Интеграл наложения (дюамеля).

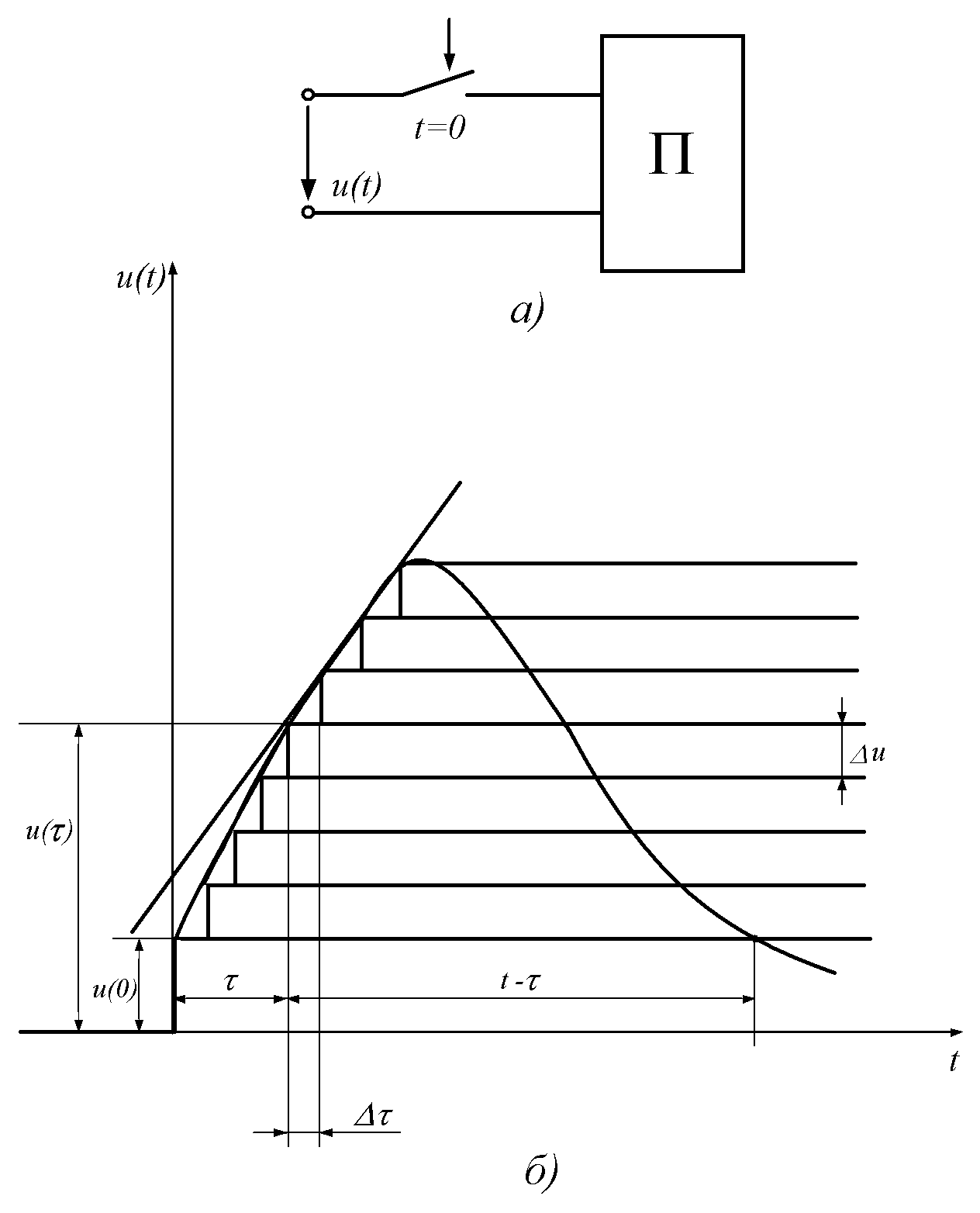
Пусть произвольный пассивный двухполюсник (рис. 13.16, а) подключается к источнику непрерывно изменяющегося с момента напряжения(рис. 13.16,б).

Рис. 13.16.

Требуется найти ток (или напряжение) в любой ветви двухполюсника после замыкания ключа.

Задачу решим в два этапа. Сначала искомую величину найдем при включении двухполюсника на единичный скачок напряжения, который задается единичной ступенчатой функцией .

Известно, что реакцией цепи на единичный скачок является переходная характеристика (функция) .

Например, для – цепи переходная функция по току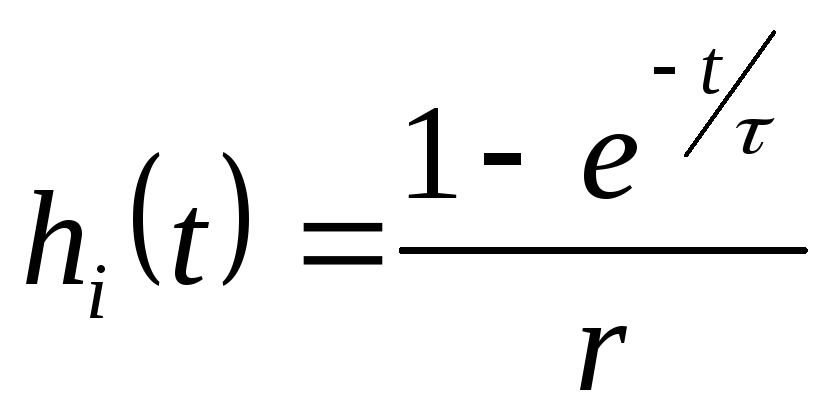(см. п.2.1), для– цепи переходная функция по напряжению.

На втором этапе непрерывно изменяющееся напряжение заменим ступенчатой функцией с элементарными прямоугольными скачками(см. рис. 13.16б). Тогда процесс изменения напряжения можно представить как включение при постоянного напряжения, а затем как включение элементарных постоянных напряжений, смещенных относительно друг друга на интервалы времении имеющих знак плюс для возрастающей и минус для падающей ветви заданной кривой напряжения.

Составляющая искомого тока в момент от постоянного напряженияравна:

.

Составляющая искомого тока от элементарного скачка напряжения , включаемого в момент времениравна:

.

Здесь аргументом переходной функции является время , поскольку элементарный скачок напряженияначинает действовать на времяпозднее замыкания ключа или, иначе говоря, поскольку промежуток времени между моментомначала действия этого скачка и моментом времениравен.

Элементарный скачок напряжения

,

где – масштабный коэффициент.

Поэтому искомая составляющая тока

.

Элементарные скачки напряжения включаются на интервале времени от до момента, для которого определяется искомый ток. Поэтому, суммируя составляющие тока от всех скачков, переходя к пределу при, и учитывая составляющую тока от начального скачка напряжения, получаем:

.

Последняя формула для определения тока при непрерывном изменении приложенного напряжения

(13.11)

называется интегралом наложения (суперпозиции) или интегралом Дюамеля (первой формой записи этого интеграла).

Аналогично решается задача при подключении цепи и источнику тока. Согласно этому интегралу реакция цепи, в общем виде, в некоторый моментпосле начала воздействияопределяется всей той частью воздействия, которая имела место до момента времени.

Заменой переменных и интегрированием по частям можно получить другие формы записи интеграла Дюамеля, эквивалентные выражению (13.11):

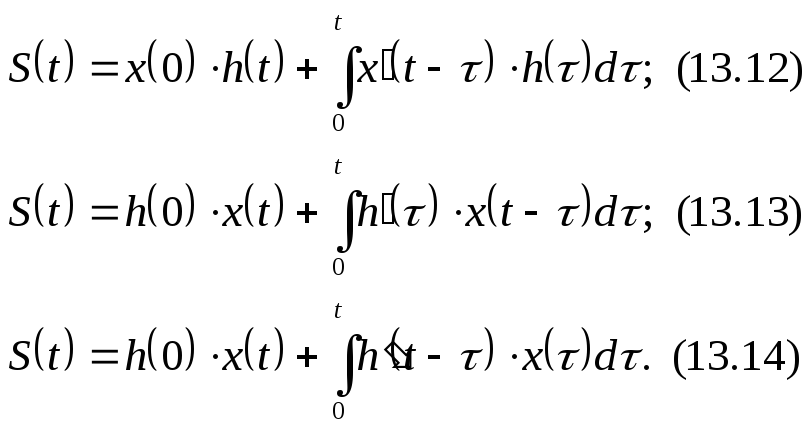
Выбор формы записи интеграла Дюамеля определяется удобством расчета. Например, в случае, если выражается экспоненциальной функцией, удобной оказывается формула (13.13) или (13.14), что обуславливается простотой дифференцирования экспоненциальной функции.

При илиудобно применять форму записи, в которой слагаемое перед интегралом обращается в нуль.

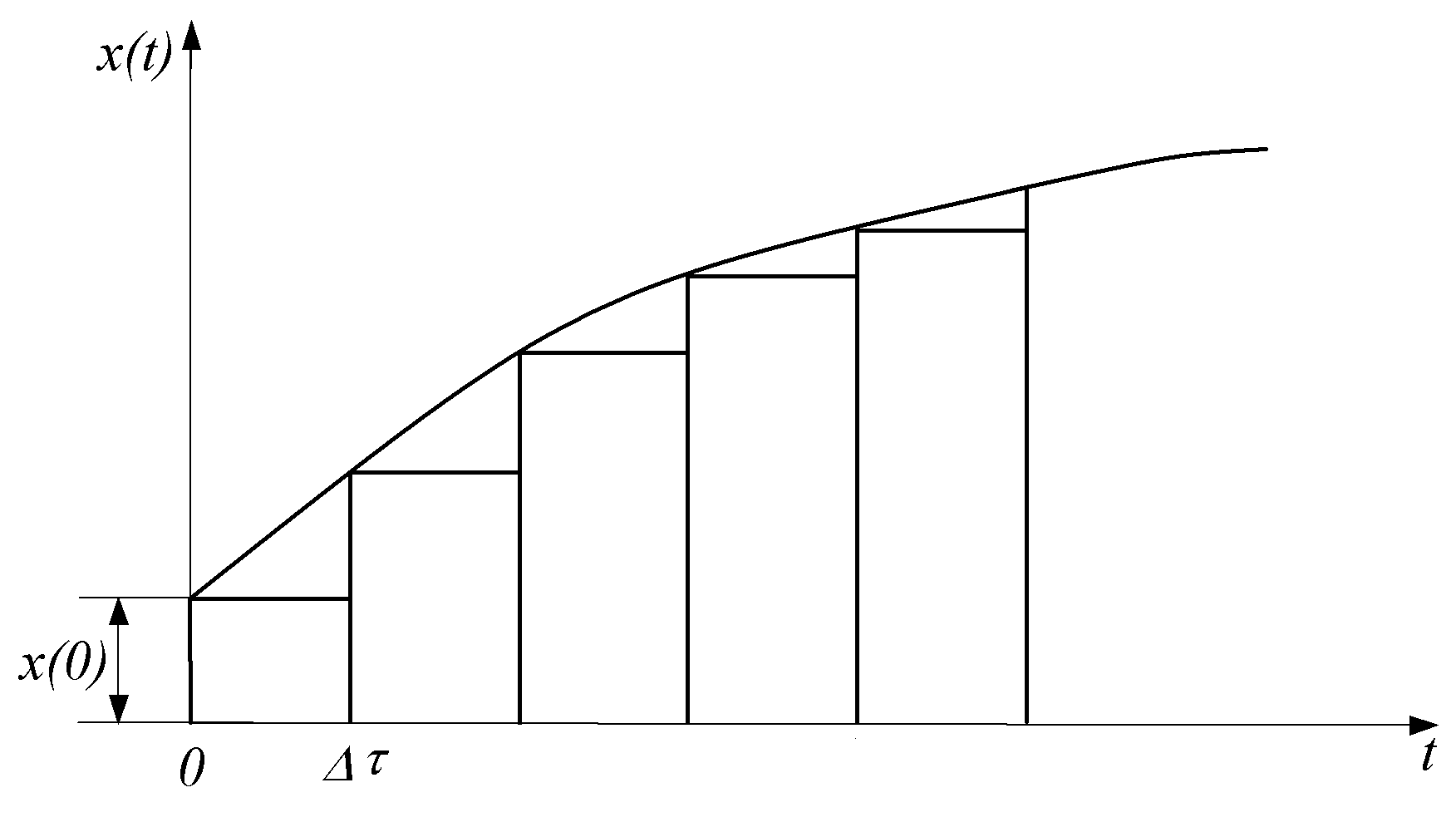
Произвольное воздействие может быть представлено также в виде суммы последовательно включаемых импульсов, как это изображено на рис. 13.17.

Рис. 13.17.

При бесконечно малой длительности импульсов получим формулы интеграла Дюамеля, аналогичные (13.13) и (13.14).

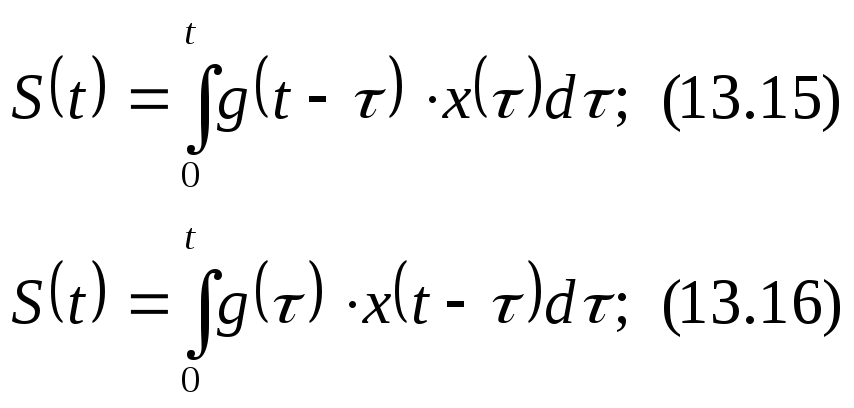
Эти же формулы можно получить из соотношений (13.13) и (13.14), заменив а них производную функцию импульсной функцией.

Вывод.

Таким образом, на основе формул интеграла Дюамеля (13.11) – (13.16) и временных характеристик цепи имогут быть определены временные функции откликов цепина произвольные воздействия.