4. Описание стационарных временных рядов с помощью авторегрессионной модели

В п. 1.4 был рассмотрен класс стационарных процессов, в рамках которого подбирается модель, пригодная для описания случайных остатков E_t анализируемого временного ряда. В этом параграфе мы рассмотрим модели авторегрессии, с помощью которых можно описать поведение стационарных случайных остатков. Предположим, что исследуемый временной ряд представляет собой стационарный случайный процесс, т. е. Y_t = E_t.

Модель стационарного процесса, выражающая, значение показателя y_t в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей, называется авторегрессионной моделью (АРМ).

В общем виде авторегрессионный процесс может быть представлен как

(4.1)

где a_j — параметры модели (4.1), которые оцениваются методом наименьших квадратов или с помощью коэффициентов автокорреляции (коэффициенты а_j для стационарных процессов по абсолютной величине меньше единицы);

р — порядок процесса авторегрессии, определяющий количество периодов, от которых зависит текущее значение y_t;

ε_t — случайная составляющая, имеющая нормальное распределение с нулевым математическим ожиданием и дисперсией .

4.1. Оценка параметров авторегрессионной модели

Рассмотрим оценку параметров авторегрессионной модели методом наименьших квадратов и методом коэффициентов автокорреляции.

Как известно, метод наименьших квадратов основывается на требовании минимизации дисперсии, и это условие для АРМ выглядит следующим образом:

.

Это требование приводит к системе нормальных уравнений

Решая систему относительно а_j, получим коэффициенты авторегрессии (4.1).

При оценке параметров авторегрессионной модели (4.1) также можно использовать метод, который основывается на вычислении коэффициентов автокорреляции. Для вычисления параметров модели (4.1) решается система Юла — Уокера

(4.2)

где r_k (k = 1, 2, 3, …, p) — коэффициенты автокорреляции, которые рассчитываются по формуле (1.10).

На практике чаще всего встречаются два случая АРМ: авторегрессия 1-го и 2-го порядков.

П р и м е р 4.1. Процесс авторегрессии 1-го порядка описывается моделью

Единственный коэффициент модели равен коэффициенту автокорреляции 1-го порядка: a₁= r₁. Если а₁ > 0, то автокорреляционная функция является затухающей экспонентой, при а₁ < 0 - затухающей синусоидой (рис. 4.1 а, б).

П р и м е р 4.2. Процесс авторегрессии 2-го порядка описывается моделью

Подставляя р = 2 в систему, уравнений (4.2), получим:

Решая эту систему относительно а₁ и a₂, приходим к следующим отношениям

;

Условие стационарности накладывает следующие ограничения на изменение коэффициентов а₁ и а₂:

a₁ + a₂ < 1; a₂ - a₁ < 1; -1 < a₂ < 1

Коррелограмм для авторегрессионной модели 2-го порядка представлен на рис. 4.1, в.

Рис. 4.1. Автокорреляционная функция для модели авторегрессии:

а — 1-го порядка, когда а₁ > 0;

б — 1-го порядка, когда а₁ < 0;

в — 2-го порядка

4.2. Определение порядка авторегрессии

Определение порядка авторегрессии является одним из важнейших этапов при построении авторегрессионных моделей. Предварительная оценка на основе экономического анализа позволяет выделить те значения исследуемого показателя, которые оказали значительное влияние на его изменения в последующие периоды. Низкий порядок авторегрессии может дать несущественные результаты за счет того, что в модели не использована информация о предыдущем. Повышение порядка в отдельных случаях также может привести к снижению качества модели. Поэтому определение порядка является важным этапом построения АРМ.

Для определения порядка авторегрессии следует использовать такие характеристики, как автокорреляционная функция и частная автокорреляционная функция.

Понятие автокорреляционной функции было дано в п. 1.4. Для стационарных процессов автокорреляционная функция затухает с ростом τ. По скорости затухания могут быть сделаны выводы о порядке модели. Эти выводы сравниваются с результатами анализа частной автокорреляционной функции.

Для определения частной автокорреляционной функции рассматривается матрица

состоящая из коэффициентов автокорреляции ряда. Частная автокорреляционная функция определяется как отношение

,

где R^{1 k+1} — алгебраическое дополнение элемента 1-й строки и (k + 1)-го столбца;

R^{1 1} — алгебраическое дополнение 1-й строки и 1-го столбца матрицы R_k+1.

Для k = 1, 2, 3 значения автокорреляционной функции соответственно равны:

R(1) = r₁; ;.

Коэффициент при последнем члене авторегрессии порядка р (4.1) совпадает с р-м значением частной автокорреляционной функции R(p), т. е. R(p) = а_р(р), р = 1, 2, ... . И если исследуемый процесс является авторегрессией порядка р, то а_р(р) ≠ 0, а a_q(q) = 0 для всех q > р. На основании этого признака можно судить о порядке авторегрессии.

Так как мы имеем дело не с теоретическими, а с оценочными значениями автокорреляционной функции, то для подтверждения порядка авторегрессионной модели можно воспользоваться статистическим критерием Бартлетта, суть которого заключается в проверке гипотезы о том, что авторегрессионная модель порядка q (р <q < ) дает лучшую аппроксимацию, чем модель порядка р. Для этого строят модель порядка q и определяют суммы квадратов отклонений для тех наблюдений, для которых y_t можно вычислить как с помощью моделей порядка р, так и с помощью моделей порядка q.

Пусть — сумма квадратов остатков для модели порядка р (штрих означает, что рассматриваются не все остатки, а лишь те, для которых определена и модель порядка q);— сумма квадратов остатков для модели порядка q. Вычисляется величина

,

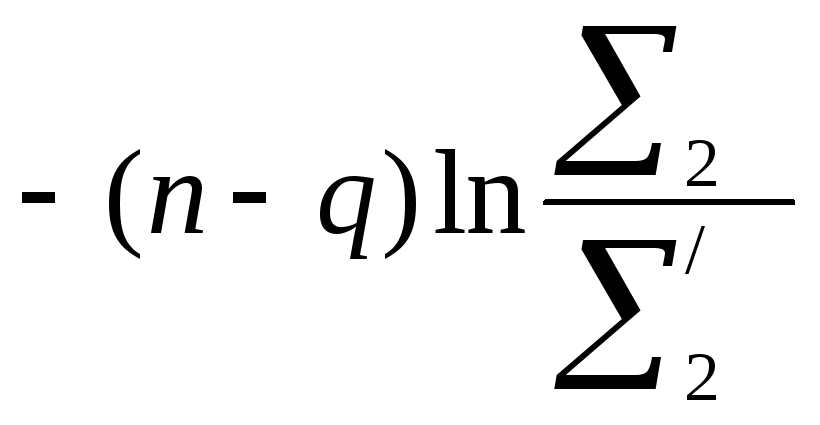имеющая распределение χ²c(q - p) степенями свободы. Таким образом, задав определенный уровень значимости, можно проверить гипотезу о том, что исследуемый процесс действительно представляет собой авторегрессию заданного порядка. Если расчетное χ² больше табличного, то процесс лучше аппроксимируется моделью порядка q. Если наоборот, то гипотеза о том, что авторегрессионная модель порядка q дает лучшие результаты, отвергается.

Итак, для описания динамики исследуемого процесса с помощью авторегрессионных моделей необходимо выполнить ряд последовательных процедур:

1) исключить тренд и сезонные колебания;

2) проверить ряд остатков на стационарность;

3) определить порядок модели авторегрессии;

4) оценить параметры модели;

5) дать экономическую интерпретацию модели и осуществить прогнозирование (см. п. 5.3).

Эти процедуры могут повторяться неоднократно в процессе уточнения модели.