Рассмотренный пример позволяет сделать несколько замечаний.

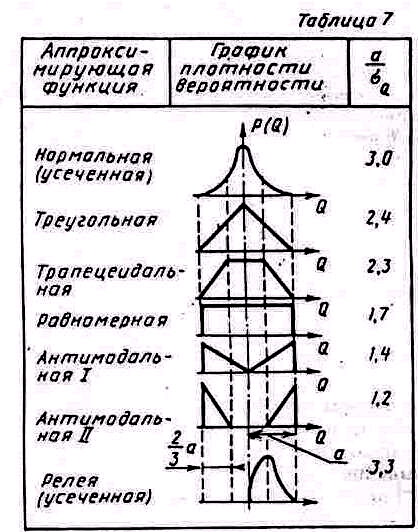
Замечание 1. Получение результата измерения служит промежуточным этапом, на котором измерительная информация должна представляться в форме, удобной для ее дальнейшей обработки (переработки). Такой формой является представление результата измерения с помощью числовых характеристик закона распределения вероятности. При однократном измерении чаще всего используется такая числовая характеристика закона распределения вероятности, как среднее квадратическое отклонение (или его аналог). С ее помощью определяются пределы, в которых находится значение измеряемой величины, осуществляется внесение поправки, точное значение которой неизвестно. Если пользоваться стандартными аппроксимациями законов распределения вероятности, представленными в табл. 7, то переход к этой числовой характеристике удобно осуществлять с помощью коэффициентов, приведенных в третьей графе.

3амечание 2. Цель измерения состоит в уточнении значения измеряемой величины. Если измерительная информация не предназначена для дальнейшей обработки (переработки), то она должна быть представлена в форме, удобной для восприятия человеком. Такой формой является указание пределов, в которых находится значение измеренной величины. Не рекомендуется пользоваться записью , так как в силу особенностей человеческой психики при этом возникает некоторая доминанта, акцент на середину интерва-

ла, для чего нет никаких оснований. Все значения Q в интервале равноправны.

Замечание 3. Внесение поправки, точное значение которой неизвестно, с одной стороны смещает интервал, в пределах которого находится значение измеряемой величины, а с другой – расширяет его. Из рассмотрения рис. 29 следует, что внесение неточно известной поправки целесообразно только тогда, когда

.

Замечание 4. касается достоверности измерений. Под достоверностью понимается степень доверия к тому, что значение измеренной величины находится в указанном интервале. Рассмотрим два случая, чаще всего встречающиеся на практике.

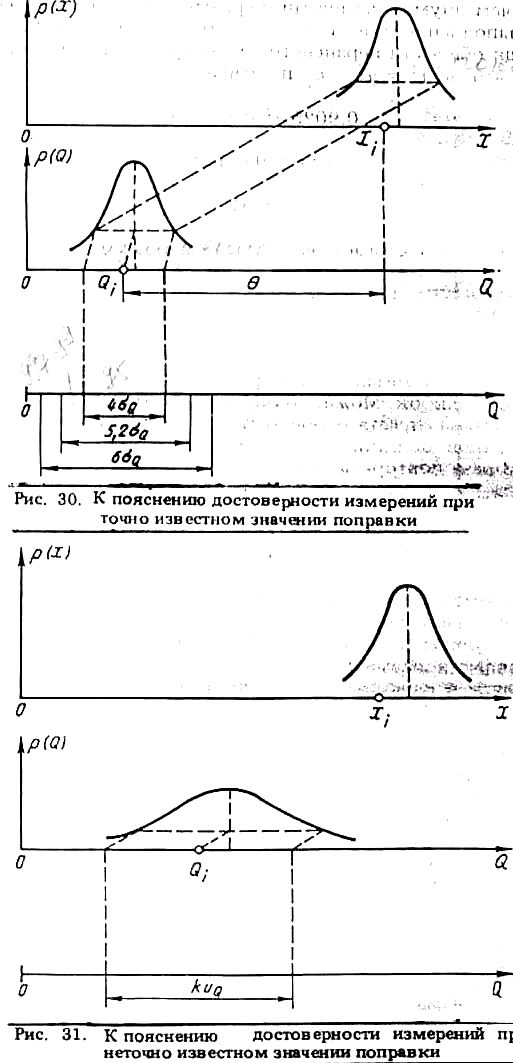
1. Результат измерения подчиняется нормальному закону распределения вероятности (см., например вариант 1), что бывает чаще всего при точно известном значении поправки. Точность результата измерения (см. рис. 30) в этом случае равна точности показания, которая в свою очередь характеризует точность средства измерений. Ширина интервала, в котором устанавливается значение измеряемой величины, зависит от выбранной доверительной вероятности. Чем выше эта вероятность, тем с большей гарантией, с большей достоверностью устанавливается значение измеряемой величины.

С вероятностью 0,95

,

С вероятностью 0,99

,

с вероятностью 0,997

.

Таким образом, в рассматриваемом случае доверительная вероятность является мерой достоверности измерений.

2. Результат измерения описывается композицией закона распределения вероятности показания и ситуационной модели, учитывающей неточность значения поправки (рис. 31). Достоверность измерений в этом случае обеспечивается выбором коэффициента k.

Замечание 5 связано с правилами округления. В метрологии принято среднее квадратическое отклонение или его аналог выражать одной значащей цифрой, например, 8; 0,5; 0,007. Две значащие цифры, например, 27; 0,016 удерживаются при особо точных измерениях и в тех случаях, когда значащая цифра старшего разряда меньше 4 (в промежуточных вычислениях сохраняется на одну значащую цифру больше). Вследствие этого, при квадратичном суммировании

любым из слагаемых под радикалом можно пренебречь, если его учет почти не меняети. Строго говоря, и при этом может уменьшиться до и', но так как значение u выражается не более чем двумя значащими цифрами, то условие можно считать выполненным, если и — u' < 0,05 u, откуда 0,95 и < и' . Возводя обе части неравенства в квадрат и принимая во внимание, что , получим

0,9025u² <u² – u_i²;

u_i² < 0,0975u²;

u_i < 0,312u.

Таким образом, слагаемым

всегда можно пренебречь. Это правило распространяется и на сумму нескольких слагаемых.

В п. 2.3.4 отмечалось, что при измерениях никто не застрахован от ошибок. Может оказаться ошибочным и единственное значение отсчета х_i, при однократном измерении. Во избежание такой ошибки однократное измерение рекомендуется 2 ... 3 раза повторить без совместной обработки полученных результатов.

2.6. МНОГОКРАТНОЕ ИЗМЕРЕНИЕ С РАВНОТОЧНЫМИ ЗНАЧЕНИЯМИ ОТСЧЕТА

Многократное измерение одной и той же величины пос­тоянного размера производится при повышенных требова­ниях к точности измерений. Такие измерения характерны для профессиональной метрологической деятельности и вы­полняются в основном сотрудниками государственной и ве­домственных метрологических служб, а также при тонких научных экспериментах. Это сложные, трудоемкие и дорого­стоящие измерения, целесообразность которых должна быть всегда убедительно обоснована. Один из создателей теории информации Л. Бриллюэн в статье "Теория информа­ции и ее приложение к фундаментальным проблемам физики” привёл „ слова Д. Габора о том, что "ничто не дается да­ром, в том числе информация". В полной мере это относится и к измерительной информации.

Результат многократного измерения описывается выраже­нием (6)(), приведенным в разд. 2.1. Как и результат однократ­ного измерения, он является случайным значением измеряемой величины, но его дисперсия

(11)

в п раз меньше дисперсии результата измерения Q. Благодаря такому обстоятельству, как это видно, например, на рис. 32, где выделены интервалы, соответствующие доверительной вероятности 0,95, точность определения значения измеряемой величины повышается в раз.

На рис. 32 показан случай, когда результат многократ­ного измерения - среднее арифметическое значение резуль­тата измерения — подчиняется нормальному закону распре­деления вероятности. Так бывает всегда, когда нормальному закону распределения вероятности подчиняется сам резуль­тат измерения Q. Наличие массива экспериментальных дан­ных

;

позволяет получить апостериорную информацию о законе распределения вероятности результата измерения. В частнос­ти, может быть поставлена задача его определения. Но чаще ограничиваются проверкой нормальности закона распределе­ния вероятности результата измерения и жертвуют точнос­тью при отрицательных результатах проверки.

Другой возможностью, которая открывается благодаря наличию большого объема экспериментальных данных, явля­ется обнаружение и исключение ошибок по правилу "трех сигм". Таким образом, специфическая особенность много­кратного измерения состоит в эффективном использовании апостериорной измерительной информации.

Последнее вовсе не означает, что необходимость в анали­зе априорной информации отпадает. Такой анализ обязатель­но предшествует многократному измерению и преследует те же цели, что и при однократном измерении, но с той разни­цей, что при многократном измерении информация о законе распределения вероятности результата измерения получает­ся опытным путем.

Вслед за анализом априорной информации и тщательной подготовкой к многократному измерению получают п неза­висимых значений отсчета. Эта основная измерительная проце­дура может быть организована по-разному. Если изменением измеряемой величины по времени можно пренебречь, то все значения отсчета проще всего получить путем многократного повторения операции сравнения (2) с помощью одного и того же средства измерений. Отсчет в этом случае будет описываться эмпирической плотностью распределения вероятности р(x₁, x₂, … , х_i, . . . , х_n) — см. пример 4, где согласно основно­му постулату метрологии каждое значение отсчета является случайным числом, подчиняющимся этому закону распреде­ления вероятности. Такие значения отсчета х_i, имеющие оди­наковую дисперсию, называются равноточными. Если же из априорной информации следует, что за время измерения про­изойдет существенное изменение измеряемой величины, то ее измеряют одновременно несколькими средствами изме­рений, каждое из которых дает одно из независимых значе­ний отсчета x_i. Так как средства измерений могут отличать­ся по точности, то в эмпирической плотности распределения вероятности отсчета Р (х₁, х₂, ..., х_i,..., х_n) случайные чис­ла x_i могут иметь разную дисперсию. Такие значения отсчета x_i называются неравноточными. Многократное измерение с неравноточными значениями отсчета, рассматривается в следующем разделе.

Порядок выполнения многократного измерения с равно­точными значениями отсчета показан на рис. 33.

Все значения отсчета x_i, независимо от способа их полу­чения, переводятся в показания Х_i, в которые вносятся поп­равки . Если многократное измерение выполняется од­ним средством измерений, то поправки могут отличаться друг от друга из-за изменения во времени влияющих факторов. Если же используются одновременно несколько средств из­мерений, то поправки отличаются из-за индивидуальных осо­бенностей каждого из них. Для простоты будем считать их из­вестными точно.

Полученный массив экспериментальных данных может содержать ошибки. Причины появления ошибок и "правило трех сигм", которым пользуются для их выявления, рассмотрены в разд. 2.3.4. Для того, чтобы воспользо­ваться этим правилом, нужно знать числовые харак­теристики закона распределения вероятности результата измерения — среднее значение и среднее квадратическое от­клонение. Однако, как уже отмечалось в разд. 2.2, 2.4, вычислить их невозможно из-за конечного п и практической нереализуемости интегрирования в бесконечных пределах. Можно лишь как-то оценить эти числовые характеристики на основе ограниченного экспериментального материала, указать их приближенные значения или пределы, в которых они на­ходятся с определенной вероятностью.

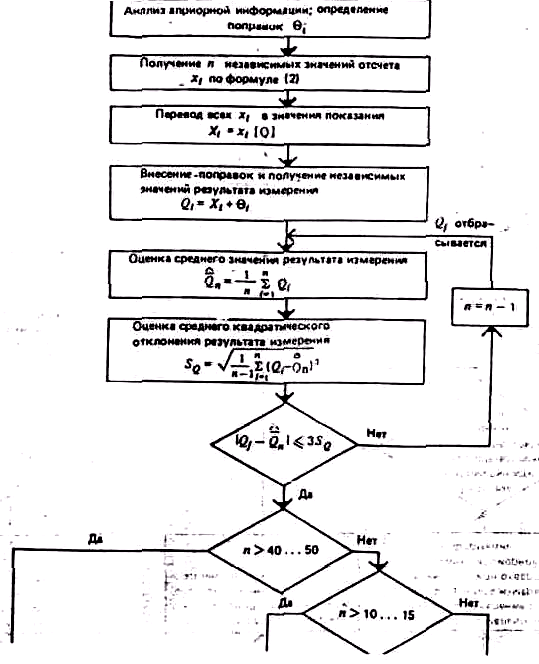
Рис. 33. Порядок выполнения многократного измерения при равноточных значениях отсчета