Чтобы обеспечить запас устойчивости для сжатого стержня, нужно, чтобы действующая сжимающая сила не превышала допускаемой величины, определяемой по формуле:

,(14.1)

где  коэффициент запаса устойчивости.

Следовательно, чтобы произвести расчет сжатого стержня на устойчивость, нужно уметь определять для него величину критической силы.

14.2. Вывод формулы Эйлера для определения критической силы сжатого стержня

Задача определения критической силы для сжатого стержня впервые была решена в 1744 году выдающимся математиком Леонардом Эйлером. Швейцарец по происхождению, Леонард Эйлер большую часть своей жизни прожил в России, был действительным членом Петербургской академии наук, написал около 850 научных работ, посвященных вопросам астрономии, физики, математики и механики.

Метод Эйлера основан на анализе разветвления возможных форм равновесия упругой системы. Рассмотрим его идею более подробно на примере центрально сжатого, идеально прямого стержня. При малых сжимающих силах прямолинейная форма стержня является устойчивой. При больших силах, превышающих некоторое критическое значение, она является неустойчивой, а устойчивой будет криволинейная форма.

Таким образом, при теоретически возможно существование двух форм равновесия.Наименьшее значение сжимающей силы, при котором наступает разветвление форм упругого равновесия, и называется критической силой. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма.

Для вывода формулы Эйлера рассмотрим прямой стержень постоянного сечения, шарнирно опертый по концам (Рис.14.2). Одна из опор стержня допускает возможность продольного перемещения соответствующего конца стержня. Собственным весом стержня будем пренебрегать.

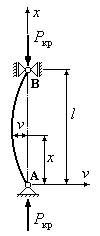
Рис.14.2

Нагрузим стержень центрально приложенными продольными сжимающими силами и дадим ему весьма небольшое искривление в плоскости наименьшей жесткости. Стержень удерживается в искривленном состоянии. Это возможно, так как. Деформация изгиба стержня предполагается весьма малой, поэтому для решения поставленной задачи воспользуемся приближенным дифференциальным уравнением изогнутой оси стержня. Выберем начало координат в точке А и направление осей координат, как показано на рис.14.2. Дифференциальное уравнением изогнутой оси стержня имеет вид:

. (14.2)

Вычислим изгибающий момент в сечении , взятом на расстоянииот начала координат:

. (14.3)

В формуле (14.3) знак “” взят потому, что ордината является отрицательной. Если бы стержень искривился выпуклостью право, изгибающий момент был бы положительным при положительном прогибе, а общий результат отрицательным, так как кривизна изогнутого стержня в выбранной системе координат была бы отрицательной. В этом случае перед положительным моментом проставляется знак“” (Тема №6, формула (6.5)).

Подставим (14.3) в (14.2), получим:

. (14.4)

В формуле (14.4) взят минимальный момент инерции , так как очевидно, что прогиб произойдет перпендикулярно оси наименьшей жесткости, если на концах стержня шаровые шарниры.

Деля обе части уравнения (14.4) на минимальную жесткость и обозначая дробь, приводим уравнение (14.4) к виду:

. (14.5)

Общий интеграл этого уравнения имеет вид:

. (14.6)

Это уравнение заключает в себе три неизвестных: А, В и значение , так как величина критической силы нам неизвестна.

Сначала найдем постоянные интегрирования А и В из граничных условий  условий поведения стержня на опорах. Таких условий два: на опоре А при прогиб. Подставляя эти значения продольной координаты и соответствующий прогиб в уравнение (14.6), получим:

, откуда находим .

Уравнение (14.6) приобретает вид:

. (14.7)

Таким образом, сжатый стержень, выпучиваясь, искривляется по синусоиде.

Для определения второй постоянной интегрирования А воспользуемся вторым граничным условием: на опоре В при прогиб.

Подставляя значение продольной координаты и прогиб в сечении В в уравнение (14.7), имеем:

. (14.8)

Из уравнения (14.8) следует, что либо постоянная , либо нулю равняется.

Если коэффициент А будет равен нулю, то из уравнения (14.7) следует, что прогиб в любом сечении стержня равен нулю, т.е. стержень не будет выпучиваться, оставаясь прямым. Это противоречит исходным предпосылкам о поведении стержня. Следовательно, постоянная интегрирования . Нулю будет равняться. Это возможно, когда аргумент функцииприобретает бесконечный ряд значений:

, (14.9)

где  любое целое число. Исключая из числа аргументов значение , получим. А так как, величина критической силы для стержня равняется:

. (14.10)

Таким образом, нагрузка способная удержать слегка искривленный стержень в равновесии, теоретически может иметь целый ряд значений. С практической точки зрения наиболее важным является наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб. Это значение сжимающая сила будет иметь при .

Если взять первое значения корня , то это будет означать, что критическая силатакже будет равна нулю, а это противоречит условию задачи. Значит, этот корень отбрасывается и принимается в качестве наименьшего значение. Тогда критическая сила принимает вид:

. (14.11)

Формула (14.11) называется формулой Эйлера для критической силы сжатого стержня с шарнирно-опертыми концами. Значению силы (14.11) соответствует изгиб стержня по синусоиде с одной полуволной (14.7):

. (14.12)

Значениям критической силы высших порядков соответствует искривление по синусоидам с двумя, тремя и т.д. полуволнами (Рис.14.3):

. (14.13)

Таким образом, чем больше точек перегиба будет иметь синусоидально-искривленная ось стержня, тем большей должна быть критическая сила. Более полные исследования показывают, что формы равновесия, определяемые формулами (14.13), неустойчивы. Они переходят в устойчивые формы лишь при наличии промежуточных опор в точках В и С (Рис.14.3).

Рис.14.3

Величина постоянной интегрирования осталась неопределенной. Физический смысл выяснится, если определим максимальный прогиб(стрелу прогиба), воспользовавшись уравнением (14.12). Максимальный прогибпри. Тогда.

Следовательно, общий вид уравнения упругой линии сжатого стержня имеет вид:

. (14.14)

Координату сечения , в котором возникнет максимальный прогиб, найдем, взяв первую производную от функции прогибапо продольной координатеи приравняв ее нулю:

т.е. или.

Наименьшее значение аргумента, при котором косинус равен нулю, будет , значит:

, откуда . (14.15)

Если , то, а максимальный прогиб возникнет посредине стержня, что соответствует основному случаю (Рис. 14.1,б). Координаты сечений, в которых возникнет максимальный прогиб прии, соответственно равныи(Рис.14.3). Как следует из соотношения (14.13) и рис.14.3, числопредставляет собой число полуволн синусоиды, располагающейся на длине изогнутого стержня.

14.3. Влияние способов закрепления концов стержня на величину критической силы

Формула Эйлера (14.11) для критической силы выводилась для стержня с шарнирным закрепление концов. Этот случай закрепления концов стержня принято называть основным случаем. В этом случае на длине стержня укладывается одна полуволна синусоиды. Между тем, в практике встречаются различные другие случаи опирания концов стержня. На рис.14.4 приведены некоторые из них, наиболее часто встречающиеся. Значение критической силы для каждого из приведенных случаев закрепления концов, очевидно, можно вывести, так же, как и формулу Эйлера, интегрируя приближенное дифференциальное уравнение упругой линии, но при других граничных условиях. Однако на практике применяется более простой способ определения величины критической силы, использующий геометрическую аналогию между поведением упругой линии сжатого стержня с шарнирным закреплением концов (основной случай) и иным способом опирания концов стержня. По этому способу все остальные случаи закрепления концов стержня приводятся к основному путем введения так называемой приведенной или свободной длины стержня.

Приведенной или свободной длиной стержня называется условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как и стержень с заданным закреплением концов. Судить о приведенной длине стержня можно по числу полуволн, которые укладываются на длине стержня. Из геометрической аналогии следует, что в пределах приведенной длины стержень с произвольным закреплением концов будет вести себя так же, как стержень с шарнирным опиранием концов. Впервые понятие приведенной или свободной длины было введено профессором Петербургского института путей сообщения Ф.С.Ясинским.

Рис.14.4

Приведенная длина стержня вычисляется следующим образом: , где длина стержня с заданным опиранием концов;  коэффициент приведенный длины.

Из определения приведенной длины следует, что коэфиициент есть некоторое число, на которое нужно умножить длину стержня с заданным закреплением концов, чтобы получить такую длину условного стержня, на котором уляжется одна полуволна синусоиды (14.7).

Для стержня, изображенного на рис.14.4,а длина условного стержня должна быть в два раза больше заданной длины стержня. Верхняя часть условного стержня с шарнирным опиранием концов будет вести себя точно так же, как стержень с заданным закреплением концов. Коэффициент приведения длины для этого случая принимается . На рис.14.4,в одна полуволна поместится на длине, составляющей 0,7 реальной длины стержня. Коэффициент приведения длины в этом случае составляет. Для случая жесткого опирания обоих концов стержня (Рис.14.4,г) длина полуволны, замеренная между двумя точками перегиба, составит половину длины стержня. Для этого случая коэффициент. Для основного случая (Рис.14.4,б) коэффициент, так как на его длине ложится одна полуволна и, следовательно, приведенная длина стержняравна реальной его длине.

Для других случаев закрепления концов стержня значения коэффициентов приведения длины стержня приведены в специальной справочной литературе [3].