Оулы 1-3

3)	x2 y2	10x 9 0 шеңберлерін салыңыз.
Шешуі: 1) Шеңберді салу үшін берілген теңдеудің толық квадрат
формуласын	( a b 2	a2 2ab b2 )	пайдалана отырып, жалпы	түрге
келтіреміз, ол үшін ең алдымен айнымалыларды топтастырамыз, яғни
		x2 6x y2	2y 1 0	(5.34)

теңдеуін аламыз. Осы теңдеудегі әрбір айнымалыны толық квадратқа келтіру үшін мына түрлендірулерді қолданамыз:

a2 x2 a x, 2ab 6x 2xb 6x b 3

онда b2 9, сондықтан бірінші жақшадағы өрнек

x2 6x x2 6x 9 9 x 3 2 9

түрінде жазылады, ал

a2 y2 a y, 2ab 2y 2yb 2y b 1

онда b2 1, сондықтан екінші жақшадағы өрнек

	y2 2y y2 2y 1 1 y 1 2 1
түрінде жазылады. Сонымен (5.34) теңдеуі мына түрде жазылады
x 3 2 9 y 1 2 1 1 0 x 3 2 y 1 2 9,
яғни центрі O(3; 1)	нүктесінде орналасқан, радиусы R 3 тең шеңбер аламыз
(29-сурет).	y
		3
	1	x
		R

29-сурет Дәл осылай 2) және 3) теңдеулермен берілген шеңберлерді де салуға

болады.

y	y
4R	R

0 x

5

0 x

30-сурет 31-сурет

2) x2 y2 8y 12 0 x2 y2 8y 12 0

x2 y2 8y 16 16 12 0 x2 y 4 2 16 12 x2 y 4 2 4,

яғни центрі O(0;4) нүктесінде орналасқан, радиусы R 2 болатын шеңбер аламыз (30-сурет).

3) x2 y2 10x 9 0 x2 10x y2 9 0

96

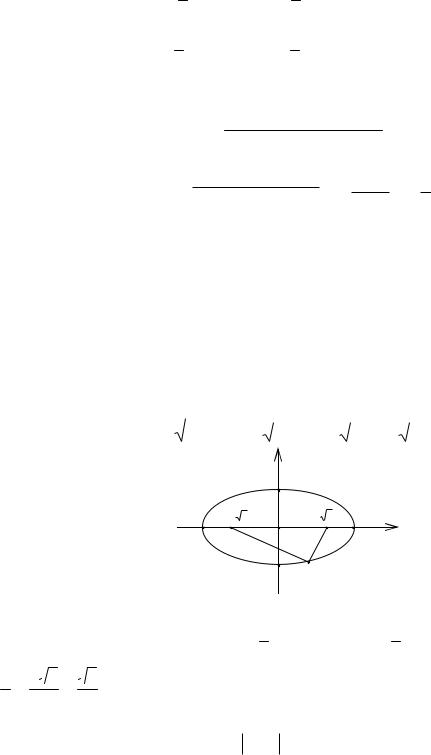
x2 10x 25 25 y2 9 0 x 5 2 y2 9 25 0 x 5 2 y2 16,

яғни центрі O( 5;0) нүктесінде орналасқан, радиусы R 4 болатын шеңбер аламыз (31-сурет).

3-есеп. A1;2 және B 3;2 нүктелері берілген. AB кесіндісі диаметр болатындай шеңбер теңдеуін жазыңыз.

Шешуі: Бұл есепте AB диаметрі арқылы шеңбердің центрін табамыз. Ол үшін кесіндіні теңдей екі бөлікке бөлу формуласы бойынша O-нүктесінің координаталарын табамыз:

	x				x1 x2			x			3 1		2	;
2							2
y				y1 y2				y		2 2			2		,
2							2

яғни центрі O 2;2 нүктесі болады. Бұдан OA шеңберінің радиусын табамыз. Ол екі нүктенің арақашықтығын есептеу формуласы

d x2 x1 2 y2 y1 2

бойынша есептелінеді. Яғни

R OA 3 1 2 2 2 2 4 0 4 2

тең. Сонымен ізделінді шеңбер теңдеуі мына түрде жазылады

x 2 2 y 2 2 4.

4-есеп. x2 4y2 16 теңдеуімен берілген эллипстің фокустары мен эксцентриситетін табыңыз және сызбасын салыңыз.

Шешуі: Берілген теңдеуді эллипстің канондық теңдеуіне келтіреміз:

x2 4y2 16

x2

y2

1 a 4, b 2

онда

16

4

c

2

a2 b2

16 4

12

3

y

B1 0,2

A1 4,0 F1 2

3;0

F2 2

3;0

A2 4,0

0

r2

x

r

1

B 0, 2

M x,y

2

32-сурет

болады. Демек фокустары F1 23;0 және F2 23;0 , ал эксцентриситеті

c 2 3 3 болатын эллипс аламыз (32-сурет). a 4 2

5-есеп. Берілгені:

1) фокустарының арақашықтығы F1F2 8, ал кіші жарты өсі b 3 болатын;

97

2) үлкен жарты

өсі a 6, ал эксцентриситеті

0,5

болатын

эллипстің

канондық теңдеуін жазып көрсетіңіз.

Шешуі: 1) 5.2.1 бөлімде көрсетілгендей F1( c; 0) және

F2( c; 0)

болатындықтан

F1F2

2c. Онда есептің шарты бойынша 2с 8 с 4, ал

b 3

тең, онда

c2

a2 b2

a2 c2 b2

16 9 25 a 5. Сондықтан

эллипстің канондық теңдеуі мына түрде жазылады

x2

y2

1.

c

25

9

2)

5.2.3 бөлімінен

болатындықтан,

есептің шарты

бойынша

a

c

0,5,

ал

a 6

тең,

онда c 0,5 6 3

болады.

Сонда

c2 a2 b2

a

b2 a2

c2

36 9 27 b

тең.

Демек эллипстің канондық теңдеуі

27

мына түрде жазылады

x2

y2

1.

6-есеп. Эллипстің үлкен

36

27

a 5

1) 4,8;

2) 4;

жарты

өсі

және

саны белгілі болғандағы

3) 3;

4)1,4;

5)0 мәндеріне тең

c

a2 b2

кіші

жарты өс b мен эксцентриситет -нің мәндерін табыңыз.

Шешуі: 1) a 5, с 4,8 онда

c2

a2 b2 b

с

a2 b2

a2 c2

1,4,

25 23,04

яғни b 1,4,

ал

c

демек

4,8

24

тең.

a

5

25

2) a 5, с 4, с a2 b2 c2 a2 b2 b a2 c2 25 16 3,

c 4 . a 5

3) a 5, с 3, с a2 b2 c2 a2 b2 b a2 c2 25 9 4,

c 3. a 5

4) a 5, с 1,4, с a2 b2 c2 a2 b2 b a2 c2 25 1,96 4,8,

	c		1,4		7	.
	a
		5		25

5) a 5, с 0, с 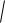a2 b2 c2 a2 b2 b a2 c2 25 0 5,

c 0 0. a 5

7-есеп. x2 4y2 16 гиперболасы мен оның ассимптоталарын салыңыз. Шешуі: Берілген теңдеуді гиперболаның канондық теңдеуіне келтіреміз:

98

x2 4y2

16

x2

y2

1,

сонда

a 4,

b 2,

y

b

x

1

x

болады (33-

сурет).

16

4

a

2

y

y

1

x

y

1

x

2

2

2

M x;y

2 5;0

r1

r2

F1

F2 2

5;0 x

4

2

4

8-есеп. x2 4y2 16

33-сурет

тең M k;1

гиперболасынан

ординатасы

1-ге

нүктесі алынған. Осы M нүктесінен гипербола фокустарына дейінгі арақашықтықты табыңыз.

Шешуі: Берілген теңдеуді гиперболаның канондық теңдеуіне келтіреміз:

	x2 4y2 16					x2							y2																			c																							2
																	1,				a 4, b 2,														a2 b2
																																										16 4											20						5
					16						4								F1 2								5;0									F2 2			5;0
	тең,	демек	фокустары																													және															(33-сурет), ал
														c				2
	эксцентриситеті																			5						5				болады.						Берілген								M k;1									нүктесі
																			4
														a							2										x2			y2				k2														k2
																																				1							1				1									5
	гиперболада		жататын														болғандықтан
																																						16					4								16					4
																														16			4
	k2 20 k 2							,			яғни M 2													5;1			тең. Енді осы нүктеден																	F 2							5;0					және
					5
	F2 2	5;0																																									1
			фокустарына																	дейінгі										арақашықтықты													5.3.1								бөлімінде
	көрсетілгендей								сәйкес											F1M r1 a x																және						F2M r2											a x
	формулаларымен										анықтаймыз,																сонда						FM r 4											5			2			9						және
																																																	5
																																	1			1		2
	F M r 4						5			2					1				болады.											Ал,		осы арақашықтықтың дұрыстығын
													5
	2	2			2

тексеру үшін жазықтықтағы екі нүктенің арақашықтығын есептеу формуласын қолданамыз, яғни A x1,y1 және B x2,y2 болса, онда

AB x2 x1 2 y2 y1 2

орындалады. Демек, осы формула бойынша

F1M 25 2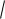5 2 1 0 2 9

және

F2M 25 25 2 1 0 2 1

болады.

99

9-есеп. Берілгені:

1) фокустарының арақашықтығы 2c 10, ал төбелерінің арақашықтығы 2a 8 болатын;

2) нақты жарты осі a 25, ал эксцентриситеті 1,2 болатын гиперболаның канондық теңдеуін жазыңыз.

Шешуі: 1) Берілгені бойынша 2c 10 c 5, 2a 8 a 4 болады, онда

c2 a2 b2 b2 c2 a2 25 16 9 b 9

тең, демек гиперболаның канондық теңдеуі

										x2			y		2	1
болады.								16					9
				c
2) a 2									c					2				2					,
							1,2					1,2					5		6			24
		5,
				a
c2 a2 b2	b2 c2					a2		25 16 9 b 9, демек
										x2			y		2	1
болады.								20					4
		F 0;2										y 4
10-есеп.						нүктесі мен											түзуінен				бірдей арақашықтықта

жатқан нүктелердің геометриялық орнының теңдеуін жазыңыз. Бұл сызықтың координата өстерімен қиылысу нүктелерін табыңыз және сызбасын салыңыз.

Шешуі: Алдымен F 0;2 нүктесі мен

y 4 түзуінің Oy өсі

(x 0)

бойындағы ортасын табамыз. Ол нүктені A

,

деп белгілесек, онда

x

y

0 0

0 және

2 4

3,

x

y

яғни A 0;3 болады.

2

2

Онда есептің

шарты бойынша ізделінді нүктелердің

геометриялық орны симметрия өсі

Oy және бас нүктесі A 0;3 болатын

параболаны береді. 5.4.3 бөлімінде көрсетілген

x2 2py

(p 0)

фомуласының негізінде, егер параболаның бас нүктесі

A x0,y0 болса,

онда

x x0 2

2p y y0

формуласын

аламыз.

Берілген

y 4 түзуінің

Oy

өсімен

қиылысу

нүктесін

D 0;4

деп

белгілесек

онда

p FD 0 0 2 4 2 2 2. Сондықтан

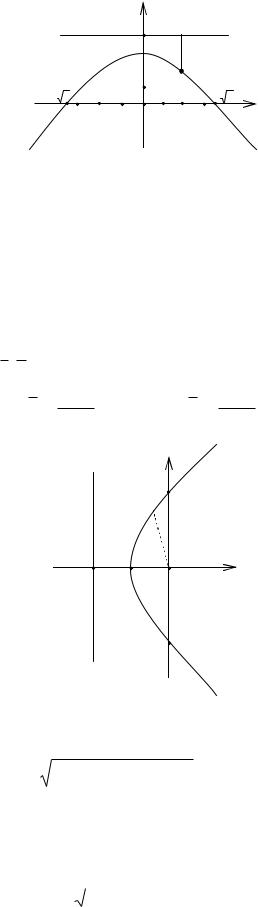
x 0 2 2 2 y 3 x2 4 y 3

параболасын аламыз (34-сурет). Осы параболаның координата өстерімен қиылысу нүктелерін табамыз:

x 0 4 y 3 0 4y 12 0 4y 12 y 3;

y 0 x2 12 x 12 x 23, яғни x1 23 және x2 23 (34-

сурет).

100

y

y 4

A 0;3

F 0;2 M x, y

2 3

2 3

x

34-сурет

11-есеп. Координаталар бас нүктесінен және x 4 түзуінен бірдей қашықтықта жатқан нүктелердің геометриялық орнының теңдеуін жазыңыз. Алынған сызықтың координата остерімен қиылысу нүктелерін табыңыз және сызбасын салыңыз.

Шешуі: Алдыңғы есепте айтылғандай іздеп отырған сызығымыз фокусы координаталар бас нүктесі F 0;0 және директрисасы x 4 түзуі болатын Ox өсіне қарағанда симметриялы болатын парабола болады. Осы параболаның бас нүктесін табу үшін F 0;0 нүктесі мен x 4 түзуінің ортасы болатын A x, y нүктесін табамыз:

x 0 4 2 және y 0 0 0,

2 2

y

4

Mx;y

x4

D 4;0	A 2;0	F 0;0
4		x

4

35-сурет

яғни A 2;0 болады. Енді параболаның параметрін табу үшін, формуланы

қолданамыз p		FD				4 0 2	0 0 2	4,	мұндағы	D 4;0	нүктесі
x 4 түзуінің			Ox			өсімен	қиылысу		нүктесі.	Онда	парабола
y2 2 4 x 2 y2			8 x 2 теңдігімен					анықталады		(35-сурет). Бұл

параболаның координата өстерімен қиылысу нүктелері мына түрде табылады:

x 0 y2 16 y	16	y 4, яғни y	4 және	y	2	4;
	1

y 0 0 8 x 2 8x 16 0 8x 16 x 2 (35-сурет).

101

12-есеп. 1) O 0;0 және A1; 3 нүктелері арқылы өтетін және Ox-ке қарағанда симметриялы орналасқан;

2) O 0;0 және B 2; 4 нүктелері арқылы өтетін және Oy-ке қарағанда симметриялы орналасқан парабола теңдеуін жазыңыз.

Шешуі: 1) Есептің шарты бойынша парабола Ox-ке қарағанда симметриялы болғандықтан, оның бас нүктесі O 0;0 болады және A1; 3 нүктесі параболада жататын болғандықтан оның тармағы Ox өсінің оң

жағында болады, яғни параболаның			жалпы теңдеуі у2 2px түрінде
жазылады. Берілген A1; 3		нүктесі	параболада	жатады,	сондықтан
9 2р 1 2р 9 р 4,5	онда у2 9х болады.
2) Парабола Oy-ке қарағанда симметриялы болғандықтан оның бас
нүктесі O 0;0 болады	және	B 2; 4 нүктесі		параболада	жататын

болғандықтан оның тармағы Oy өсінің теріс жағында болады, яғни параболаның жалпы теңдеуі x2 2py түрінде жазылады. Берілген B 2; 4 нүктесі параболада жатады, сондықтан 4 2р 4 2р 1 р 0,5 онда x2 y болады.

VІ. Екінші ретті беттер туралы жалпы ұғымдар

6.1 Бет теңдеуі

Аналитикалық геометрияда кезкелген бетті кеңістіктегі нүктелердің геометриялық орны деп қарастырамыз. Беттің осы анықтамасында сол бетке тиісті нүктелердің барлығына ортақ қасиет қамтылады.

Тікбұрышты координаталар жүйесіндегі беттің кез келген нүктесінің координаталарын x, y, z-деп белгілесек, онда олардың арасындағы байланыс арқылы бет нүктелерінің қасиетін өрнектейтін теңдеу құрамыз. Мұндай теңдеу бет теңдеуі, ал оны қанағаттандыратын координаталар – x, y, z тер ағымдағы координаталар деп аталады.

Сонымен осы түрде құрылған теңдеулер арқылы беттердің геометриялық қасиеттерін, олардың сәйкес аналитикалық қасиеттері арқылы зерттейміз.

Берілген беттің теңдеуін құрудың классикалық мысалы ретінде тікбұрышты координаталар жүйесінде центрі C a, b, c нүктесінде болатын және радиусы R ге тең сфераның теңдеуін құрамыз. Ол үшін сфераның кез келген M нүктесінің координаталарын x, y, z деп алып, оның барлық нүктелеріне ортақ аналитикалық қасиеттерін өрнектейміз. Сфераның анықтамасы бойынша оның кезкелген M нүктесінің центрінен қашықтығы әрқашан тұрақты және оның радиусына тең, яғни

CM R.

(6.1)

Екі нүктенің арақашықтығының формуласынан

102

CM x a 2 y b 2 z c 2 .

Ендеше (6.1) теңдеуі

CM 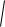x a 2 y b 2 z c 2 R

түрінде немесе
x a 2 y b 2 z c 2 R2	(6.2)

түрінде жазылады. Осы (6.2) теңдеуін сфераның теңдеуі болып табылады. Дербес түрде, (6.2) теңдеуінде a b c 0 тең болғанда, яғни сфераның центрі координаталар жүйесінің бас нүктесінде орналасқанда, (6.2) теңдеуі

x2 y2 z2

R2

(6.3)

түріндегі қарапайым теңдеумен жазылады. Дәл осылай кез келген беттің барлық нүктелеріне ортақ қасиетті сол нүктелердің координаталары арқылы теңдеу түрінде жазуға болады, ол теңдеу жалпы түрде былай жазылады:

F x,	y, z 0.	(6.4)
Керісінше, осы (6.4) теңдеуі	жалпы алғанда,	айнымалылар x, y, z

арқылы жазылған бетті нүктелердің геометриялық орны ретінде анықтайтын болады. Осы жоғарыдағы айтылғандардан мынадай негізгі екі мәселені қортып шығарамыз:

1)бет нүктелердің геометриялық орны ретінде берілсе, онда осы беттің теңдеуін жазуымыз керек;

2) координаталар x, y, z ті байланыстыратын теңдеу берілсе, онда осы теңдеу арқылы анықталатын беттің кескінін зерттеуіміз керек.

6.2 Сфера

Центрі C a, b, c нүктесінде, ал радиусы R болатын сфераның теңдеуі

(6.2) екенін, яғни
x a 2 y b 2 z c 2			R2	(6.2)
болатынын білеміз.
Енді осы теңдеудегі жақшаларды ашып, теңдеуді
x2 y2 z2	2ax 2by 2cz a2	b2 c2 R2 0		(6.5)
түрінде жазамыз.	айнымалылар x,	y	және z ке
Соңғы теңдеуден				қарағанда

айнымалылары екінші, бірінші және нөл дәрежелі мүшелердің бар екендігін көреміз. Осы түрдегі теңдеуді екінші дәрежелі теңдеу деп есептейміз. Сонымен сфераның теңдеуі ағымдағы координаталарға қарағанда екінші дәрежелі теңдеу болатынын көреміз. Бірақ кезкелген түрдегі екінші дәрежелі теңдеу сфераны анықтай бермейді.

Шындығында (6.5) теңдеуінен сфераның теңдеуінде ағымдағы координаталардың квадраттарының коэффициенттері өзара тең екендіктерін, ал координаталарының көбейтінділері yx, xz, yz болмайтынын көреміз.

103

Керісінше, екінші дәрежелі жалпы теңдеуде, біріншіден x2, y2 және z2 тың коэффициенттері өзара тең болса, екіншіден, координаталарының көбейтінділері xy, xz, yz жоқ болатын болса, онда ол сфераны анықтайтын болады, яғни ондай теңдеуді әр уақытта (6.2) түріне келтіруге болатынын көреміз.

Сонымен, берілген екінші дәрежелі (ағымдағы x, y, z ке қарағанда) теңдеу арқылы оның сфераны анықтайтынын немесе анықтамайтынын көре аламыз.

Мысалы, x2 y2 z2 6y 4z 2 0 теңдеуінің сфераны анықтайтынын көрсетеміз.

Шешуі: Шындығында берілген теңдеуде x2, y2 және z2 тардың коэффициенттері өзара және бірге тең. Берілген теңдеуді түрлендіріп,

x 0 2 y 3 2 z 2 2 9 4 2 0

немесе

x 0 2 y 3 2 z 2 2 15

түріне келтірсек, онда центрі C 0, 3, 2 нүктесінде болатын, ал радиусы

R 15 ке тең сфера болатындығын көреміз.

6.3 Цилиндрлік беттер

1-анықтама. Берілген L сызығын қиятын және екінші берілген l түзуіне параллель түзулерден тұратын бет цилиндрлік бет деп аталады.

Мұндағы L түзуі цилиндрлік беттің бағыттаушысы, ал l түзуіне параллель түзулер оның жасаушылары деп аталады.

36-сурет	37-сурет
Жоғарыда келтірілген (6.4) түрінде берілген беттің жалпы теңдеуінде
айнымалы z жоқ болсын, онда (6.4) теңдеуі
F x,y 0	(6.6)

түрінде жазылады. Бұл теңдеу xOy жазықтығында қандай да бір L сызығын анықтайтын болады, яғни координаталары осы теңдеуді қанағаттандыратын нүктелердің геометриялық орны L сызығы болады (36-сурет). Бұл теңдеуді

104

абсциссасы мен ординатасы L сызығының кез келген нүктесінің кооридинаталарымен дәл келетін кеңістік нүктесінің координаталары да қанағаттандыратын болады, яғни xOy жазықтығына L сызығының нүктелеріне проекцияланатын кеңістік нүктелерінің координаталары қанағаттандырады. Oz өсіне параллель түзулерді құратын және L сызығын қиып өтетін кеңістіктің осындай нүктелерінің жиынтығынан бет құралатын болады.

Жалпы берілген l түзуіне параллель және берілген L сызығын қиятын түзулерден құрылған бет цилиндрлік бет деп, L сызығы – оның бағыттаушысы, ал бетті құрайтын түзулер оның жасаушысы деп аталатын болады.

Сонымен (6.6) теңдеуі жасаушысы Oz өсіне параллель цилиндрлік бетті анықтайды және керісінше, жасаушылары Oz өсіне параллель болатын цилиндрлік бет (6.6) теңдеуімен өрнектеледі.

Шындығында бұл жағдайда бағыттаушысы L сызығы xOy координат жазықтығында болады да, оның (6.6) теңдеуін кеңістікте қарастыратын болсақ, ол берілген цилиндрлік беттің де теңдеуі болып саналады. Сонымен, Oxyz кеңістігінде жасаушысы L сызығы болатын цилиндрлік бет

F x,	y 0
	(6.7)
z 0

теңдеулер жүйесі арқылы анықталады. Дәл осы сияқты егер теңдеуде айнымалы x немесе y жоқ болатын болса, онда ол теңдеу жасаушысы сәйкес түрде Ox немесе Oy өсіне параллель болатын цилиндрлік бетті

	анықтайтын болады.
	Цилиндрлік беттердің мысалдарын қарастырамыз:
	1.	x2		y2	1	(6.8)
		a2		b2

теңдеуімен анықталатын бет эллипстік цилиндр деп аталады. Оның жасаушылары Oz өсіне параллель, ал бағыттаушысы xOy жазықтығында жатқан, жарты өстері a және b болатын эллипс. Ал егер a b болса, онда бағыттаушысы шеңбер болады да, цилиндрлік бет тік дөңгелек цилиндр болады (37-сурет). Оның теңдеуі x2 y2 a2 болады.

	2.	x2		y2	1	(6.9)
		a2		b2

теңдеуімен анықталатын бет гиперболалық цилиндр деп аталады (38-сурет). Бұл беттің де жасаушылары Oz өсіне параллель, ал бағыттаушысы xOy жазықтығындағы нақты жарты өсі a және жорымал жарты өсі b болатын гипербола.

3.

y2 2px

(6.10)

105