Оулы 1-3

теңдеуімен анықталатын бет параболалық цилиндр деп аталады. Бұл беттің де жасаушылары Oz өсіне параллель, ал бағыттаушысы xOy жазықтығында жатқан парабола (39-сурет).

38-сурет 39-сурет

6.4 Конустық беттер

2-анықтама. Берілген L сызығын қиып және берілген қандайда бір P нүктесінен өтетін түзулерден тұратын бет конустық бет, ал берілген L түзуі конустық беттің бағыттаушысы, берілген P нүктесі оның төбесі және бетті құратын түзулер оның жасаушылары деп аталады.

Конустың бағыттаушы L сызығының теңдеуі

		F1 x,		y, z 0	,		(6.11)
		F x,		y, z 0
			2
ал оның	төбесі P x0,	y0, z0	нүктесінде болсын.				Конустың жасаушысы
P x0, y0,	z0 нүктесінен және бағыттаушының					N x,	y, z нүктесінен өтетін

түзу болғандықтан (40-сурет), оның екі нүкте арқылы өтетін канондық теңдеуі

	X x0		Y y0			Z z0		(6.12)
	x x0		y y0			z z0
Енді (6.11) және (6.12) теңдеулерінен					x, y, z			айнымалыларын жоятын

болсақ, онда осыдан шыққан теңдеу ізделініп отырған конустық беттің теңдеуі болады. Осылай алынған теңдеудің өте бір қарапайым қасиеті – оның

X x0, Y y0,	Z z0	айырымдарына	қарағанда	біртекті	теңдеу
болатындығы.
Шындығында алдымен конустың төбесі координат жүйесінің бас
нүктесінде x0	y0 z0	0 , ал X, Y, Z	конустың	кезкелген	нүктесінің

координаталары болсын. Демек олар конустың теңдеуін қанағаттандыратын болады. Конустың теңдеуіндегі X, Y және Z ті сәйкес түрде X, Y, Z ( -кезкелген көбейткіш сан) көбейтінділерімен ауыстыратын болсақ, одан теңдеу өзгермейді. Бұдан біз теңдеудің ағымдағы координаталарға қарағанда біртекті екендігін көреміз.

106

Ал егер конустың төбесі x0, y0, z0 нүктесінде болса, онда координат жүйесінің бас нүктесін конустың төбесіне көшіретін боламыз. Сонда конустың теңдеуі жаңа координаталарға, яғни X x0 , Y y0 және Z z0 айырымдарына қарағанда біртекті болады.

Мысал ретінде төбесі координаттық жүйенің бас нүктесінде жататын және бағыттаушысы

Z c
		2		Y2		(6.13)
X					1
				b2
a2
теңдеулерімен анықталатын Z c			жазықтығында жатқан,			жарты өстері a

және b болатын эллипс, конустық бетті қарастырайық. Бұл бет екінші ретті конус деп аталады.

Конуста жататын, өзіміздің қалауымызша алынған, M X, Y, Z нүктесін қарастырайық. Осы және бас нүкте арқылы өтетін және конустың

бағыттаушысын N X, Y,

Z нүктесінде

қиып өтетін OM жасаушысын

жүргізейік (40-сурет). OM жасаушысының теңдеуі

x 0

y 0

z 0

X 0

Z 0

немесе

Y 0

x

y

z

(6.14)

X

Y Z

болады. Бұл теңдеуден X c

x

,

Y c

y

тең.

z

z

40-сурет

41-сурет

Осы алынғандарды (6.13) теңдеулерінің екінші теңдеуіне қойып,

c2x2

c2y2

1

a2z2

b2z2

немесе

x2

y2

z2

0

(6.15)

a2

b2

c2

107

болатындығын көреміз. Осы алынған теңдеу – екінші ретті конустың теңдеуі. Бұл жерден егер a b болса, онда конустың бағыттаушысы z c

жазықтығында жатқан

z c

x2 y2 a2

теңдеулерімен анықталған шеңбер болады да, конус кәдімгі дөңгелек конусқа айналады. Бұл жағдайда оның теңдеуі

	x2		y2		z2	0
	a2		a2		c2
түрінде жазылатын болады.
6.5 Айналу беттері
Oyz жазықтығында жататын
	X 0					(6.16)
	F Y,			Z 0

теңдеулерімен анықталатын L сызығы берілген болсын.

Енді осы L сызығы Oz өсін айналатын болсын. Сонда қандай да бір бет шығатын болады. Осылай алынған бет айналу беті деп аталады (41-сурет). Осы айналу бетінің теңдеуін құру керек. Ол үшін M x, y, z нүктесі айналу бетінің қандай да бір кез келген нүктесі болсын делік. Енді осы нүкте арқылы өтетін және Oz өсіне перпендикуляр жазықтық жүргізейік. Сонда осы жазықтық Oz өсін және берілген L сызығын сәйкес K және N нүктелерінде қиып өтетін болады. Ал KN және KM кесінділері бір шеңбердің радиустары болып табылады. Сондықтан да KN KM. Бірақ KN кесіндісінің ұзындығы N нүктесінің Y ординатасының абсолют шамасына тең, яғни

KN Y , ал KM OP x2 y2

болады. Демек

немесе

Y

x2

y2

Y

x2

y2

тең. Сонымен бірге N нүктесінің апликаты

Z ,

M

нүктесінің апликатасы

z ке тең: Z z .

Ал N нүктесі (6.16)

теңдеуімен берілген

L сызығында жатқандықтан,

оның Y және Z координаталары (6.16) теңдеуін қанағаттандыратын болады.

Сондықтан Y

x2 y2

және

Z z

мәндерін

(6.16) теңдеулерінің

екіншісіне қоятын болсақ,

F

z 0

x2 y2

;

(6.17)

теңдеуін аламыз.

Осы алынған

(6.17)

теңдеуін

айналу бетінің кезкелген

M x, y, Z нүктесінің координаталары қанағаттандыратын болады. Ал бетте

108

жатпайтын нүктелердің координаталары бұл (6.17) теңдеуін қанағаттандырмайды. Олай болса, (6.17) теңдеуі L сызығының Oz өсін айналудан шыққан айналу бетінің теңдеуі болады екен.

Бұл жерде (6.17) теңдеуінің (6.16) теңдеулерінің екіншісінен оның Y және Z координаталарын

	x	2	y	2
Y				(6.18)

Z z

формулалары арқылы x, y, z координаталарымен ауыстырудан алынғанын көреміз.

Сонымен берілген L сызығының қандайда бір өсті айналуынан шығатын беттің теңдеуін алу үшін мынадай ережеге келеміз:

а) L сызығы Oyz жазықтығында жатса, оның теңдеуі

X 0,

F Y, Z 0

және ол Oz өсін айналатын болса, онда осы айналудан шыққан бет теңдеуі

F 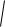x2 y2; z 0; (6.19)

б) L сызығы xOz жазықтығында жатса, оның теңдеуі

Y 0

F X, Z 0

және ол Oz өсін айналатын болса, онда осы айналудан шыққан бет теңдеуі

F x2 y2; z 0; (6.20)

в) L сызығы xOy жазықтығында жатса, оның теңдеуі

Z 0

F X, Y 0

және ол Oy өсін айналатын болса, онда осы айналудан шыққан бет теңдеуі

F		;	y 0;
	x2 z2			(6.21)

г) L сызығы xOy жазықтығында жатса, оның теңдеуі

Z 0

F X, Y 0

болады және ол Ox өсін айналатын болса, онда осы айналудан шыққан беттің теңдеуі

F x;		0
	y2 z2		(6.22)

болады.

Осы төрт жағдайдан олардың барлығына ортақ мынадай ережені қорытып айтуға болады:

L сызығының теңдеулерінің (кеңістіктегі сызық екі беттің қиылысуы ретінде қаралатын болғандықтан) екінші теңдеуінде айналу өсіне сәйкес координатаны өзгеріссіз қалдырып, ал екінші координатаны айналу осінен

109

басқа қалған екі өске сәйкес координаталардың квадраттарының қосындысының квадрат түбіріне ауыстыру керек.

Осы ереже арқылы өзімізге белгілі екінші ретті қисықтардың айналуынан шығатын беттерді жеке-жеке қарастырайық.

6.6 Эллипсоид

xOz жазықтығындағы эллипсті

x2 z2 a2 c2 1

Oz өсінен айналдыратын болсақ, онда шығатын бет эллипсоид деп аталады да, оның теңдеуі ереже бойынша бірден мына

	x2 y2		z2	1	(6.23)
	a2		c2

түрде жазылатын болады (42-сурет).

Енді осы эллипсоидты xOy жазықтығына параллель бір z h h c

жазықтығымен қиятын болсақ, онда оның қимасында теңдеуі

z h
			h2		(6.24)
	x2 y2 a2
		1

c2

болатын шеңбер шығады. Демек, h-тың мәні c-дан c-ға дейін өзгергенде (6.24) шеңбер айналу бет – эллипсоидты созып шығады.

Ал енді (6.24) шеңбердің орнына z h жазықтығында жатқан

z h
		2		y2			h2		(6.25)
x
						1
		2		b	2		c	2
a

эллипсті алатын болсақ, онда ол h-тың мәні c-дан c-ға дейін өзгергенде

эллипсоидты сызып шығады. Оның						теңдеуін			(6.25)-теңдеулерінен h-ты
жойып,
	x2		y2				z2	1	(6.26)
	a2		b2				c2

екенін табамыз.

Бұл теңдеудегі a, b, c эллипсоидтың жарты остері деп аталады. Осы эллипсоидты координаттық z 0, y 0 және x 0 жазықтықтарымен қиятын болсақ, онда оның қимасында сәйкес түрде мына

x

2

y2

1

x

2

z2

1

y2

z

2

1

b2

c2

c2

a

2

;

a2

;

b2

z 0

y 0

x 0

эллипстері шығатын болады.

110

42-сурет	43-сурет
Жалпы a b c деп аталатын болсақ,		онда (6.26) теңдеуімен
анықталатын эллипсоид үш ості эллипсоид деп аталады.
Ал егер a b c болса, онда (6.26) теңдеуімен анықталатын эллипсоид
сфераға айналады.
Егер a b c болса, онда (6.26)	теңдеуі Ox	өсін айналған осы өстің
бойында созылыңқы эллипсоидты анықтайды.
Егер a b c болса, онда (6.26)	айналу өсі	Oz болатын қысылыңқы
эллипсоидты анықтайтын болады.

(6.26) теңдеуінде координаталардың тек квадраттары ғана, демек эллипсоид координаталар жүйесінің бас нүктесіне қарағанда симметриялы болады.

6.7 Бір қуысты гиперболоид

xOz жазықтығындағы

x2 z2 a2 c2 1

гиперболасын Oz өсінен айналдыратын болсақ, онда айналу бетінің теңдеуі

	x2 y2		z2	1
	a2		c2

болады. Бұл теңдеу айналудан шыққан бір қуысты гиперболоид деп аталатын бетті анықтайды (43-сурет).

Бұл гиперболоидты z h жазықтығымен қиятын болсақ, онда оның қимасында

z h
				h2		(6.27)
	x2 y2	a2
			1

c2

теңдеуімен анықталатын шеңбер аламыз. Оның центрі Oz өсінде, ал радиусы

111

r a

1

h2

c2

болады. Демек, h-тың мәні -тен

-ке дейін өзгергенде (6.27) шеңбер

бір қуысты гиперболоидты сызып шығатын болады.

Ал егер (6.27) шеңбер орнына z h жазықтығында жататын

z h

2

y2

h2

(6.28)

x

1

2

b

2

c

2

a

эллипсті алатын болсақ, онда h-тың мәні -тен -ке дейін өзгергенде (6.28) эллипс гиперболоидты сызып шығады. Оның теңдеуін (6.28) теңдеулерінен h-ты шегеріп барып, мына

	x2		y2		z2	1	(6.29)
	a2		b2		c2

түрде болатынын табамыз.

Осы теңдеумен анықталатын екінші ретті бет бір қуысты гиперболоид деп, ал a, b, c оның жарты өстері деп аталады.

Осы (6.29)

теңдеуімен

анықталған

бір

қуысты гиперболоидтың

z 0, y 0 және

x 0

координаттық жазықтықтармен қимасында сәйкес

түрде

x2

y2

1

b2

a2

эллипсін,

z 0

x

2

z2

1

y2

z2

1

және

c2

c2

a

2

b2

y 0

x 0

гиперболаларын алатын боламыз.

Егер a b болса, онда (6.29) теңдеуі айналу өсі Oz болатын бір қуысты гиперболоидты анықтайды.

(6.29) теңдеуінде координаталардың тек квадраттары ғана болғандықтан, гиперболоид координата жүйесінің бас нүктесіне қарағанда симметриялы болады, ал координаттық жазықтықтар оның симметрия жазықтықтары болады.

6.8 Қос қуысты гиперболоид

Қайсыбір координаттық жазықтықта жататын гипербола өзінің нақты өсін айналатын болса, онда одан екі бөлек айналу беттері шығатын болады да, олар қос қуысты гиперболоид деп аталады. Мысалы,

112

z2 x2 1 c2 a2

теңдеуімен анықталатын гиперболаны Oz өсінен айналдыратын болсақ, онда (ереже бойынша) оның теңдеуі

z2 x2 y2 1 c2 a2

болатын қос қуысты гиперболоид шығады (44-сурет). Енді осы

гиперболоидты z h		R		c жазықтығымен қиятын болсақ,						онда оның
қимасында
				x2		y2		z2	1
										(6.30)
						a2		c2

z h

теңдеулерімен анықталатын центрі Oz өсінде жататын, радиусы

h2

r a c2 1

44-сурет 45-сурет

болатын шеңбер шығады. (6.30) теңдеулерде h-тың мәні c-дан -ке дейін өзгеретін болса, онда (6.30) шеңбері гиперболоидтың бір қуысын, ал h-тың мәні c-дан -ке дейін өзгеретін болса, онда (6.30) шеңбер гиперболоидтың екінші қуысын сызып шығатын болады.

Ал егер (6.30) шеңбердің орнына
x2			y2		h2	1
			b2		c2
a2						(6.31)

z h

эллипсін алатын болсақ, онда h-тың мәні -тен c-ға дейін және c-дан-ке дейін өзгергенде (6.31) эллипс қос қуысты гиперболоидты сызып шығатын болады. Ал оның теңдеуін (6.31) эллипс теңдеулерінен параметр h- ты шегеріп тастап, мына

113

	x2		y2		z2	1	(6.32)
	a2		b2		c2

түрде болатынын табамыз.

Сонымен (6.32) теңдеуімен анықталатын екінші ретті бет қос қуысты гиперболоид деп, ал a, b, c оның жарты остері деп аталады.

Ал (6.32) теңдеуімен анықталатын қос

қуысты

гиперболоид

z 0

жазықтығымен қиылыспайды

(6.32)

гиперболоидты

x 0 және

y 0

координаттық жазықтықтармен қиғанда оның қимасында сәйкес

z2

y2

1

z2

x2

1

b2

a2

c2

және

c2

x 0

y 0

теңдеулерімен анықталатын екі гипербола алатын боламыз.

Әрине қос қуысты гиперболоид та координат жүйесінің бас нүктесіне қарағанда симметриялы болады, ал координаттық жазықтықтар оның симметрия жазықтықтары болады.

Егер a b болса, онда (6.32) теңдеуімен анықталған гиперболоид айналу өсі Oz болатын қос қуысты гиперболоидты анықтайды.

Ал егер гипербола басқа жазықтықтарда берілген болса да, нақ осы сияқты қорытындыларға келетін боламыз. Ол дербес жағдайларға тоқталмайақ қоялық.

6.9 Эллипстік параболоид

Қандай да бір координаттық жазықтықта болмасын парабола өзінің симметрия өсін айналатын болса, онда одан шығатын бет айналу параболоиды деп аталады.

Параболоидтың түрін, теңдеуін толық қарастыру үшін, мысалға мына y2 2pz теңдеуімен анықталған параболаны Oz өсінен айналдырайық. Онда оның теңдеуі (ереже бойынша)

	x2 y2		2pz	(6.33)
болады.	Oz			z h h 0
Осы параболоидтың		өсіне перпендикуляр
жазықтығымен қимасында	z h
				(6.34)
	x2 y2		2ph

теңдеулерімен анықталатын, центрі Oz өсінде жататын, ал радиусы r 2ph

болатын шеңбер болады. Демек, h-тың мәні 0-ден -ке дейін өзгеретін болса, онда (6.34) шеңбер айналу параболоидын сызып шығатын болады (45сурет).

Ал енді (6.34) шеңбер орнына z h жазықтығында жататын

114

x2				y2
					1			(6.35)
2ph				2qh
z h,
(мұндағы p, q және h оң сандар)		жарты өстері					және		болатын
						2ph		2qh

эллипсті алайық. h-тың мәні 0-ден -ке дейін өзгеретін болса, онда (6.35) эллипс екінші ретті бетті эллипстік параболоидты сызып шығады. Бұл жағдайдағы оның теңдеуін (6.35) теңдеулерінен h-ты жойып, мына

	x2		y2				x2		y2
				1	немесе					2z	(6.36)
	2pz		2qz				p		q
түрінде табамыз.											x 0 координаттық
Осы эллипстік параболоидтың z 0, y 0 және
жазықтықтармен қималарында сәйкес түрде нүкте және
	x2 2pz				және	y2 2pz
	y 0					x 0

және теңдеулерімен анықталатын екі парабола аламыз.

Осы сияқты қорытындыны басқа координаттық жазықтықта берілген парабола үшін де жасауға болады.

6.10 Гиперболалық параболоид

Гиперболалық параболоидтың ең қарапайым теңдеуі
	x2		y2	2z,	p 0, q 0	(6.37)
	p		q
яғни эллипстік параболоидтың (6.36)					теңдеуінен айнымалы	y2 алдындағы

таңбасы ғана өзгеше.

y 0	жазықтығы xOz (6.37) бетті Oz өсі симметрия өсі болатын
	x2 2pz	(6.38)

парабола бойымен қиятын болады (46-сурет).

46-сурет

Ал x h жазықтығы ( yOz жазықтығына параллель) бұл бетті теңдеулері

115