Г.Н. НИГМЕТОВА КОМПЛЕКСТІК АНАЛИЗ

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ Ш.ЕСЕНОВ АТЫНДАҒЫ КАСПИЙ МЕМЛЕКЕТТІК ТЕХНОЛОГИЯЛАР ЖӘНЕ

ИНЖИНИРИНГ УНИВЕРСИТЕТІ ЖОҒАРЫ МАТЕМАТИКА КАФЕДРАСЫ

Г.Н. НИГМЕТОВА

КОМПЛЕКСТІК АНАЛИЗ

Оқу құралы

Ақтау -2012

ӘОЖ 517(075.8)

ББК 22.16я73

Пікір берушілер: Абай атындағы Қазақ ұлттық педагогикалық университеті профессоры, ф.- м.ғ.д. С.Т. Мұхамбетжанов Ш.Есенов атындағы Каспий мемлекеттік технологиялар және инжиниринг университеті профессоры, ф-м.ғ.к. М.Ш. Тілепиев

Алматы энергетика және байланыс институтының доценті, ф-м.ғ.к. М.Ж. Байсалова

Нигметова Г.Н.

Н55 Комплекстік анализ: Оқу құралы / Г.Н. Нигметова - Ақтау, Ш.Есенов атындағы КМТжИУ, 2012. - 83б.

ISBN 978-601-7349-19-6

Бұл оқу құралы Ш. Есенов атындағы Каспий мемлекеттік технологиялар және инжиниринг университетінде оқитын математика мамандығының «Комплекстік анализ» пәнінің бағдарламасына сәйкес жасалған.

ӘОЖ 517(075.8)

ББК 22.16я73

Ш. Есенов атындағы Каспий мемлекеттік технологиялар және инжиниринг университетінің Оқу-әдістемелік Кеңесінің шешімімен баспаға ұсынылды

ISBN 978-601-7349-19-6

© «Ш. Есенов атындағы КМТжИУ университеті» 2012 ж.

2

Кіріспе

Халыққа білім беру саласындағы жаңа концепция бойынша, жаңа оқу орындарының сатылы (бакалавар, магистр) оқу жүйесіне арналған жаңа бағдарлама құрылғаны белгілі. Сондықтан да, оған сәйкестендіріліп жазылған мемлеметтік тілдегі оқулықтар мен оқу құралдарының қажеттілігі мен тапшылығы кӛптеген қиындықтар туғызуда. Мұндай жағдай, әсіресе, сырттай оқитын студенттерге де қиын болып тұр. Соның ішінде «Комплекстік анализ» пәні бойынша физика-математика мамандықтарына арналған қазақ тілінде оқулықтар мен оқу құралдарының жетіспей жатқандығы белгілі. Ұсынылып отырған оқу құралы физика-математика факультеттерінің барлық мамандықтарының студенттеріне арналған.

«Комплекстік анализ» оқулығы «Комплекстік анализ» пәнінің бағдарламасына сәйкес кредиттік жүйеге лайықты етіп жазылған.

Оқулықта комплекс айнымалы функциялар, оларды дифференциалдау және интегралдау, Лоран қатары, қалындылыр теориясы және оларды интегралдарды есептеуге қолдану тақырыптары бойынша теориялық материалдар, сонымен қатар оларды толықтырып, таңдап алынған үлгімысалдар шешімдерімен берілген. Мұнда берілген тұжырымдардың дәлелдемелері толық қамтылған, барлық қажет жағдайларда графикалық кескіндері келтірілген.

3

I ТАРАУ. КОМПЛЕКС САНДАР

1.1. Комплекс сан туралы ҧғым

Математиканың тарихи даму барысында әр қырынан қойылып, түрліше шешім тауып отырған ең басты мәселелердің бірісан ұғымын дамыту болды. Сан үғымын кеңейту мәселесі алгебра ғылымының ӛз алдына бӛлініп дербес даму жолына түсуін күрт жеделдетті, шешуі болатын теңдеулер класын кӛбейтті, қолданыстағы сандар теориясын байытуды, кеңейтуді талап етті.

Сан ұғымының натурал сандардан нақты сандарға дейін кеңею үрдісі тәжірибенің талаптарымен, сондай-ақ математиканың ӛз мұқтаждықтарымен байланысты болды. Алдымен заттарды санау үшін натурал сандар пайдаланылады. Содан кейін бӛлуді орындаудың қажеттігі оң бӛлшек сандар ұғымына әкеледі; әрі қарай, азайтуды орындау қажеттігі нӛл мен теріс сандар ұғымдарына әкелді; ақырында оң сандардан түбір табу қажеттігі иррационал сандар ұғымына әкелді. Аталған амалдардың бәрі нақты сандар жиынында орындалады. Алайда, бұл жиында орындалмайтын операциялар да қалды, мысалы, теріс саннан квадраттық түбір табу амалы. Олай болса, сан ұғымының одан әрі кеңеюінің, нақты сандардан ерекше, жаңа сандардың пайда болуының қажеттігі бар.

Геометриялық тұрғыдан нақты сандар координаталық түзудің нүктелерімен кескінделеді. Әрбір нақты санға түзудің бір нүктесі сәйкес, ал түзудің әрбір нүктесіне бір нақты сан сәйкес келеді. Координаталық түзу түгелдей нақты сандардың бейнесімен толтырылған, яғни басқаша айтқанда «онда басқа сандарға орын жоқ». Жаңа сандардың геометриялық бейнелерін енді түзу бойында емес, координаталық жазықтықта іздеу керек деген ұйғарым туады. Бірақ координаталық ХОУ жазықтығының әрбір М нүктесін осы нүктенің координаталарымен анықтауға болады. Сондықтан жаңа комплекс сандар деген атпен жаңа ұғым енгізілді. 1545 жылы италиян оқымыстысы Дж. Кардано

x y 10,xy 40

теңдеулер жүйесінің нақты сандар жиынында шешімі жоқ, ал оның шешімін

x

1 / 2

y

1 / 2

5 15,

5 15

түрінде табады. Кардано оларды «таза теріс» немесе «софистикалық теріс» шамалар деп атаған. Бірақ ол мұндай шешуді пайдасыз деп тауып, оларды қолданбауға тырысады.

Комплекс сандардың қасиетін дұрыс бағалаған ең бірінші математик Рафаэль Бомбелли (1526-1573) болды. Ол комплекс сандарды кубтық теңдеуді шешудің «келтірілмейтін» жағдайын шешуге қолданады. Ол 1572 жылы жарық кӛрген «Алгебра» атты еңбегінің бірінші кітабында комплекс сандарға амалдар қолданудың алғашқы ережелерін кӛрсетті. Бомбелли Карданоның

4

«софистикалық теріс сандар» кездесетін барлық ӛрнектердің a bi түріне келетінін тағайындады. 1637 жылы француз математигі Р. Декарт «жорымал сан» терминін енгізді, ал XVIII ғасырдың ең атақты математиктердің бірі Л. Эйлер 1977 жылы 1 (жорымал бірлік) санын белгілеу үшін француз сӛзінің imaginaire (жорымал) бірінші әрпін қолдануды ұсынды. 1831 жылы К. Гаусс «комплекс сан» терминин енгізді.

Жалпы комплекс сандарын интегралдық есептеуде, механикада, геометрияда қолданымдарына байланысты қалыптаса бастаған комплекс айнымалы функциялар теорясының дамуына француз математигі Даламбер, негізі швециялық болса да, ӛзін «орыс ғалымы» деп атап ӛткен Л.Эйлер кӛптеген үлестерін қосқан. Теорияның одан әрі дамуына неміс ғалымдары К.Гаусс, Б.Риман, француз ғалымы О.Кошилердің аттарымен қатар орыс ғалымдары Н.Е.Жуковский, М.А.Лаврентьев, М.В.Келдыштің де еңбектері зор.

1.2. Комплекс сандар және олардың геометриялық кескіні

Комплекс сан z деп белгілі бір тәртіппен алынған х және у қос нақты сандар айтылады және ол алгебралық түрде z=x+iy деп белгіленеді, мұндағы x және y-нақты сандар, ал i- жорымал бірлік деп аталады, i2 1. Комплекс сандар жиыны С әрпімен белгіленеді:

Сz (x, y) : x, y R .

хсаны z комплекс санының нақты бӛлігі деп аталып, х=Re z (Reelle деген француз сӛзінен алынған) арқылы белгіленеді, ал y саны z комплекс санының жорымал бөлігі деп аталып, y=Im z (Imaginaire деген француз сӛзінен алынған) арқылы белгіленеді.

Егер z1 x1 iy1 және z2 x2 iy2 екі комплекс сандарының сәйкес нақты

және жорымал бӛліктері ӛзара тең болса, яғни x1 x2 , y1 y2 , онда олар тең комплекс сандар деп аталады. Дербес жағдайда, z=x+iy комплекс саны нӛлге тең болады, тек сонда ғана, егер x = y = 0 болғанда. Комплекс сандар үшін «артық» және «кем» ұғымдары енгізілмейді.

Бірінші компоненттері ӛзара тең, ал екінші компоненттерінің таңбасы ғана қарама-қарсы екі комплекс сан түйіндес комплекс сандар деп аталып мына түрде белгіленеді:

z x y i және z x y i .

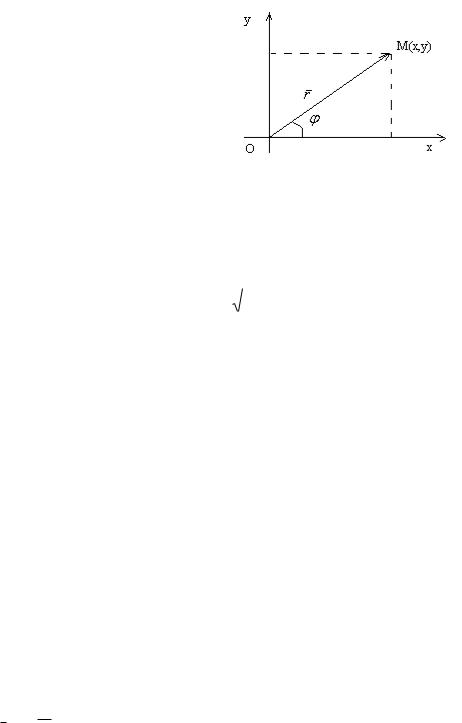
Кез келген z= x+iy комплекс санын Оxy жазықтығында М(x;y) нүктесімен кескіндеуге болады (1-сурет ).

Сонда z C санын М нүктесінің аффиксі деп, а жазықтық комплекс жазықтық (кейде Гаусс жазықтығы) деп аталады. Комплекс сандарды осылайша кескіндегенде нақты сандар абсциссалар осінің нүктелерімен кескінделеді де, ал ординаталар осінің нүктелері таза жорымал сандарды кескіндейді.

Сондықтан абсцисса осін нақты ось деп, ал ордината осін жорымал ось деп атайды.

5

1-сурет

z=x+iy комплекс санын

радиус-векторының кӛмегімен

r OM (x;y)

беруге болады.

векторының ұзындығын z

комплекс санының модулі деп

r

атайды және ол

z

немесе r арқылы белгіленеді:

r =

z

=

x2 y2 .

(1.1)

Демек, -

Ох осін

векторының бағытымен беттестіру үшін оң бағытқа

r

бұратын бұрышты кескіндейді, егер бұру сағат тіліне қарсы бағытта іске асырылса, онда бұл бұрыш оң, қарсы жағдайда – теріс деп есептелінеді.

z=0 комплекс саны үшін аргумент анықталмайды. Әрбір z 0 комплекс саны үшін оның аргументінің біріненбірінің айырмашылығы 2 болатын кӛп мәндері болады. Сондықтан

Argz arg z 2 k ,

мұндағы arg z - аргументтің бас мәні және ол arg z .
Ескерту. Кӛп жағдайда есеп шығару барысында аргументтің бас мәні
		y								x 0;
	arctg		,						егер
		x
				y
arg z	arctg						,		егер	x 0, y 0;
				x							(1.2)
						y
	- arctg							,	егер	x 0, y 0
						x

формуласымен анықталады.

Комплекс санның r модулі мен аргументін комплекс санды кескіндейтін r OM векторының полярлық координатасы ретінде қарауға болады (1-сурет). Сонда x r cos , y= r sin . Демек, z = x+iy комплекс санын

z = r cos +ir sin немесе z= r( cos +i sin )

түрінде жазуға болады. Комплекс санның мұндай жазылуын комплекс санның

тригонометриялық түрі деп атайды.

ei cos i sin

(1.3)

Эйлер формуласын қолдану арқылы z r(cos i sin ) комплекс санын z rei

түрінде жазуға болады. Комплекс санның мұндай жазылуын комплекс санның

көрсеткіштік түрі деп атайды.

6

Мысалы 1.1. z1=-1+i және z2=-1 комплекс сандарын тригонометриялық және кӛрсеткіштік түрде жазыңыздар.

Шешуі. z1 үшін

								1						3
			2	2
z	r	( 1)		1		2	, arg z arctg								,
								1
												4		4

яғни	3		.	Сондықтан
	4
									3			3				i	3
		1 i								i sin				2e
						2 cos											4 .
									4			4
z2 үшін
r		1 2		02	1 , arg z arg( 1) ,												яғни .
Сондықтан 1 cos i sin ei .
				1.3. Комплекс сандарға амалдар қолдану
1. Комплекс сандарды қосу.
z1=x1+iy1 және z2=x2+iy2											екі комплекс санының қосындысы деп
								z1 z2			(x1 x2 ) i( y1 y2 )								(1.4)

теңдігімен анықталатын комплекс санды айтады. Комплекс сандарды қосудың келесі қасиеттері бар:

1.Коммутативтік: z1 z2 z2 z1 ,

2.Ассоциативтік: z1 (z2 z3 ) (z1 z2 ) z3 .

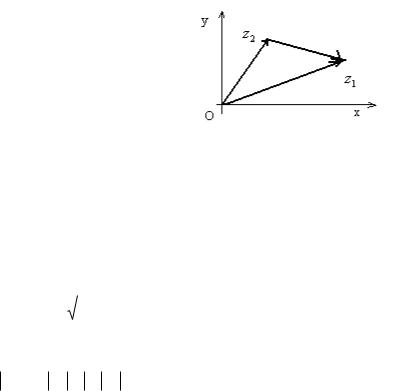
2-сурет

z1 және z2 комплекс сандарының қосындысына геометриялық талдау жасау үшін ол сандарды сәйкес векторлар түрінде кӛрсетеміз. Сонда z1 z2 кескінін екі вектордың қосындысын табудың параллелограмм ережесі бойынша да анықтауға болады (2-сурет).

Екі комплекс санның қосындысының модулі қосылғыштар модульдерінің қосындысынан кем, не тең болатынын 2-суреттен кӛреміз, ӛйткені үшбұрыштың кез келген қабырғасы қалған екі қабырғасының қосындысынан кем:

z1 z2 z1 z2

7

Мысалы 1.2. Амалдарды орындаңыздар: 2 5 i 4 2 i .

Шешуі. 2 5 i 4 2 i 2 4 i 5 2 6 3 i .

2. Комплекс сандарды азайту.

Комплекс сандарды азайту қосуға кері амал ретінде анықталады. z1 x1 y1i және z2 x2 y2i комплекс сандарының айырмасы деп

z2 z z1 немесе (x2	y2i) (x yі) x1 y1і	(1.5)
теңдігін қанағаттандыратын z x yі	комплекс санын атайды.
Бұл анықтамадан z-ті оңай табуға болады:
z1 z2 (x1 x2 ) i( y1	y2 ) .	(1.6)

3-сурет

Айырма үшін z1 z2 z1 ( z2 ) анықтамасын немесе үшбұрыш ережесін қолдануға болады. Осыдан екі санның айырмасының модулінің геометриялық мағынасын алуға болады (3-сурет).

Демек,			z1 z2 айырымының модулі және нүктелерінің ара қашықтығына
тең:
	z1 z2			x1 x2 2 y1 y2 2	d ,

ал екі комплекс санның айырымының модулі олардың модульдерінің айырмасынан артық, не тең:

z1 z2 z1 z2 .

екенін атап ӛтейік, яғни екі комплекс санның айырмасы жазықтықта осы сандармен кескінделетін нүктелердің ара қашықтығына тең.

Мысалы 1.3. Амалдарды орындаңыздар: 10 7 i 6 5 i .

Шешуі. 10 7 i 6 5 i 10 6 i 7 5 4 2 i .

3. Комплекс сандарды көбейту.
z1 x1 y1i	және z2 x2 y2i екі комплекс санның көбейтіндісі деп
	z z1z2 (x1x2 y1 y2 ) i(x1 y2 y1x2 )	(1.7)

теңдігімен анықталатын комплекс санды айтады. Комплекс сандарды кӛбейтудің келесі қасиеттері бар:

1.Коммутативтік: z1 z2 z2 z1 ,

2.Ассоциативтік: z1 (z2 z3 ) (z1 z2 ) z3 ,

3.Дистрибутивтік: z1 (z2 z3 ) z1 z2 z1 z3 .

Мысалы 1.4. Амалдарды орындаңыздар: 2 3 i 5 4 i .

8

Шешуі. (2 3i) ( 5 4i) 10 8 i 15i 12 i 2 10 23 i 12 2 23 i .
Тригонометриялық түрде	берілген	z1 r1(cos 1 i sin 1)	және

z2 r2 (cos 2 i sin 2 ) комплекс сандарының кӛбейтіндісі мына формула арқылы анықталады:

z1z2 r1r2 (cos( 1

2 ) i sin( 1 2 )) .

(1.8)

Бұдан мынадай қорытынды шығады:

z1 z2

z1

z2

,

arg z1 z2 arg z1 arg z2 ,

(1.9)

Комплекс

сандарды

кескіндеу үшін векторларды

пайдалана отырып,

z1 z2 кӛбейтіндісінің векторы

z1 векторынан соңғыны

a r gz2 бұрышына

бұру және k

z2

есе созу арқылы алынады деп айтуға болады.

Дербес жағдайда , егер бірдей п кӛбейткіші бар болса,

zn (r(cos i sin ))n rn (cos n i sin n ) .

(1.10)

Бұдан

z n

z

n ,

arg z n n arg z .

(1.11)

(1.10) формуласын Муавр формуласы деп атайды.

4. Комплекс сандарды бөлу.

Комплекс сандарды бӛлу кӛбейтуге кері амал ретінде анықталады.

z1 x1 y1i		және z2 x2 y2i 0 екі комплекс санның бөліндісі деп
		z2 z z1	(1.12)
теңдігін қанағаттандыратын z x yi санын атайды.
Олай болса
x2 i y2 x i y x1 i y1
теңдігінен
xx2	yy2	x1 ,
	yx2	y1
xy2

жүйесі шығады. Бұл жүйенің бір шешімі бар:

x

x1 x2 y1 y2

,

y

y1 x2 x1 y2

.

x22 y22

x22 y22

Сонымен,

z

z1

x1x2

y1 y2

i

y1x2

x1 y2

.

(1.13)

x2

x2

z

2

y2

y2

2

2

2

2

Мысалы 1.5. Амалдарды орындаңыздар:

1 3i

.

1 3 i 2 i

2 i

1 3 i

2 i 6i 3

5 5i

Шешуі.

2 i 2 i

1

i .

2 i

4 1

5

Тригонометриялық

түрде

берілген

z1 r1(cos 1 i sin 1)

және

z2 r2 (cos 2 i sin 2 )

комплекс сандарының бӛліндісі мына формула арқылы

анықталады:

z

z1

r1 (cos 1 i sin 1 )

r1

(cos( 1

2 ) i sin( 1 2 ))

(1.14)

z2

r 2 (cos 2

i sin 2 )

r2

9

Бұл жағдайда модуль мен аргументтің мынадай қасиетін аламыз:

z

z1

z

1

,

arg

1

arg z

arg z

2 .

(1.15)

z2

z2

1

z2

5. Комплекс саннан түбір табу.

Түбір табу дәрежелеуге кері амал.

z комплекс

санының п

–ші

дәрежелі түбірі

деп

n z теңдігін

қанағаттандыратын комплекс санын айтады,

яғни n z , егер n z .

Егер z r(cos i sin ) ,

ал

(cos i sin )

десек,

онда түбірдің

анықтамасы және Муавр формуласы бойынша

z n n (cos n i sin n ) r(cos i sin )

аламыз. Бұдан

n r, n 2 k, k 0, 1, 2,... ,

яғни

2 k

және n r

(1.16)

n

Сондықтан n z теңдігі мына түрге келтіріледі:

2 k

2 k

Wk n r(cos i sin )

n

i sin

,

k 1, n 1.

(1.17)

r cos

n

n

(1.17) – комплекс саннан түбір табу формуласы.

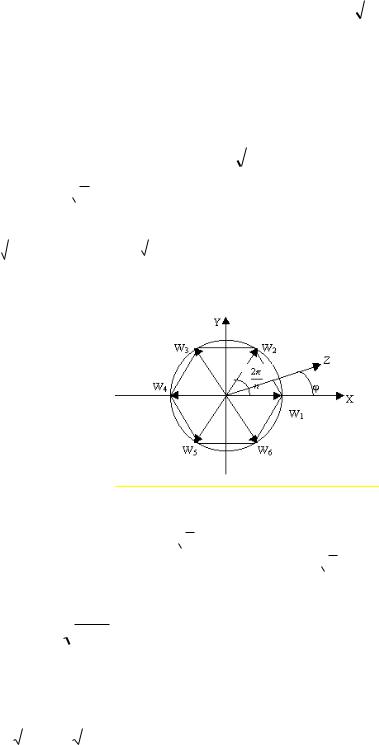
4 –сурет

Геометриялық тұрғыдан nz ӛрнегіндегі бұл n мәнді центрі координата жүйесінің бас нүктесінде және радиусы nr болатын шеңберге іштей сызылған дұрыс n- бұрыштың тӛбелері түрінде кескінделеді (4 –сурет, n=6).

Мысал 1.6. 3 64 мәнін табыңыздар.

Шешуі. Түбір астындағы ӛрнекті тригонометриялық түрде жазамыз:

64 64(cos i sin ) . (1.17) формуласы бойынша

								2 k		2 k		k 0,1, 2 .
k		3	64		3				i sin
						64 cos		3		3	,
										10