- •Змістовий модуль 1
- •Не 1.1. Структура системного програмного забезпечення Структура спз.
- •Місце ос в спз.
- •Поняття операційного середовища.
- •Операційні системи.
- •Системи керування файлами.
- •Інтерфейсні оболонки для взаємодії користувача з ос і програмні середовища.
- •Системи програмування.
- •Утиліти.
- •Основні функції ос.
- •Не 1.1. Базові поняття сучасних операційних систем Базові поняття операційної системи Linux. Файли, каталоги, робота з файлами. Права доступу до файлів і каталогів.Інструментарій.
- •Програми-фільтри. (немає) Командний інтерпретатор.
- •Змістовий модуль 2
- •Не 2.1. Загальна схема роботи компіляторів Визначення транслятора, компілятора, інтерпретатора.
- •Компілятор.
- •Різниця між інтерпретаторами і трансляторами.
- •Етапи трансляції.
- •Поняття проходу. Багатопрохідні і однопрохідні компілятори.
- •Не 2.2. Таблиці ідентифікаторів. Призначення та особливості побудови таблиць ідентифікаторів.
- •Найпростіші методики побудови таблиць ідентифікаторів.
- •Побудова таблиць ідентифікаторів методом бінарного дерева.
- •Не 2.3 Хеш-функції та хеш–адресація. Принципи роботи хеш-функцій.
- •Побудова таблиць ідентифікаторів на основі хеш-функцій.
- •Побудова таблиць ідентифікаторів методом ланцюжка.
- •Комбіновані способи побудови таблиць ідентифікаторів.
- •Змістовий модуль 3. Не 3.1.Кінцеві автомати. Визначення.
- •Детерміновані і недетерміновані кінцеві автомати.
- •Модель ка.
- •Розпізнавачі і перетворювачі. Визначення. Загальні поняття.
- •Класифікація розпізнавачів.
- •Не 3.2.Формальні мови та граматики. Способи завдання мов.
- •Операції над ланцюжками символів.(немає) Поняття мови.
- •Визначення формальної мови.
- •Визначення грамматики.
- •Класифікація граматик.
- •Способи задання схем грамтик Символічна, форма Наура-Бекуса, ітераційна форма й синтаксичні діаграми.
- •Чотири типи граматик по Хомському.
- •Правила побудови граматики із ланцюжка символів. (немає)
- •Змістовий модуль 4.
- •Не 4.1 Лексичні аналізатори (сканери).
- •Принципи побудови сканерів.
- •Призначення лексичного аналізатору.
- •Принципи побудови лексичних аналізаторів.
- •Граф кінцевого детермінованого автомата, що розпізнає граматику цілих чисел мови Сі(Немає) не 4.2.Синтаксичний та семантичний аналіз. Синтаксично-керований переклад.
- •Основні принципи роботи синтаксичних аналізаторів.
- •Дерево розбору. Перетворення дерева розбору в дерево операцій.
- •Призначення семантичного аналізу.
- •Етапи семантичного аналізу.
- •Ідентифікація лексичних одиниць мов програмування.
- •Розподіл пам’яті.
- •Не 4.3. Способи внутрішнього представлення програм Зв'язані облікові структури, що представляють синтаксичні дерева.
- •Багатоадресний код з явно іменованим результатом (тетради).
- •Багатоадресний код з неявно іменованим результатом (тріади).
- •Обернений (постфиксна) польський запис операцій.
- •Алгоритм Дейкстри.
- •Асемблерний код або машинні команди.
- •Розбір арифметичного виразу. Алгоритм Рутисхаузера.
- •Не 4.4 Генерація коду. Методи генерації коду.
- •Загальні принципи генерації коду.
- •Синтаксично керований переклад.
- •Змістовий модуль 5
- •Не 5.1. Керування процесами та ресурсами. Поняття обчислювального процесу та ресурсу.
- •Класифікація ресурсів.
- •Загальна схема виділення ресурсу.
- •Однопрограмний і мультипрограмний режими.
- •Основні риси мультипрограмного режиму.
- •Обчислювальні процеси.
- •Діаграма станів процесу.
- •Реалізація поняття послідовного процессу в ос.
- •Процеси і треди. (немає) Блок керування процесом.
- •Процеси в ос unix.
- •Події (переривання) - рушійна сила, що змінює стан процесів.
- •Механізм обробки переривань.
- •Функції механізму переривань.
- •Групи переривань.
- •Розподіл переривань по рівнях пріоритету.
- •Дисципліни обслуговування переривань.
- •Обробка переривань за участю супервізорів ос.
- •Не 5.2. Планування процесів та диспетчеризація задач. Функції ос, пов’язані з керуванням задач.
- •Організація черг процесів та ресурсів.
- •Priority queuing - (pq)
- •Стратегії планування.
- •Якість диспетчеризації та гарантії обслуговування.(Немає)
- •Безпріоритетні до: лінійні та циклічні.
- •Пріоритетні до: до з фіксованим пріоритетом та до з абсолютним пріоритетом.
- •Адаптивні до. (Немає) Визначення середнього часу знаходження заявки в системі. (Немає) Недоліки до з фіксованим пріоритетом.
- •Динамічне планування (диспетчеризація). (Немає) Диспетчеризація задач з використанням динамічних пріоритетів. Переваги і недоліки.
- •Критерії ефективності обчислювального процесу. (Немає) Методи підвищення продуктивності системи для багатопроцесорних систем.
- •Механізм динамічних пріоритетів в ос unix.
- •Змістовий модуль 6
- •Не 6.4. Керування пам’яттю. Пам'ять і відображення, віртуальний адресний простір.
- •Простий безперервний розподіл і розподіл з перекриттям (оверлейні структури).
- •Розподіл статичними і динамічними розділами.
- •Розділи з фіксованими границями. Розділи з рухливими границями.
- •Виділення пам'яті під новий розділ: перша придатна ділянка; сама придатна ділянка; сама невідповідна ділянка.
- •Сегментна, сторінкова і сегментно-сторінкова організація пам'яті. Сегментний спосіб організації віртуальної пам'яті.
- •Дисципліни заміщення: fifo; lru (1еаst recently used,); lfu (1еаst frequently used); random.
- •Сторінковий спосіб організації віртуальної пам'яті.
- •Сегментно-сторінковий спосіб організації віртуальної пам'яті.
- •Змістовий модуль 7
- •Не 7.1. Ос однопроцесорних кс. Класифікація ос.
- •Режими організації обчислювального процесу. (Немає) Основні принципи побудови операційних систем.
- •Принцип модульності.
- •Принцип функціональної вибірковості.
- •Принцип генерування ос.
- •Принцип відкритої і нарощуваний ос.
- •Принцип мобільності.
- •Принцип забезпечення безпеки обчислень.
Детерміновані і недетерміновані кінцеві автомати.
Кінцеві автомати широко використовуються на практиці, наприклад у синтаксичних, лексичних аналізаторах, і тестуванні програмного забезпечення на основі моделей.
Кінцеві автомати поділяються на детерміновані та недетерміновані.
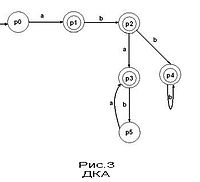
Детермінований кінцевий автомат
Детермінованим кінцевим автоматом (ДКА) називається такий автомат, в якому для кожної послідовності вхідних символів існує лише один стан, до якого автомат може перейти з поточного.
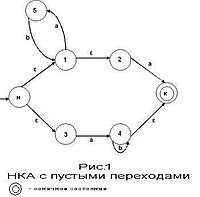
Недетермінірованний кінцевий автомат (НКА) є узагальненням детермінованого. Недетермінірованность автоматів досягається двома способами:
|
Існують переходи, помічені порожній ланцюжком ε |
З одного стану виходить кілька переходів, помічених одним і тим же символом |
|
|
|
Якщо розглянути випадок, коли автомат
заданий наступним чином:
![]() , Де:
, Де:
S - безліч стартових станівавтомата, таке що
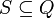 ;
;
Тоді з'являється третя ознака недетермінізма
- наявність декількох початкових
(стартових) станів у автомата
![]() .
.
Існує теорема, яка говорить, що "Будь недетермінірованний кінцевий автомат може бути перетворений в детермінований так, щоб їхні мови збігалися" (такі автомати називаються еквівалентними). Однак, оскільки кількість станів в еквівалентному ДКА в гіршому випадку зростає експоненціально із зростанням кількості станів вихідного НКА, на практиці подібна детермінізації не завжди можлива. Крім того, кінцеві автомати з виходом в загальному випадку не піддаються детермінізації.
В силу останніх двох зауважень, незважаючи на велику складність недетермінованих кінцевих автоматів, для завдань, пов'язаних з обробкою тексту, переважно застосовуються саме НКА.
Модель ка.
Кінцевий автомат- абстрактний автомат без вихідного потоку, число можливих станів якого звичайно. Результат роботи автомата визначається за його кінцевого стану.
Існують різні варіанти завдання кінцевого
автомата. Наприклад, кінцевий автомат
може бути заданий за допомогою п'яти
параметрів:
![]() , Де:
, Де:
Q - множина станівавтомата;
q 0-початкове (стартове) станавтомата (
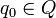 );
);F - множина заключних(абодопускають)станів, таких що
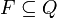 ;
;Σ - допустимий вхідний алфавіт(кінцеве безліч допустимих вхідних символів), з якого формуються рядки, зчитувальні автоматом;
δ - задане відображення множини
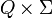 в безліч
в безліч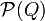 підмножин Q:
підмножин Q:
![]()
(Іноді δ називають функцією переходів автомата).
Автомат починає роботу в стані q 0,зчитуючи по одному символу вхідного рядка. Лічені символ переводить автомат в новий стан з Q відповідно до функції переходів. Якщо після завершення зчитування вхідного слова (ланцюжки символів) автомат виявляється в одному з допускають станів, то слово "приймається" автоматом. У цьому випадку говорять, що воно належить мові даного автомата. В іншому випадку слово "відкидається".
Розпізнавачі і перетворювачі. Визначення. Загальні поняття.
Існує дві різних групи автоматів: Акцептори/Розпізнавачі і Перетворювачі(Трансдуктори).
Акцептори і розпізнавачі
СА акцептор: виконує розбір слова "nice"
Акцептори і розпізнавачі (також виявлювачі послідовностей) продукують двійковий вихід, кажучи або так або ні на питання прийняті автоматом вхідні дані чи ні. Всі стани СА можуть бути або допустими або ні. Коли всі вхідні дані оброблені, якщо поточний стан є допустимим, значить вхід прийнятий; інакше відхилений. Як правило на вхід подаються символи (літери); дії не використовуються. Приклад на зображенні показує СА який приймає слово «nice». В цьому СА єдиний допустимий стан це 7.
Автомат також може бути описаний як такий, що визначає мову, яка містить всі слова розпізнавані цим автоматом, але не ті які ним відхиляються; тоді ми кажемо, що ця мова розпізнається автоматом. За визначенням, мови розпізнавані СА це регулярні мови тобто мова є регулярною якщо існує деякий СА, який розпізнає її.
Початковий стан
Початковий стан зазвичай показується зі стрілкою «звідкись».
Допустимі (або кінцеві) стани
Приклад скінченного автомата; цей приклад показує автомат, який визначає чи двійкове число має непарну кількість 0, де це допустимий стан.
Допустимі стани (також відомі як кінцеві стани) це такі, що якщо автомат знаходиться в них це означає, що вхідний рядок, наскільки він опрацьований, належить мові що розпізнається. Зазвичай позначається двома колами.
Приклад допустимого стану з'являється в діаграмі праворуч: a детермінований скінченний автомат (ДСА), що визначає чи двійковий вхідний рядок містить парну кількість 0.
S1 (який є початковим станом) показує стан в якому парна кількість 0 була введена. Цей автомат опиниться в допустимому стані, якщо двійковий рядок містить парну кількість 0 (включно з рядком, що не містить 0 взагалі). Приклади рядків розпізнаваних цим ДСА це порожній рядок, 1, 11, 11..., 00, 010, 1010, 10110, і подібні ...
Перетворювачі (Трансдуктори)
Перетворювачі виробляють вихід, що базується на даному вході і/або на станах з використанням дій. Вони використовуються для керування і в галузі математичної лінгвістики. Тут вирізняють два типи: