Означення спільного дільника та найбільшого

спільного дільника многочленів. Властивості НСД.

Означ.2. Многочлен називається спільним дільником многочленівта, якщота.

Зауважимо одразу, що спільних дільників двох многочленів є безліч (наприклад, ще всі ненульові константи).

Означ.3. Многочлен називається найбільшим спільним дільником многочленівта, якщо:

а) – є спільним дільникомі;

б) , де– довільний спільний дільник многочленіві.

Позначення:

Властивість 1. – так прийнято вважати.

Властивість 2. .

Властивість 3. Якщо , то

Доведення випливає з означення НСД та властивості подільності многочленів.

Алгоритм Евкліда знаходження нсд двох многочленів .

Як випливає із властивостей НСД двох многочленів, НСД двох многочленів не визначається цілком однозначно (вл. 3):

якщо , то

.

Проте з точністю до сталого числового множника НСД двох многочленів визначається однозначно.

При знаходженні НСД цілих чисел елементарним способом дані числа розкладають на прості множники і утворюють добутки усіх спільних простих множників. Але на даному етапі поширити цей метод на многочлени немає можливості, бо ми ще не знаємо методів розкладу многочленна довільного степеня на множники. Крім того поняття “простого множника” для многочленна ще не з’ясовано. Але для знаходження НСД двох цілих чисел застосовують ще один метод – так званий алгоритм послідовного ділення, або алгоритм Евкліда (Евклід виклав цей метод у геометричній формі у 7-й книзі своїх “Начал”).

Алгоритм Евкліда.

Нехай задано два многочлени та.

(Нагадаємо, що ;).

Виконуємо послідовне ділення:

а) на– позначимо частку,

остачу ;

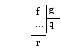
б) Ділимо на остачу– частка,

остача ;

в) Ділимо на остачу– частка,

остача ;

І так далі – послідовно ділимо частку на остачу.

Запишемо це у вигляді рівностей:

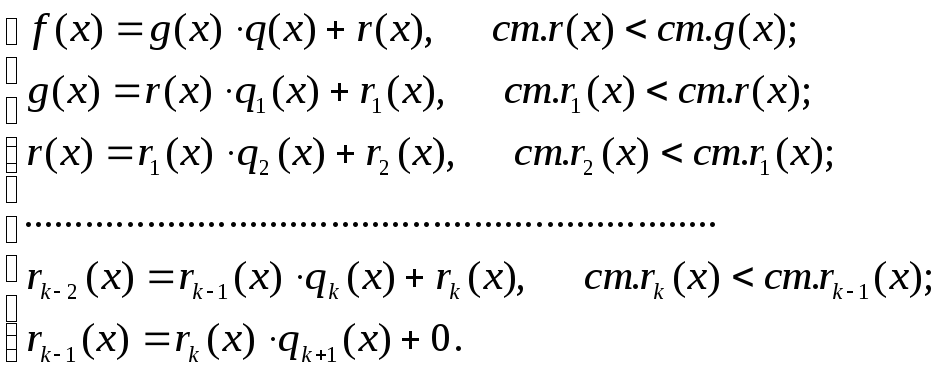(2)

Степені многочленів, які отримаємо в остачі,

будуть утворювати спадну послідовність, але оскільки вони є цілими невід’ємними числами, то така послідовність не може бути безкінечною. Отже, такий процес ділення не може бути нескінченним – нарешті ми прийдемо до остачі , яка є дільником попередньої остачі(тобто).

Доведемо тепер, що ця остання остача і буде.

Для цього розглядаємо рівності (2) і міркування будемо проводити знизу вверх.

Із останньої рівності (2) .

Тоді, враховуючи властивості подільності многочленів, із попередньої (передостанньої) рівності маємо:

і т.д.

;

,

спільний дільник многочленів і. Залишається перевірити, що– це НСД. Нехай– довільний інший спільний дільник многочленівта. Тобтота.

Із першої рівності формул (2)

.

Підставляючи це в другу рівність (2) маємо, що

і т.д.

Це і означає, що .

Формули (2) описують послідовне ділення з остачею, яке називають алгоритмом Евкліда знаходження НСД двох многочленів.

Сформулюємо ще раз доведене вище твердження про НСД двох многочленів:

Теорема 1: НСД двох ненульових многочленів тадорівнює останній ненульовій остачі в алгоритмі Евкліда:

(3)

Доведення. Вище.

Приклад:

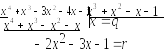
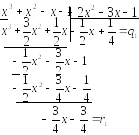
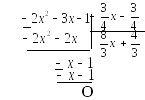
Отже, .

Теорема 2: НСД многочленів тає єдиним з точністю до множника нульового степеня.

Доведення. Нехай два НСД многочленівта. Тоді із означення НСД

та .

Враховуючи властивість 9 подільності многочленів

Що й вимагалося.

Наслідок. Можна домовитися, що старший коефіцієнт НСД двох многочленів будемо вважати завжди рівний одиниці.

Теорема 3: Якщо , то існують такі многочлени,, що

(4)

При цьому, якщо степені многочленівтабільші нуля, то многочленитаможна вибирати так, щоб

(5)

Доведення базується на рівностях (2) алгоритму Евкліда. Оскільки , то покладемо

,

Тоді передостання із рівностей (2) дає:

.

Підставляємо сюди вираження черезтапопередньої з рівностей (2) матимемо

,

де

Продовжуючи піднімання вверх по рівностях (2), отримаємо, нарешті, потрібну рівність (4).

Для доведення другої частини теореми припустимо, що многочлени та, які задовольняють умову (4), вже знайдені, але нехай

Тоді поділимо на:

де

Підставимо останню рівність у (4):

(6)

де

а згідно з припущенням і діленням на.

Покажемо, що .

Припустимо навпаки, що Тоді із останньої рівності (6) маємо, що

()

Оскільки то

()

Крім того, оскільки , то

()

Підставимо ці міркування в ():

де

.

Тобто

Але, згідно з припущенням,

Отже, припущення невірне, тобто Тобто многочлени задовольняє (5). Теорему доведено повністю.

Зауваження: Рівність (4) дає можливість побудувати лінійне вираження НСД многочленів тачерез ці многочлени.

НСД декількох многочленів .

Узагальнимо поняття НСД для декількох многочленів .

Означ. 4. НСД многочленів називається такий їх спільний дільник, який ділиться на довільний інший їх спільний дільник.

Теорема 4:

Доведення. Методом математичної індукції.

Взаємно прості многочлени.

Їх властивості.

Означення взаємно простих многочленів

Властивість 7 із §4.2. твердить, що кожен многочлен ділиться на довільний многочлен нульового степеня:

Тому всі многочлени нульового степеня є спільними дільниками довільних двох многочленів та.

Якщо ж інших спільних дільників ці многочлени не мають, то їх називають взаємно простими.

Означ.1. Многочлени таназиваютьсявзаємно простими, якщо

(1)

Оскільки НСД двох многочленів визначається лише з точністю до множника нульового степеня, то можна вважати, що та–взаємно прості, якщо

(2)

Згідно з теоремою 3 попереднього §4.2., такі, що

(3)

де

для взаємно простимих многочленів.

Властивості взаємно простих многочленів

Властивість 1. Якщо

то

Доведення. Оскільки , то, згідно (3), :

Кожен спільний дільник многочленів та повинен бути дільником і ,але

Властивість 2. Якщо та

то

Доведення. Оскільки

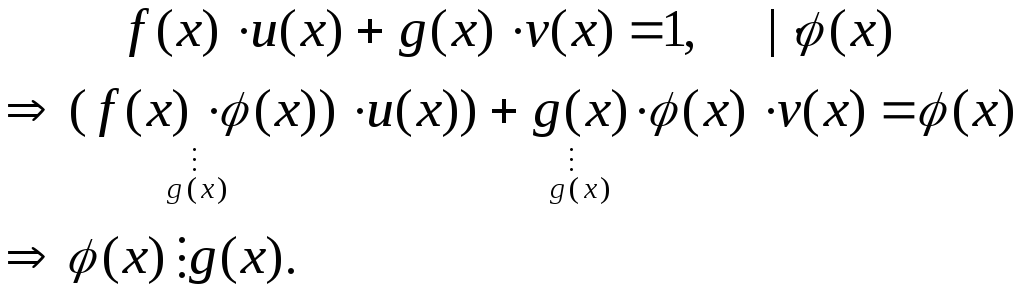
Властивість 3. Якщо та , де

то

Доведення. Оскільки

Крім того

Оскільки , то, згідно з властивістю 2,

Отже,

Із властивістю 2 методом математичної індукції можна отримати наступну

Властивість 4. Якщо многочлен взаємно простимий з кожним з многочленів то вінвзаємно простимий з їх добутком:

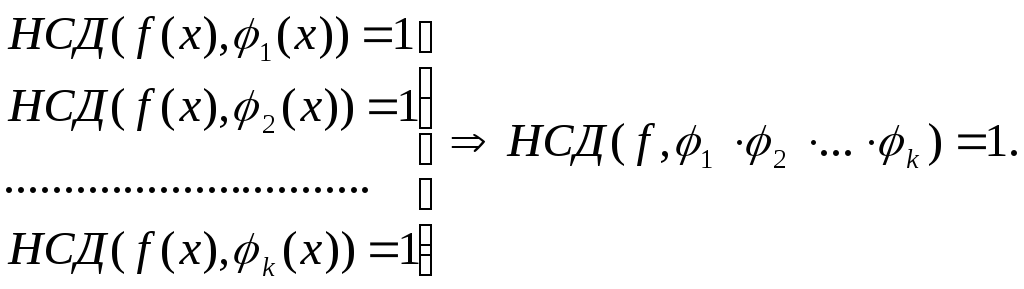
Доведення. Методом математичної індукції із властивістю 1.

Наслідок. Якщо то

Взаємно простота скінченої кількості многочленів

Означ.2. Многочлени називаютьсявзаємно простими, якщо їх

Означ.3. Многочлени називаються попарновзаємно простими, якщо кожні два з них є взаємно простими.

Твердження: Якщо многочлени попарно взаємно прості, то вони всі взаємно прості.

Обернене твердження невірне.

Приклад.

Многочлени взаємно прості, бо

Але вони не попарно взаємно прості, бо