Оценка адекватности нелинейной парной регрессии.

Для оценки адекватности парной нелинейной регрессии наблюдаемым данным можно использовать критерий Фишера. Расчетное значение критерия Фишера находится по формуле:

, (12)

где ,,

n - число опытов, m - число включенных в регрессию факторов.

Для заданного уровня значимости и числа степеней свободы,находится табличное значение. Полученное расчетное значение сравниваем с табличным.

Расчетное значение критерия Фишера также можно определить с помощью индекса корреляции R^'.

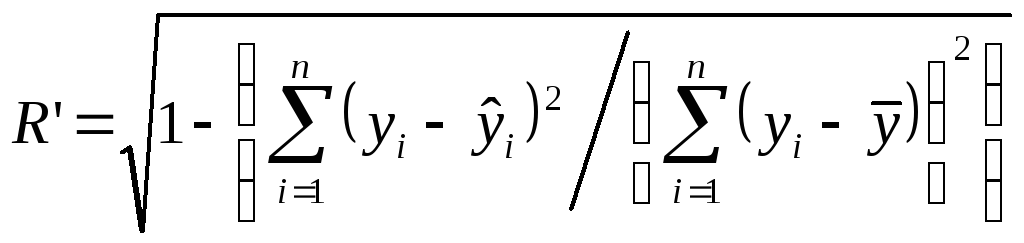, (13)

.

Прогноз и его доверительный интервал для парной нелинейной регрессии.

Точечная оценка прогноза находится по формуле:

, где . (14)

Интервал значимости вычисляется как , где

.

Средние коэффициенты эластичности для линейной регрессии расчитываются по формуле:

Э y_xj = а_j x_j / y

Множественная регрессия.

Для измерения тесноты связи между двумя из рассматриваемых переменных ( без учета их взаимодействия с другими переменными ) применяются парные коэффициенты корреляции:

r _yx1 = ( x₁y –x₁ y ) /σ _x1 σ_y ; r _yx2 = ( x₂y – x₂ y ) /σ _x2 σ_y ;

r _x1x2 = ( x₁ x₂ – x₁ x₂ ) /σ _x1 σ _x2 . (15)

где

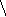
σ _x1 = x₁ ² - ( x₁)²

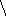
σ _x2 = x₂ ² – (x₂) ²

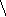
(16)

σ_y = y ² – (y )²

Так как в реальных условиях все переменные, как правило,взаимосвязаны, то на значение коэффициента корреляции частично влияют другие переменные В связи с этим возникает необходимость исследовать частную корреляцию между переменными при исключении ( элиминировании ) влияния одной или нескольких переменных. Теснота этой связи определяется частными коэффициентами корреляции.между переменными Xi и Xj при фиксированных значениях остальных m - 2 переменных по формуле:

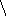
r_{xixj ( x 1,x 2 , …, x m )} = - Аij / A ii * Ajj , (17)

где A ii и Ajj -алгебраические дополнения элементов rii и rjj матрицы парных коэффициентов корреляции ∆ r ₁₁ или по рекуррентной формуле:

r _{xixj ( x 1,x 2,…,x i-1 ,x i+1 , …, x j-1, x j+1, … ,x m )} =

r_{xixj, x 1,x 2,x i-1 ,x i+1 , …, x m -1} - r_{xixm (x 1,x 2, …, x m –1)} r_{xj x m(x 1,x2,…,xm -1)}

( 1 – r²_{xixm( x 1,x 2, …, x m –1)} ) ( 1 – r²_{xj x m(x 1,x2,…,xm -1)} )

Частные коэффициенты ( индексы ) корреляции, измеряющие степень и влияние на у фактора хi при неизменом уровне других факторов, можно определить по рекуррентной формуле :

r _{yxi ( x 1,x 2,x i-1 ,x i+1 , …, x m )} =

r_{yxi,x1,x2,x i-1 ,x i+1 ,…, xm -1} - r_{yxm (x 1,x 2, …, x m –1)} r_{xi x m(x 1,x2,…,xm-1)}

( 1 – r²_{yxm( x 1,x 2, …, x m –1)} ) ( 1 – r²_{xi x m(x 1,x2,…,xm -1)} )

В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: при исключении влияния одной переменной получим частный коэффициент корреляции первого порядка; при исключении влияния двух переменных - частный коэффициент корреляции второго порядка и т. д.

Для двухфакторной модели частный коэффициент корреляции первого порядка между признаками х₁ и у при исключении признака х₂ вычисляют по формуле:

r_{y x 1} - r_{yx 2} r_{x 1x2}

r _{yx1 ( x 2 )} = ___________________________ (18)

( 1 – r²_{yx 2} ) ( 1 – r²_x1x2 )

Для двухфакторной модели частный коэффициент корреляции первого порядка между признаками х₂ и у при исключении признака х₁ вычисляют по формуле:

r_{y x 2} - r_{yx 1} r_{x 1x2}

r _{yx2 ( x 1 )} = ___________________________ (19)

( 1 – r²_{yx 1} ) ( 1 – r²_x1x2 )

Для двухфакторной модели частный коэффициент корреляции первого порядка между признаками х₁ и х₂ при исключении влияния результативного признака у вычисляют по формуле:

r_{х1 x 2} - r_{yx 1} r_уx2

r _{х2x1 ( у )} = _________________________

( 1 – r²_{yx 1} ) ( 1 – r²_уx2 ) ,

где r – парные коэффициенты корреляции между соответствующим признаками.Очевидно, что коэффициент корреляции r между остатками будет отражать тесноту частной корреляции между переменными х_i и х_j при исключении влияния остальных переменных.Можно показать, что коэффициент корреляции r между остатками равен частному коэффициенту корреляции r_xixj.Частный коэффициент корреляции , как и парный коэффициент rij , может принимать значения от –1 до 1 и его значимость оценивают так же, как и обычного коэффициента корреляции r, но при этом полагают n₁ = n – m –2.

Изучение парных и частных коэффициентов корреляции позволяет отобрать наиболее существенные, значимые факторы. Тесноту совместного влияния факторов на результат оценивает коэффициент (индекс )множественной корреляции R yx₁x₂,…,x_m :

R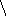 yx₁x₂,…,x_{m =} 1-σ²_{y ост.} /σ²_y

Значение коэффициента (индекса) множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции r _yxi .

Совокупный коэффициент ( индекс ) множественной детерминации опреде

ляет только качество выравнивания по уравнению регрессии. Так как многофакторный регрессионный анализ оперирует случайными наблюдениями, и необязательно распределенными по многомерному нормальному закону ( этому закону должны подчиняться отклонения фактических значений регрессанда от расчетных ), то показатели множественной регрессии и корреляции сами могут оказаться подверженными действию случайных факторов. Поэтому только после проверки адекватности уравнения оно может использоваться для экономического анализа.

Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F– критерия Фишера:

F = R²(n-m-1) / (1- R²). m, или F = σ ²_у .(n-m-1) / σ ²_ост.. m

где m -число факторов.( число параметров р = m + 1 )

Полученное значение F– критерия ( F_расч. ) сравнивают с табличным для принятого уровня значимости и чисел степеней свободы k₁ = m и k₂ = n-m-1.

Если F_расч. > F_табл. , то уравнение регрессии статистически значимо, т.е.

доля вариации, обусловленная регрессией, намного превышает случайную ошибку.

Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если F_расч. > F_табл не менее чем в 4 раза.

Частный F– критерий Фишера оценивает статистическую значимость присутствия каждого из факторов в уравнении регрессии и определяется по формуле:

R² yx₁x₂,…,x_m - r ²_{yxi (x 1,x 2,x i-1 ,x i+1 , …, x m)} .(n-m-1)

F_част. = -------------------------------------------------------------. (20)

R² yx₁x₂,…,x_m

Для оценки значимости коэффициентов регрессии при линейной зависимости используют t - критерий Стьюдента при n –(m + 1 ) степенях свободы :

t_a1 = a₁σ_x1 *√1-r²_x1x2 * √n-m-1 / σ_y √1-R²yx₁x₂

t_a2= a₂σ_x2 * √1-r²_x1x2 * √n-m-1 / σ_y√1-R²yx₁x₂ (21)

t_Ryx1x2 = Ryx₁x₂ * √n-m-1 / √1-R²yx₁x₂

Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.

Оценку значимости коеффициентов регрессии с помощью t – критерия

используют, также, для отбора существенных ( информативных ) факторов при многошаговом регрессионном анализе.Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают

тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем строится уравнение регрессии без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэфициентов регрессии. Процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов.В некоторых случаях расчетное значе ние t _расч. находится вблизи t_табл. , поэтому с точки зрения содержательности модели такой фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов.

На основе коэффициентов регрессии невозможно указать какой из фактор-

ных признаков оказывает наибольшее влияние на результативный признак у, так как они не сопоставимы между собой, поскольку измеряются разными единицами.На их основе невозможно также установить в развитии каких фак

торных признаков заложены наиболее крупные резервы изменения регрессанда у , потому что в них не учтена вариация факторных признаков.

Для ответа на выше перечисленные вопросы построим уравнение множественной регрессии в стандартизированном виде:

t_y = β_ıt_{x ı} + β₂t _{x 2} + … + β_pt_{x p} (22)

где

t_y = у – у /σ_у , t_хi = ( x_i – x_i) /σ_xi - стандартизованные переменные, β_i –

стандартизованные коэффициенты.

Стандартизованные коэффициенты регрессии (β - коэффициенты ) опре-

деляются из следующей системы:

β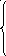₁ + β₂ r_x1x2 + β₃ r_x1x3 + … + β_p r_x1xp = r_yx1

β₁ r_x2x1 + β₂ + β₃ r_x2x3 + … + β_pr_x2xp = r_yx2

…………………………………………………..

β₁ r_xpx1 + β₂ r_xpx2 +β₃ r_xpx3 + … + β_p = r_yxp

и показывают на какую часть среднего квадратичного отклонения изменяется регрессанд у ( результативный признак у ) с изменением соответствующего факторного признака на величину его среднего квадратичного отклонения. С помощью β – коэффициентов определяют факторы в развитии которых заложены наиболее крупные резервы изучаемого показателя.

Так как связь коэффициентов множественной регрессии a_i со стандартными коэффициентами β_i (β – коэффициентами) описывается соотношениями:

a_i = β_iσ_у / σ_xi ; a₀ = y - b₁ x₁ - b₂ x₂ - … - b_p x_p ,

то β - коэффициенты можно также найти по формулам:

β_i = a_i σ_xi / σ_у,

Средние коэффициенты эластичности для линейной регрессии расчитываются по формуле:

Э y_xj = а_j x_j /y

Частные коэффициенты эластичности вычисляются по формуле:

Э y_xj = а_j x_j /ŷ_{xi (x1,x2,xi-1, xi+1,…,xm)}

и показывают на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1% сответствующего фактора при фиксированном положении других факторов.

С помощью частных коэффициентов эластичности можно определить фак-

тор оказывающий наибольшее влияние на регрессанд у ( без учета различия в степени варьирования входящих в уравнение факторов, что, в отличие от β – коэффициентов не дает возможности определить факторы в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя).

Для определения доли вклада анализируемого фактора в суммарное влияние всех факторов вычисляют ∆і - коэффициент по формуле:

∆_і = β_іr_і/R²

С помощью ∆і – коэффициентов можно определиться фактор, развитием которого можно обеспечить наибольшую долю прироста регрессанда у.

Таким образом на основании частных коэффициентов эластичности Э y_xj ,β_i - , ∆і - коэффициентов можно судить о резервах роста исследуемого показателя у (регрессанда у ) которые заложены в том или ином факторе x_i.