95. Как расположены прямая и эллипс? Найти точки пересечения данной прямой и эллипса 10x² +40y² = 400, 2x + y - 7 = 0.

96. Как расположены прямая и гипербола? Найти точки пересечения данной прямой и гиперболы 16x² - 25y² = 400, 7x -5 y = 0.

97. Найти уравнения прямых параллельных и перпендикулярных данной прямой и касающихся данного эллипса. Найти расстояние между парами параллельных касательных x²/30 + y²/24 = 1, 4x - 2y + 23 = 0.

98. Написать уравнение плоскости , проходящей через точку M₀ и нормальный вектор n. Привести его к общему виду и найти расстояние от начала координат до данной прямой. Написать для полученной плоскости  уравнение в отрезках на осях M₀(3,-6,-4), n(-2,5,6).

99. Написать уравнение плоскости , проходящей через точку M₀ и направляющий вектор s₁, s₂. Привести его к общему виду и найти расстояние от точки М₁ до данной плоскости. Написать для полученной плоскости  уравнение в отрезках на осях: M₀(2,6,-2), s₁(2,-2,3), s₂(4,-2,0), М₁(3,-5,0).

100. Написать уравнение плоскости , проходящей через три точки M₁, M₂, M₃. Привести его к общему виду. Найти нормальный и направляющий векторы плоскости . Найти расстояние от начала координат до данной плоскости . M₁(7,0,2), М₂(5,5,2) , М₃(0,1,-5).

101. Написать уравнения плоскостей, делящих пополам двугранные углы, образованные плоскостями  и : : 2x - y+5z - 3 = 0, : 2x- 10y+4z -2 = 0.

102. Написать каноническое уравнение прямой, образованное пересечением двух плоскостей. Найти угол между каждой парой прямых и расстояние между каждой парой прямых

103. Дана прямая L и точка М. Найти: уравнение плоскости, проходящей через прямую L и точку М; уравнение плоскости, проходящей через точку М перпендикулярно прямой L; уравнение перпендикуляра из точки М на прямую L; расстояние от точки М до прямой L; проекцию точки М на прямую L.: М(1,3,-2).

104. Дана прямые L₁, L₂. Установить взаимное расположение прямых. Найти: угол между прямыми; уравнение плоскости, проходящей через прямую L₂ параллельно L₁ ; расстояние между прямыми; уравнение общего перпендикуляра к прямым: .

105. Найти точку M симметричную точке M₀ относительно прямой 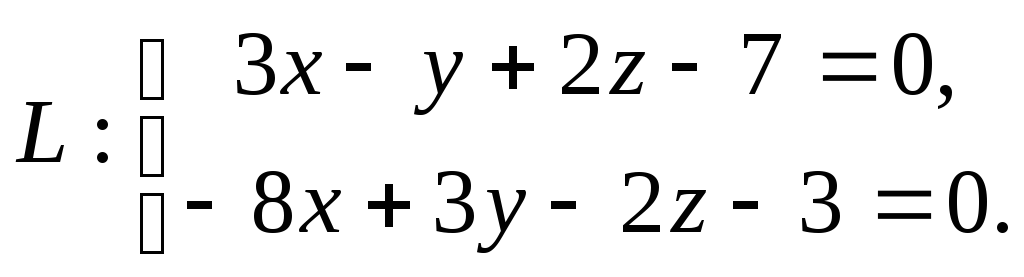М₀(1,0,4).

106. Найти точку M симметричную точке M₀ относительно плоскости : x + y +5 z - 1 = 0, М₀(4,-1,0).

107. Вычислить ранг данных матриц двумя способами: методом элементарных преобразований и методом окаймления миноров .

108. Является ли данная система векторов линейно - зависимой или линейно независимой? a₁ = (1, 0, -1, 0), a₂ = (1, 3, 1, 2), a₃ = (1, 1, 1, -1), a₄ = (-1, 1, -2, 0).

109. При каких  данная система векторов линейно - зависима, и когда она линейно независима? a₁ = (1, 0, -1, 0), a₂ = (1, 3, 1, -1), a₃ = (-1, -1, 2, 1), a₄ = (1, -2, -1, ).

110. Найти базис системы векторов и выразить вектора, не входящие в базис через вектора базиса: a₁ = (1, 2, 3, 0), a₂ = (1, 3, 1, -1), a₃ = (-1, -1, 2, 1), a₄ = (3, 6, 2, -2).

111. Найти базис и размерность подпространства, натянутого на систему векторов: a₁ = (2, 1, 3, -1), a₂ = (-1, 1, -3, 1), a₃ = (4, 5, 3, -1), a₄ = (1, 5,-3, 1).

112. Исследуйте и решите систему линейных уравнений. Найдите общее и одно частное решение СЛУ .

113. Исследуйте и решите систему линейных уравнений в зависимости от параметра ..

114. Найдите фундаментальную систему решений однородной системы линейных уравнений: .

115. Пусть a = (₁, ₂), b = (₁, ₂) любые векторы из R² .Какие из формул в векторном пространстве R² определяют скалярное произведение? Какие из этих пространств евклидовы? 1) a b = ₁₁+ k₂₂ (k R, k  0); 2) a b = ₁₁+ ₂₂+ k (k R, k  0).

116. Ортогонализируйте системы векторов.a₁ = (1, 1, -1, 2), a₂ = (1, 0, 1, 1), a₃ = (0, 1, 3, -1), a₄ = (-1, 2, -2, 0).

117. Вычислите матрицу Грама. Постройте ортонормированный базис подпространства натянутого на данную систему векторов V = L(b₁, b₂, b₃), b₁=(2, 2, 3), b₂=(1, 1, 3), b₃=(2, 3, 2).

118. Найдите ортонормированный базис ортогонального дополнения подпространства, натянутого на систему векторов L = L(b₁, b₂, b₃), b₁=(1, 2, -1, 3), b₂=(1, 1, -1, 0), b₃ =(-1, 1, 1,1);

119. Найдите ортонормированный базис подпространства решений системы однородных линейных уравнений и базис его ортогонального дополнения;.

120. Пусть x = (x₁, x₂, x₃). Является ли преобразование A: R³  R³ линейным оператором? Ax = (x₁+ x₂, x₁+x₃-x₂, x₁) . Если A - линейный оператор, то найти матрицу этого линейного оператора относительно базиса e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1) . Найти ядро, образ, ранг и дефект этого линейного оператора.

121. В пространстве R³ найти матрицу перехода от базиса v₁=(1,0,1), v₂=(1,3,0) , v₃=(0,1,1) к базису u₁=(2,3,-2), u₂=(1,-1,0), u₃=(2,-1,1) и обратно.

122. Пусть x = (x₁, x₂, x₃). Найти матрицу линейного оператора B: R³  R³ относительно базиса v₁=(1,1,0), v₂=(0,1,1), v₃=(1,1,1): Bx = (x₁- x₂, x₁+x₃, x₁) .

123. Пусть x = (x₁, x₂, x₃). В R³ найти собственные векторы и собственные значения линейного оператора A. Ax = (x₁+ x₂, x₁+x₃-x₂, x₁) .

124. Найти собственные векторы и собственные значения линейного оператора, имеющего данную матрицу и действующего в пространстве R³

125. Найти собственные векторы и собственные значения линейного оператора, имеющего данную матрицу и действующего в пространстве R² ,

126. Найдите сопряженный оператор A* для оператора A поворота пространства V₂ векторов плоскости на угол . Вычислить матрицу оператора A*.

127. Найдите сопряженный оператор A* для оператора A подобия пространства V₂. Вычислить матрицу оператора A*.

128. В линейной оболочке L = L(sin x, cos x) скалярное произведение элементов f₁ = A₁sin x + B₁cos x, f₂= A₁sin x + B₁cos x введено по формуле. (f₁, f₂) = A₁A₂ + B₁B₂ + (1/2)(A₁B₂ + B₁A₂). Найти ортонормированный базис пространства . Найти матрицу оператора и сопряженного. Является ли оператор самосопряженным.

129. Найти собственные векторы и собственные значения линейного оператора, действующего в евклидовом пространстве и имеющего в ортонормированном базисе e₁, e₂, e₃ матрицу. Составить матрицу из собственных значений

130. Найти матрицу сопряженного оператора A* в базисе f₁= e₁+ e₂+ e₃, f₂=e₂+ e₃, f₃=e₂- e₃, e₁, e₂, e₃ - ортонормированный базис, если матрица линейного оператора A евклидова пространства в базисе f₁, f₂, f₃ равна .

131. Задана билинейная форма g(x,y) в пространстве R³ в стандартном базисе e₁, e₂, e₃. Найти ее матрицу в базисе f₁, f₂, f₃. g(x,y)=x₁y₂+x₂y₃+x₃y₁, f₁=(1,0,0), f₂=(1,1,0), f₃=(1,1,1).

132. Привести квадратичную форму f = 3x₂² + 3x₃² + 4x₁x₂ + 4x₁x₃ - 2x₂ x₃к каноническому виду методом Лагранжа и методом собственных преобразований.

133. Привести данные квадратичные формы к каноническому виду методом Лагранжа и записать преобразования переменных.f = x₁² + x₁x₂ + x₃x₄

134. Привести данные квадратичные формы к каноническому виду ортогональными преобразованиями переменных и записать преобразования переменных. f = 2x₁x₂ + 2x₃x₄ .

135. Является ли данная квадратичная форма знакоопределенной. f = 4x₁² + 2x₁x₂ - 2x₁x₃ - 2x₂x₃ + 2x₃².

136. Составить уравнение и построить поверхности вращения: прямой z = y, x =0 вокруг оси Ox.

137. Составить уравнения конуса и построить конусы, если задана вершина S₀ и уравнение ее направляющей. 1)M₀(0,0,0),

138. Установить тип заданных поверхностей и построить их:

139. Установить тип заданных поверхностей и построить их:

140. Найти собственные значения и собственные векторы матрицы.

141. Привести квадратичную форму f = x₁² + 2x₂² + 3x₃² + 2x₁x₂ + 2x₁x₃ + 4x₂ x₃ к каноническому виду методом Лагранжа.

142. Привести квадратичную формы к каноническому виду ортогональными преобразованиями переменных. f = -3x₁² + 9x₂² + 2x₁x₂ + 8x₁x₃+ 4x₂x₃ + 3x₃².

Исследовать кривую второго порядка и построить ее x² + y² - 4xy + 4x - 2y + 1 = 0.