§2. Послідовність. Границя послідовності.

Функція, задана на множині натуральних чисел, називається числовою послідовністю.

Позначається де– загальний член послідовності. Кожна числова послідовність вважається заданою, якщо вказано правило чи закон її утворення.

Наприклад, нехай задано загальний член послідовності , тоді її членами будуть числа. Для послідовностей з загальними членами,членами будуть відповідно числа:та

Приклад 2.1. Побудувати числову послідовність для знаходження грошових накопичень з урахуванням складних процентів.

Розв'язок. Нехай початкова сума вкладу складає грн., процентна ставка дорівнюєрічних. Величинаназивається питомою процентною ставкою.

На кінець першого року сума вкладу складе , на кінець другого року –, на кінецьроку –.

Розглянемо послідовності і. Побудуємо точки на числовій осі, що відповідають членам цих послідовностей:

З рисунку видно, що члени послідовності по мірі зростання номеранаближаються до точки 0, члени другої послідовності необмежено віддаляються від початку координат.

Виберемо - окіл точки 0 з. Поза цим околом знаходяться десять перших членів, всі інші, тобто всі починаючи з номера, належать цьому околу. Виберемо менший окіл точки 0, наприклад. Поза цим околом знаходяться перші сто членів, а всі інші, починаючи з номера, належать вибраному околу.

Означення 1. Число називається границею числової послідовності, якщо будь-який- окіл точкимістить всі члени послідовності, починаючи з деякого номера, а поза ним знаходиться фіксоване число членів послідовності.

Якщо члени послідовності належать - околу точки, то це значить, що для всіх цих членів виконується нерівність, або згідно властивості 7 модуля.

Означення 2. Число називається границею числової послідовності, якщо для будь-якогоіснує такий номер, що для всіх членів послідовності з номерамивиконується нерівність

. ( 2.1 )

Границя числової послідовності позначається або.

Приклад 2.2 Довести, що для послідовності ,.

Розв'язування. Для будь-якого нерівність ( 2.1 )абовиконується при. Отже, при будь-якомуіснує такий номер( або рівний цілій частині), що для всіхвиконується нерівність. А це означає, що.

Приклад 2.3 Довести, що послідовність не має границі.

Розв’язування. При будь-якому два сусідні члени цієї послідовності відрізняються за модулем на 2. Отже дляна числовій осі не має жодної точки- окіл якої містив би усі члени послідовності починаючи з деякого. Це означає, що ні одне дійсне число не може бути границею цієї послідовності.

Послідовності, які мають границю, називаються збіжними, а ті що не мають – розбіжними.

Обмежені послідовності. Зв'язок між існуванням границі та її обмеженістю.

Означення. Послідовність називається обмеженою, якщо існує таке число, що для всіхвиконується нерівність.

Теорема. Якщо послідовність має границю, то вона обмежена.

Доведення. Нехай . Дляіснує номер такий номер, що для всіх членів послідовності з номерамивиконується нерівність. Виберемо. Тоді для всіхвиконується нерівність, а отже послідовністьє обмеженою.

Зауважимо, що протилежне твердження в цілому не вірне. Наприклад, послідовність обмежена, але границі не має.

Нескінченно малі послідовності та їх властивості.

Означення. Послідовність називається нескінченно малою, якщо її границя дорівнює нулю.

Властивості нескінченно малих послідовностей:

1. Алгебраїчна сума фіксованого числа нескінченно малих послідовностей є нескінченно мала послідовність.

2. Добуток нескінченно малої послідовності на обмежену послідовність ( в тому числі на сталу, іншу нескінченно малу послідовність ) є нескінченно мала послідовність.

Властивості границь.

Властивість 1. Якщо всі члени послідовності дорівнюють , то і границя цієї послідовності дорівнює .

Властивість 2. Якщо послідовність має границю, то послідовність – нескінченно мала.

Властивість 3. Якщо послідовність має границю, то вона єдина.

Нескінченно великі послідовності, зв'язок з нескінченно малими.

Означення. Послідовність називається нескінченно великою, якщо длязнайдеться номер, починаючи з якого правильна нерівність.

Приклад 2.4. Довести, що послідовність ,нескінченно велика.

Розв’язування. Нехай , тобто. Длявиконується нерівність. Візьмемо. Тоді дляправильна нерівність.

Теорема. Якщо послідовність – нескінченно мала, то послідовність,– нескінченно велика, і навпаки, якщо послідовність– нескінченно велика, то послідовність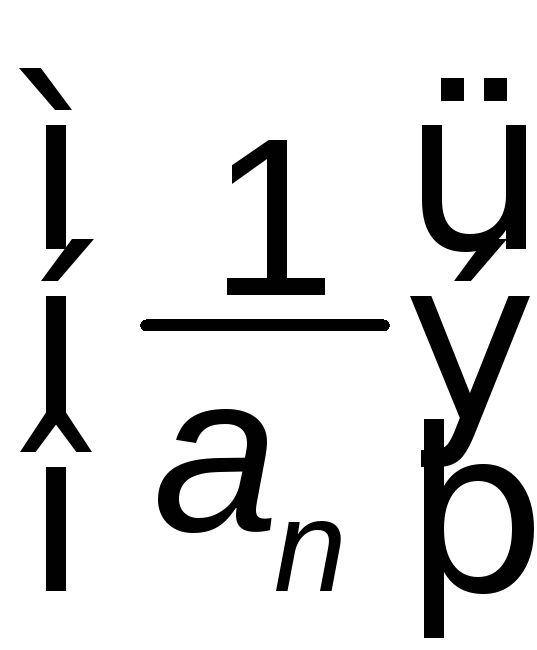– нескінченно мала.

Основні теореми про границю.

Відмітимо в першу чергу арифметичні теореми про границю послідовності:

Теорема. Нехай , а. Тоді

1)

2)

3) , якщоі.

Крім арифметичних теорем важливе значення мають і теореми порівняння:

Теорема 1. Нехай і для,, тоді і.

Теорема 2. Нехай ,і для,, тоді і.

Теорема 3. Якщо і, то починаючи з деякого номераі всі члени послідовності зберігають знак границі.

Слід зауважити, що теореми 1, 2 справедливі і в тому випадку, коли умови ,виконуються починаючи з деякого номера.

Монотонні послідовності. Ознаки існування границі.

Означення. Послідовність називається зростаючою (неспадною, спадною, незростаючою) якщо длявиконується умова(,,).

Зростаючі, спадні, неспадні та незростаючі послідовності називаються монотонними, а зростаючі і спадні – строго монотонними.

Не завжди зручно для з'ясування питання про існування границі послідовності використовувати означення границі. Простіше це зробити за допомогою ознак існування границі.

Теорема 1 (Вейєрштрасса). Якщо послідовність монотонна і обмежена, то вона має границю.

Дану теорему використовують для доведення існування границі послідовності . Цю границю прийнято позначати буквою:. Можна довести, що число– ірраціональне,. Число( число Ейлера ) відіграє важливу роль в математичному аналізі. Широко використовують логарифми за основою, які називають натуральними. Числоз'являється і в деяких економічних задачах.

Теорема 2. Якщо ,і для,, тоді і.

Завдання для самостійного розв’язування.

2.1 Скориставшись означенням границі довести, що

а) . б).

2.2 Впевнитись, що послідовність не має границі при необмеженому зростанні.