
3. Означення границі функції і її властивості.
Розглянемо приклади, що розкривають зміст поняття границі функції.
Приклад
3.1. Розглянемо
функцію
![]() в деякому околі точки
в деякому околі точки![]() .
З цього околу виберемо довільну
послідовність аргументу
.
З цього околу виберемо довільну
послідовність аргументу![]() ,
наприклад
,
наприклад![]() .
Обчисливши значення функції
.
Обчисливши значення функції![]() для кожного члена послідовності, одержимо
послідовність відповідних значень
для кожного члена послідовності, одержимо
послідовність відповідних значень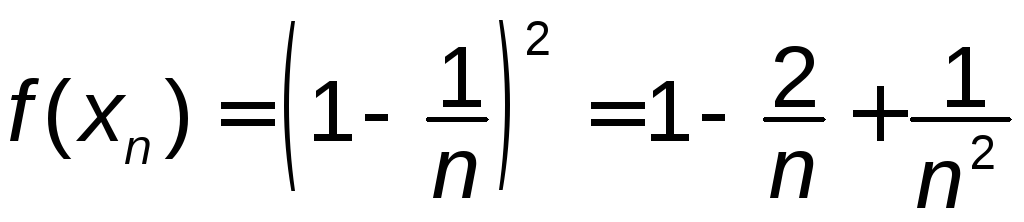 .
Очевидно
.
Очевидно![]() .
Виберемо іншу послідовність значень
аргументу
.
Виберемо іншу послідовність значень
аргументу![]() з того ж самого околу, наприклад,
з того ж самого околу, наприклад,![]() .
Складена для неї послідовність відповідних
значень заданої функції має вигляд:
.
Складена для неї послідовність відповідних
значень заданої функції має вигляд: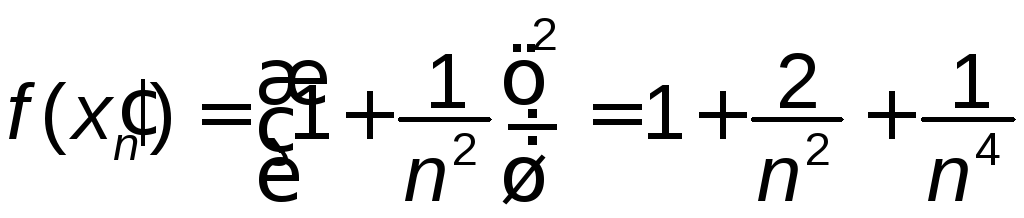 .
Очевидно
.
Очевидно![]() .
Отже, для довільних послідовностей
аргументу
.
Отже, для довільних послідовностей
аргументу![]() послідовність
послідовність![]() відповідних значень заданої функції
відповідних значень заданої функції![]() має одну і ту ж границю 1.
має одну і ту ж границю 1.
Приклад
3.2.
Розглянемо
функцію
![]() в околі радіуса 1 якої-небудь цілої
точки, наприклад,
в околі радіуса 1 якої-небудь цілої
точки, наприклад,![]() .
Виберемо в лівому півоколі довільну
послідовність
.
Виберемо в лівому півоколі довільну
послідовність![]() ,
наприклад,
,
наприклад,![]() .
Очевидно
.
Очевидно![]() для будь-якого
для будь-якого![]() .
Складемо для неї послідовність відповідних
значень заданої функції. Одержимо
послідовність
.
Складемо для неї послідовність відповідних
значень заданої функції. Одержимо
послідовність![]() ,
яка має границю 0. Виберемо тепер в
правому півоколі довільну послідовність
,
яка має границю 0. Виберемо тепер в
правому півоколі довільну послідовність![]() ,
наприклад,
,
наприклад,![]() .
Очевидно
.
Очевидно![]() для будь-якого
для будь-якого![]() .
Складемо для неї послідовність відповідних
значень заданої функції. Одержимо
послідовність
.
Складемо для неї послідовність відповідних
значень заданої функції. Одержимо
послідовність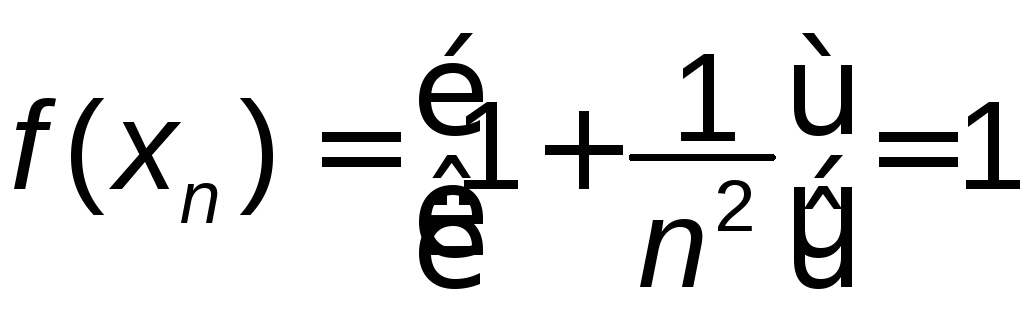 ,
яка має границю 1. Таким чином, на відміну
від попереднього прикладу для різних
послідовностей аргументу, що мають
границю 1, послідовності відповідних
значень функції
,
яка має границю 1. Таким чином, на відміну
від попереднього прикладу для різних
послідовностей аргументу, що мають
границю 1, послідовності відповідних
значень функції![]() ,
,![]() мають різні границі.
мають різні границі.
Означення
1 (
за Гейне ). Нехай функція
![]() визначена в деякому околі точки
визначена в деякому околі точки![]() ,
за винятком, можливо, самої точки
,
за винятком, можливо, самої точки![]() .
Число
.
Число![]() називається границею функції
називається границею функції![]() при
при![]() (або в точці
(або в точці![]() ),
якщо для будь-якої послідовності
аргументів
),
якщо для будь-якої послідовності
аргументів![]() і такої, що
і такої, що![]() ,
відповідна послідовність
,
відповідна послідовність![]() значень функції має одну і ту ж границюА.
значень функції має одну і ту ж границюА.
Символічний
запис: ![]() .
.
Як
приклад,
![]() ,
а функція
,
а функція![]() не має границі в точці
не має границі в точці![]() .
.
Для доведення деяких властивостей функцій, що мають границю, використовують означення границі функції за Коші:
Означення
2.
Число
![]() називається границею функції
називається границею функції![]() при
при![]() ,
якщо для
,
якщо для![]() існує число
існує число![]() таке, що з нерівностей
таке, що з нерівностей![]() випливає нерівність
випливає нерівність![]() .
.
Можна довести, що означення границі функції за Коші і Гейне рівносильні.
Означення.
Число
![]() називається лівою (правою) границею
функції
називається лівою (правою) границею
функції![]() при
при![]() ,
якщо для будь-якої послідовності
аргументів
,
якщо для будь-якої послідовності
аргументів![]() і такої, що
і такої, що![]() ,
відповідна послідовність
,
відповідна послідовність![]() значень функції має одну і ту ж границю
значень функції має одну і ту ж границю![]() .
.
Позначення:
![]() ,
,![]() .
.
Ліва
і права границі називаються односторонніми
границями. Очевидно, для того щоб функція
![]() при
при![]() мала границю, необхідно і достатньо щоб
вона мала ліву і праву границі при
мала границю, необхідно і достатньо щоб
вона мала ліву і праву границі при![]() і вони були рівні.
і вони були рівні.
Властивості функцій, що мають границю.
Теорема
1. (про
обмеженість). Якщо функція
![]() має границю
має границю![]() при
при![]() ,
то в деякому околі точки
,
то в деякому околі точки![]() вона обмежена.
вона обмежена.
Теорема
2. (про
збереження знаку ). Якщо функція
![]() має границю
має границю![]() при
при![]() ,
то в деякому околі точки
,
то в деякому околі точки![]() функція зберігає знак границі.
функція зберігає знак границі.
Зауважимо,
що обидві теореми носять локальний
характер, тобто виконуються для точок,
що лежать поблизу точки
![]() .
.
Також слід зауважити, що для границі функції справедливі арифметичні теореми і теореми порівняння, аналогічні відповідним теоремам про границю послідовності.
Розкриття невизначеностей.
При знаходженні границь функцій (послідовностей) ми користуємось арифметичними теоремами в припущенні, що відповідні границі існують, а для частки з додатковою умовою, що границя знаменника відміна від нуля.
В
деяких випадках, що залишились без
розгляду ( коли границі функцій ( одна
або обидві ) нескінченні чи не існують,
або у випадку частки - границя знаменника
дорівнює нулю ) можна цілком визначено
сказати як поводить себе відповідна
функція. Наприклад, якщо
![]() ,
,![]() ,
,![]() ,
то
,
то![]() ,
,![]() ,
,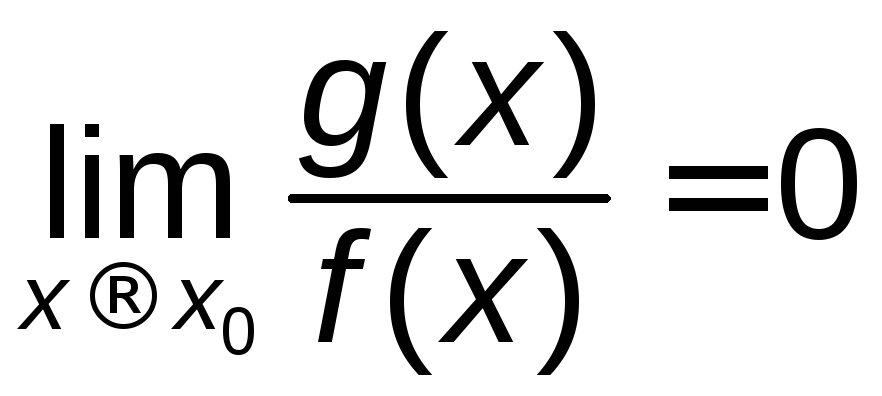 ,
, .
.
Проте,
якщо
![]() ,
то про границю частки
,
то про границю частки![]() ніякого загального твердження ми зробити
не можемо. Наприклад, нехай
ніякого загального твердження ми зробити
не можемо. Наприклад, нехай![]() ,
,![]() .
Обидві функції при
.
Обидві функції при![]() прямують до нуля. Їх відношення
прямують до нуля. Їх відношення також прямує до нуля, коли
також прямує до нуля, коли![]() .
Якщо ж, навпаки,
.
Якщо ж, навпаки,![]() ,
,![]() ,
то
,
то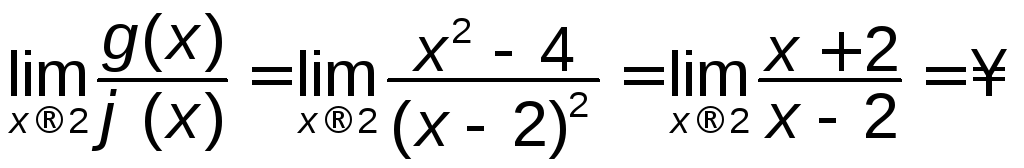 .
Отже, в залежності від вигляду обох
функцій, границя частки може існувати,
а може і не існувати. В зв’язку з цим
говорять, що мають справу з невизначеністю.
А задача знаходження границі в кожному
такому випадку називається задачею
розкриття невизначеності. Розглянемо
найбільш важливі випадки:
.
Отже, в залежності від вигляду обох
функцій, границя частки може існувати,
а може і не існувати. В зв’язку з цим
говорять, що мають справу з невизначеністю.
А задача знаходження границі в кожному
такому випадку називається задачею
розкриття невизначеності. Розглянемо
найбільш важливі випадки:
а)
невизначеність
![]() .
.
Якщо
![]() і
і![]() ,
то у випадку знаходження границі частки
,
то у випадку знаходження границі частки![]() ми маємо невизначеність
ми маємо невизначеність![]() .
У випадку, коли функції
.
У випадку, коли функції![]() та
та![]() є алгебраїчними, то для розкриття
невизначеності в чисельнику і знаменнику
слід виділити множник
є алгебраїчними, то для розкриття
невизначеності в чисельнику і знаменнику
слід виділити множник![]() ,
щоб в подальшому скоротити дріб на цей
множник:
,
щоб в подальшому скоротити дріб на цей
множник:
1)
 .
.
2)
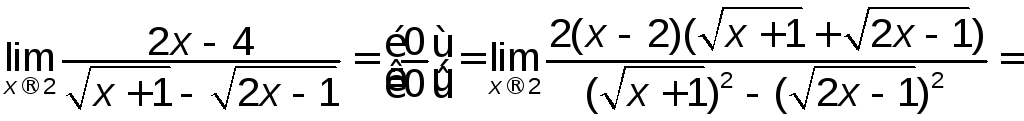
 .
.
В
другому прикладі для виділення множника
![]() знищили ірраціональність в знаменнику
шляхом домноження на спряжений вираз.
знищили ірраціональність в знаменнику
шляхом домноження на спряжений вираз.
б)
невизначеність
![]() .
.
Нехай
![]() ,
,![]() при
при![]() .
В цьому випадку вираз
.
В цьому випадку вираз![]() називають невизначеністю
називають невизначеністю![]() .
Як приклад розглянемо відношення двох
многочленів. Вираз
.
Як приклад розглянемо відношення двох
многочленів. Вираз![]() ,
,![]() ,
,![]() - ціле невід'ємне число, називається
многочленом . Перший доданок
- ціле невід'ємне число, називається
многочленом . Перший доданок![]() називається старшим членом,
називається старшим членом,![]() - степенем многочлена. Поведінка
многочлена, коли
- степенем многочлена. Поведінка
многочлена, коли![]() визначається поведінкою старшого члена,
тобто
визначається поведінкою старшого члена,
тобто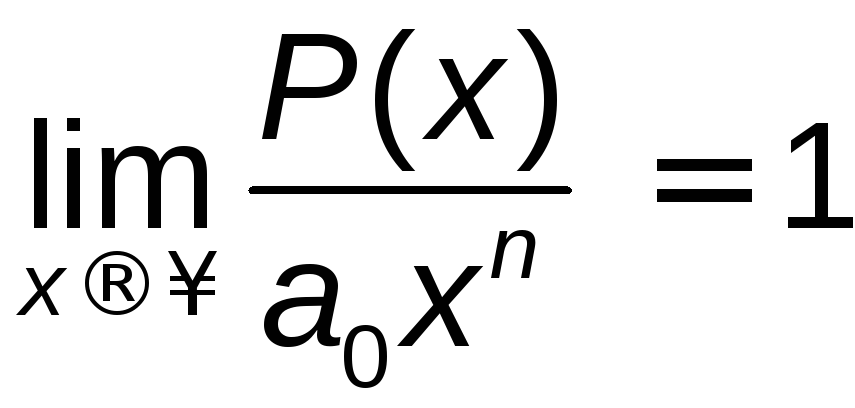 .
Тому:
.
Тому:
1) 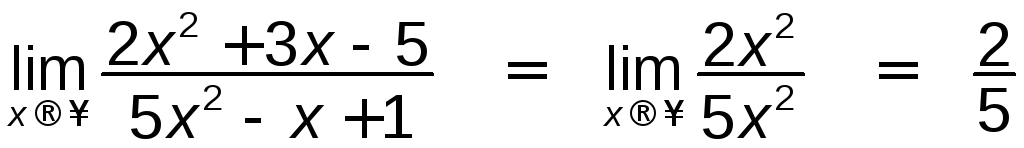 ,
,
2) 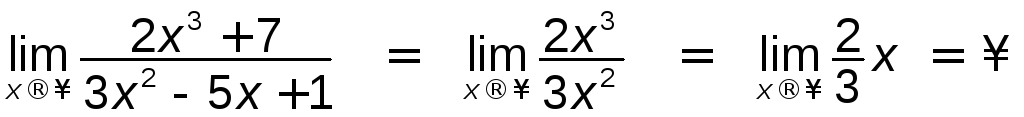 ,
,
3)  .
.
Наведені приклади можна об'єднати в загальне правило:
границя
відношення двох многочленів дорівнює
![]() ,
якщо степінь чисельника більший степеня
знаменника; дорівнює 0, якщо степінь
чисельника менший степеня знаменника,
і дорівнює відношенню коефіцієнтів при
старших членах, якщо степені чисельника
і знаменника рівні, тобто
,
якщо степінь чисельника більший степеня
знаменника; дорівнює 0, якщо степінь
чисельника менший степеня знаменника,
і дорівнює відношенню коефіцієнтів при
старших членах, якщо степені чисельника
і знаменника рівні, тобто
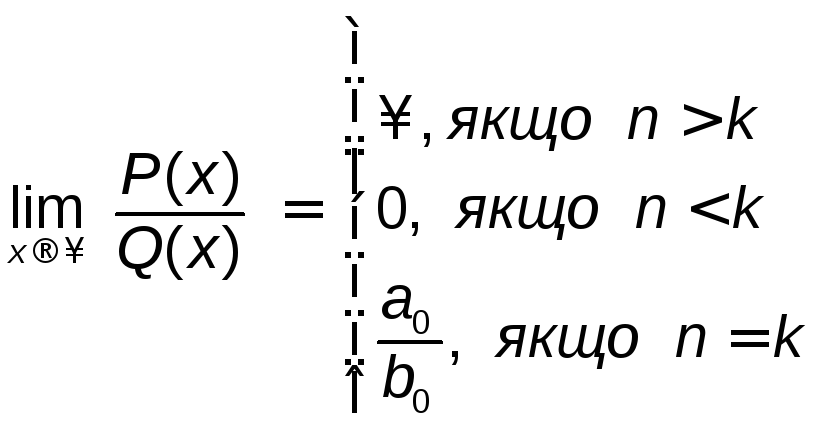 ,
,
де
![]() степені многочленів
степені многочленів![]() відповідно.
відповідно.
в)
невизначеність
![]() .
.
Нехай
![]() ,
,![]() при
при![]() .
Тоді вираз
.
Тоді вираз![]() дає невизначеність
дає невизначеність![]() .
Щоб розкрити невизначеність такого
вигляду, потрібно звести її до
невизначеностей вигляду
.
Щоб розкрити невизначеність такого
вигляду, потрібно звести її до
невизначеностей вигляду![]() або
або![]() .
.
Приклад
3.3
Знайти
![]() .
.
Розв’язування.
![]()
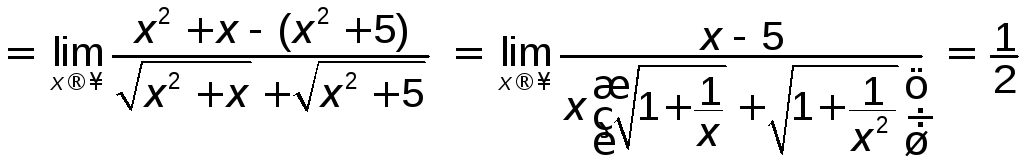 .
.
г)
невизначеність
![]() .
.
Розглянемо
![]() .
Якщо
.
Якщо![]() ,
,![]() при
при![]() ,
то вираз
,
то вираз![]() дає невизначеність
дає невизначеність![]() .
Щоб розкрити невизначеність даного
вигляду, як і у попередньому випадку
слід звести її до невизначеностей
вигляду
.
Щоб розкрити невизначеність даного
вигляду, як і у попередньому випадку
слід звести її до невизначеностей
вигляду![]() або
або![]() .
.
Завдання для самостійного розв’язування.
3.1 Знайти границі:
а)
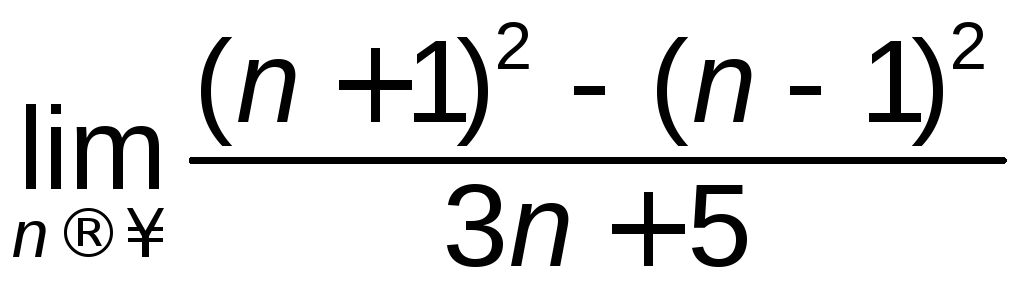 ; б)
; б) ;
;
в)
 ; г)
; г) ;
;
д)
 ; е)
; е)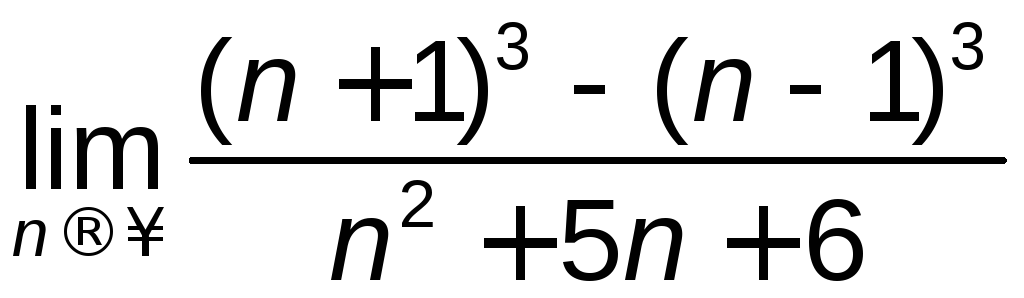 .
.
3.2 Знайти границі:
а)
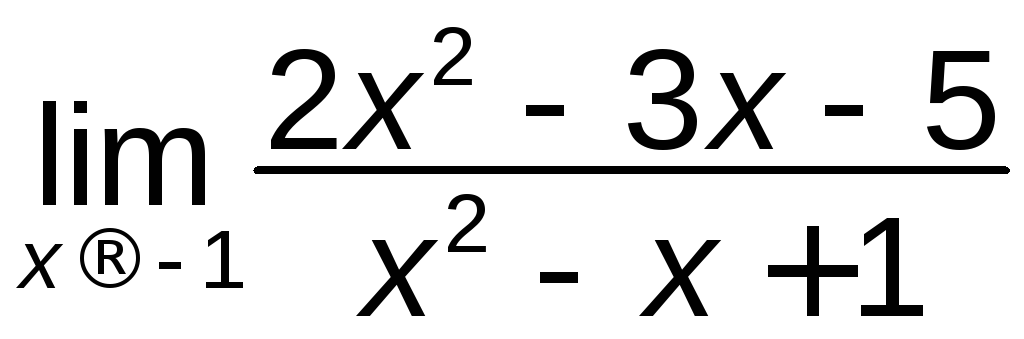 ; б)
; б)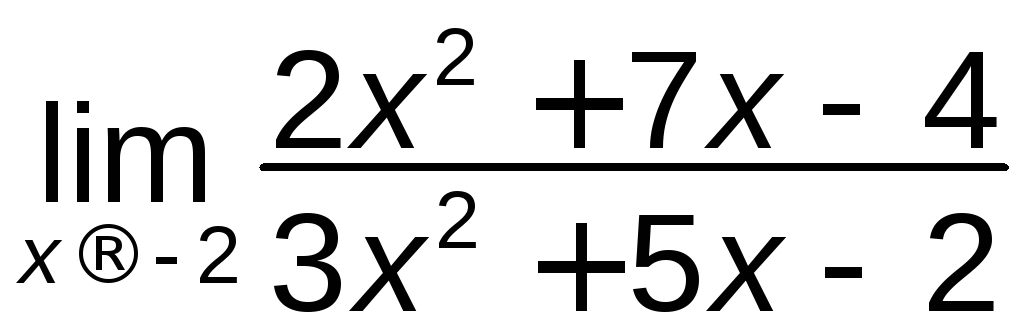 ;
;
в)
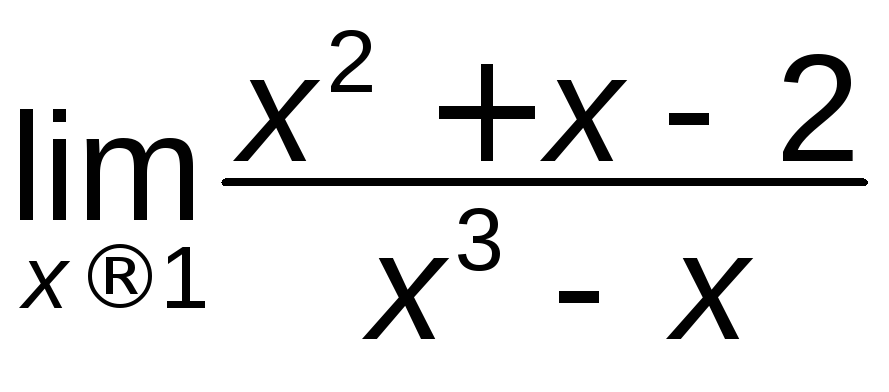 ; г)
; г)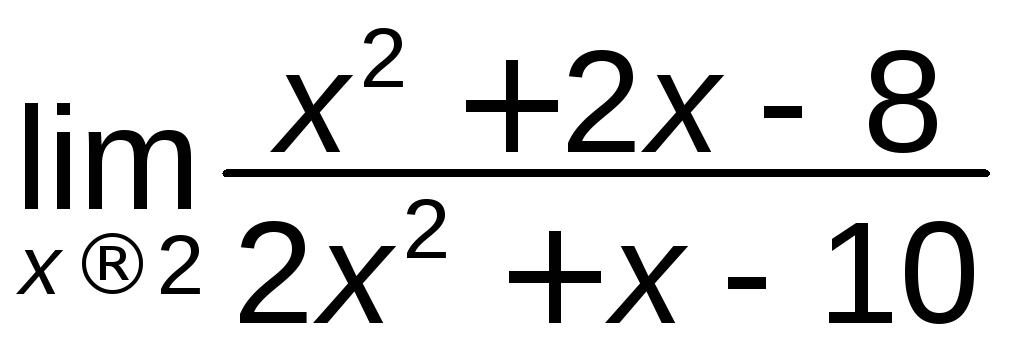 ;
;
д).
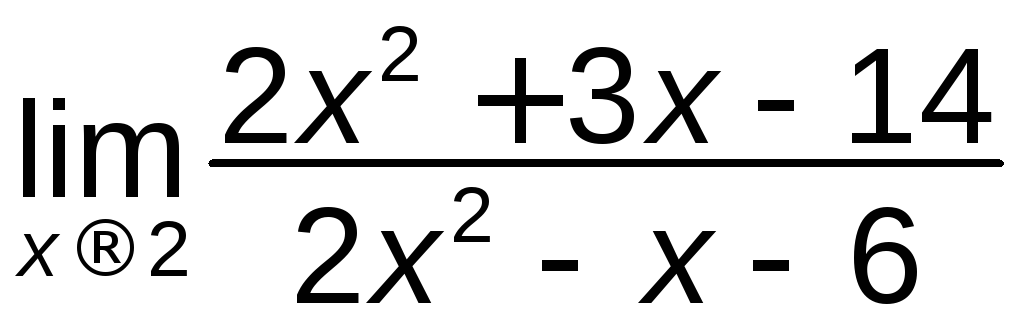 ; е)
; е)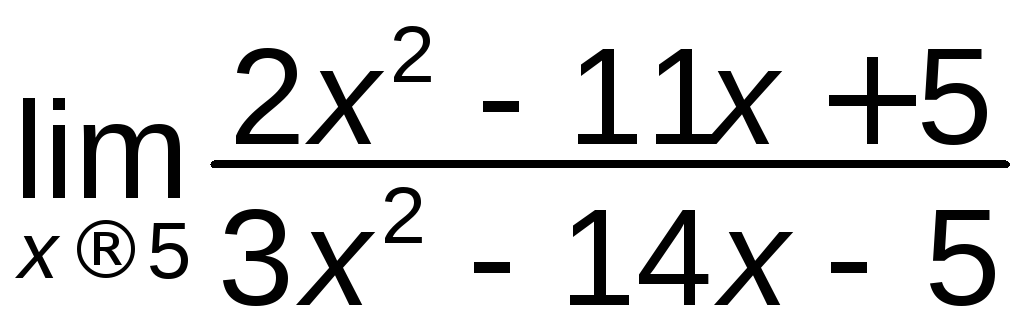 .
.
3.3 Знайти границі:
а)
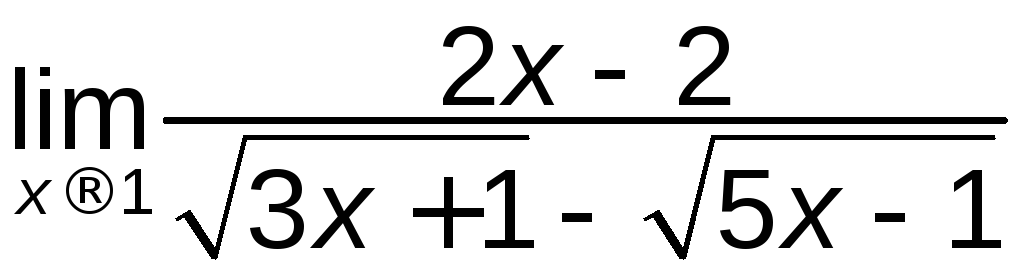 ; б)
; б)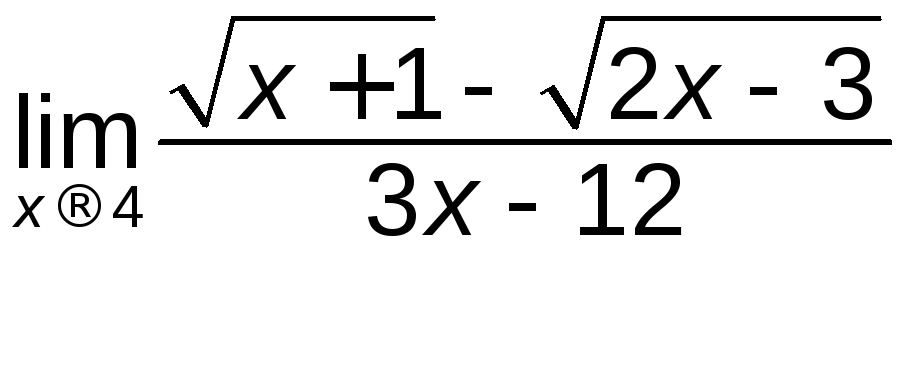 ;
;
в)
 ; г)
; г)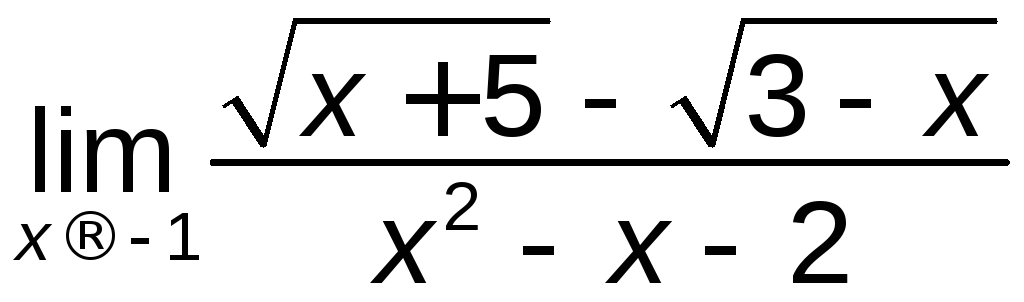 ;
;
д)
 ; е)
; е)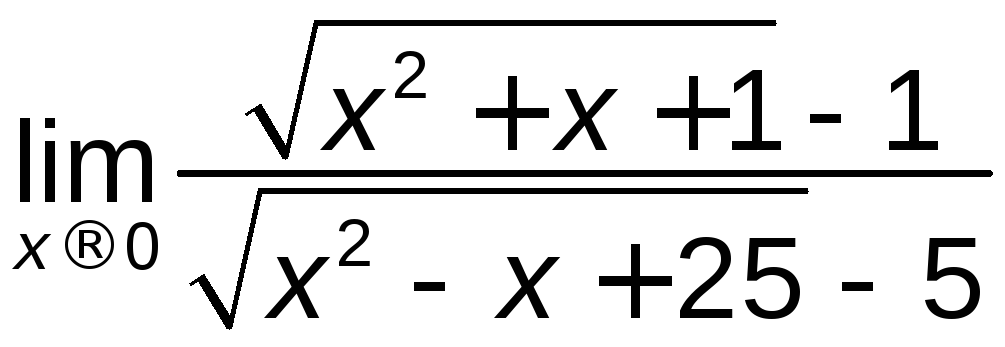 ;
;
є)
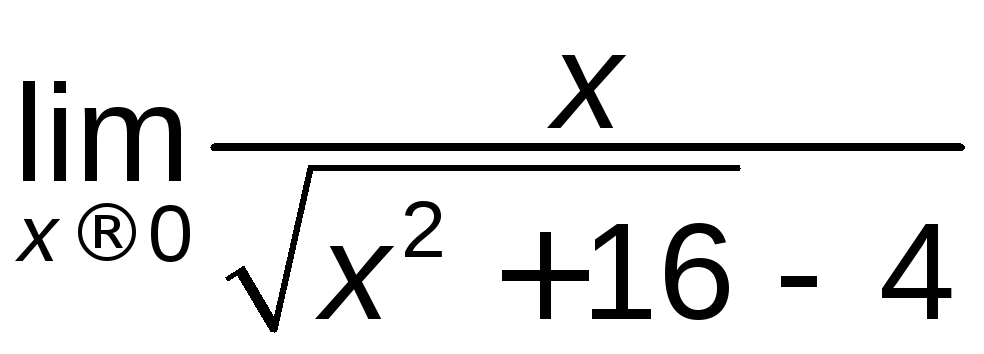 ; ж)
; ж)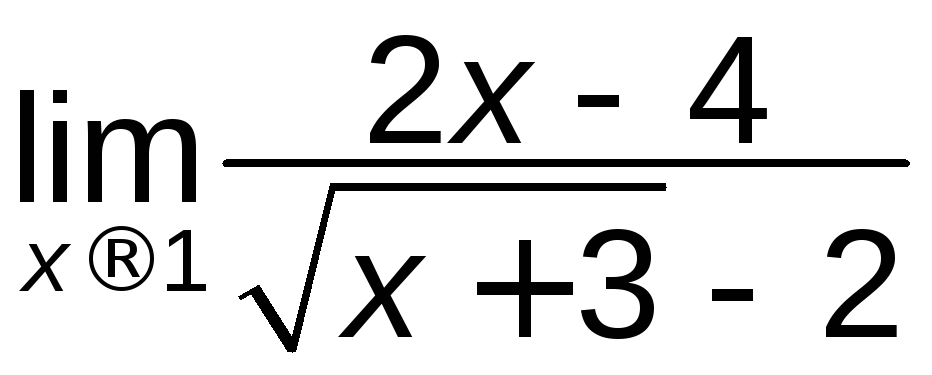 .
.
3.4 Знайти границі:
а)
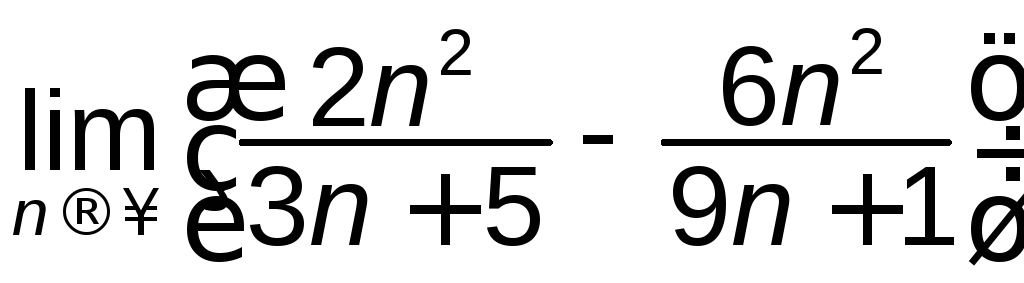 ; б)
; б)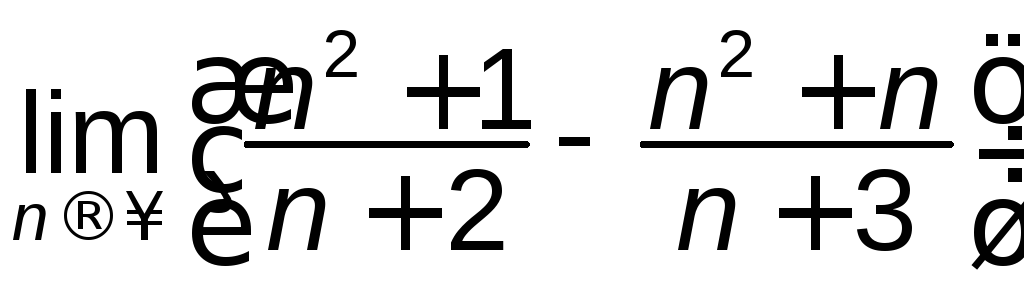 ;
;
в)
![]() ; г)
; г)![]() ;
;
д)
![]() ; е)
; е)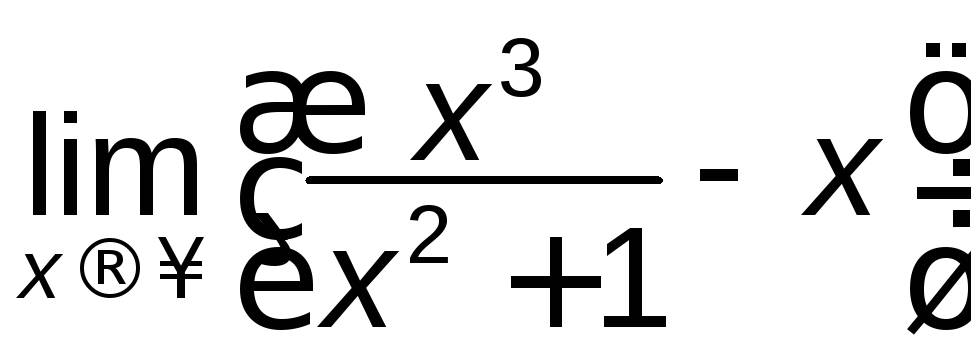 .
.
Відповіді:
3.1
а)
![]() б)
б)
![]() в)
в)![]() г)
г)![]() д)
0; е)
6;
д)
0; е)
6;
3.2
а) 0; б)
![]() ; в)
; в)
![]() ; г)
; г)![]() д)
д)
![]() е)
е)![]()
3.3
а)
![]() ; б)
; б)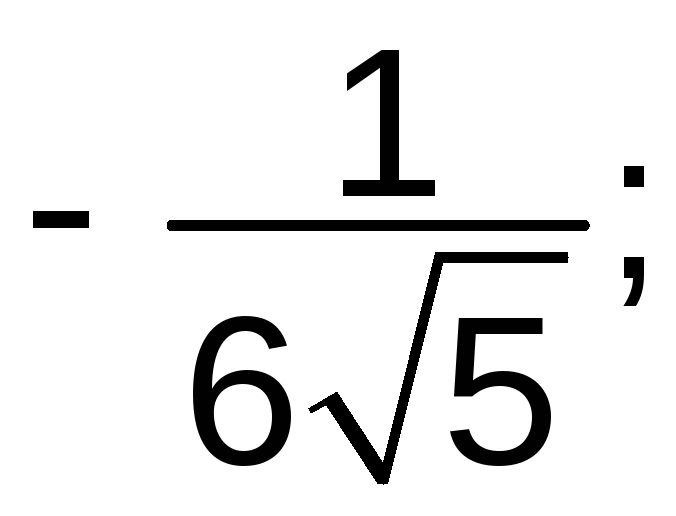 в)
в)![]() г)
г)![]() д)
д)
![]() е)
-5;
е)
-5;
є)
![]() ; ж)
; ж)
![]() ;
;
3.4
а)
![]() б)
б)![]() в)
в)![]() г)
г)![]() д)
-1; е) 0;
д)
-1; е) 0;
Чудові границі.
1)
В попередньому параграфі було встановлено,
що
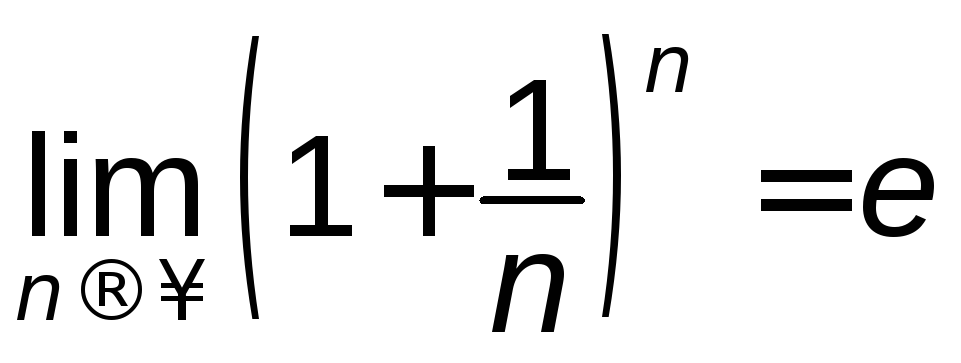 .
Розглянемо функцію
.
Розглянемо функцію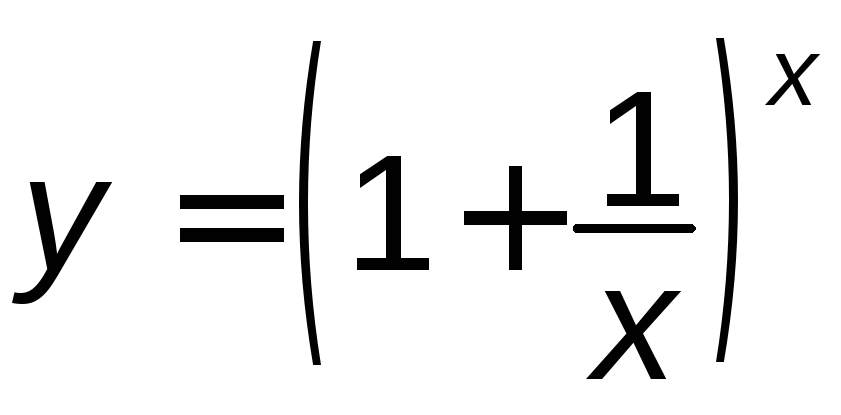 .
Ця функція існує для всіх
.
Ця функція існує для всіх![]() крім
крім![]() .
Можна довести, що
.
Можна довести, що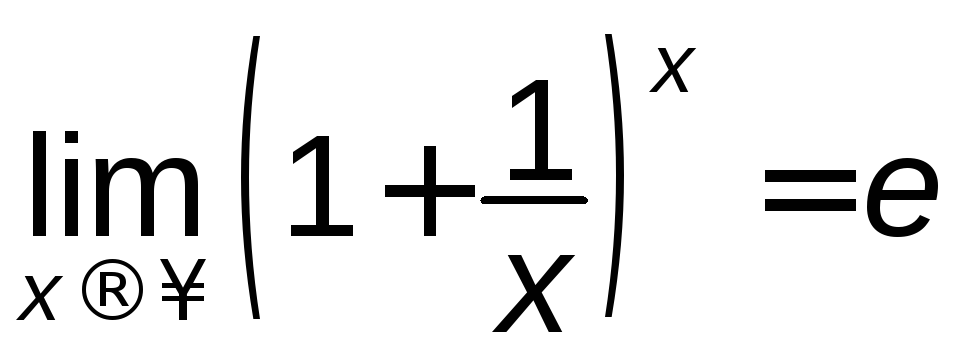 .
Слід звернути увагу на те, що основа
степеня
.
Слід звернути увагу на те, що основа
степеня![]() при
при![]() ,
а показник степеня
,
а показник степеня![]() .
Тобто вираз
.
Тобто вираз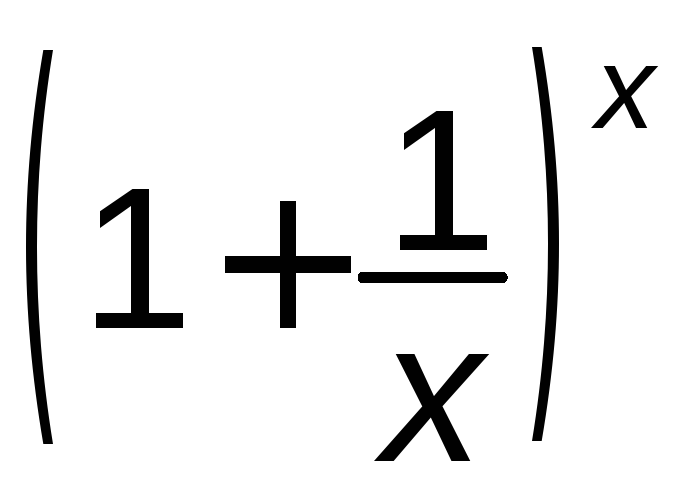 дає невизначеність
дає невизначеність![]() .
.
Поклавши
![]() ,
знайдемо
,
знайдемо![]() . При
. При![]()
![]() .
У результаті отримаємо ще один запис
числа
.
У результаті отримаємо ще один запис
числа![]() :
:![]() .
Обидва розглянутих співвідношення
носять назву першої чудової границі і
можуть бути використані для розкриття
невизначеності
.
Обидва розглянутих співвідношення
носять назву першої чудової границі і
можуть бути використані для розкриття
невизначеності![]() .
На практиці широко використовують
формулу:
.
На практиці широко використовують
формулу:
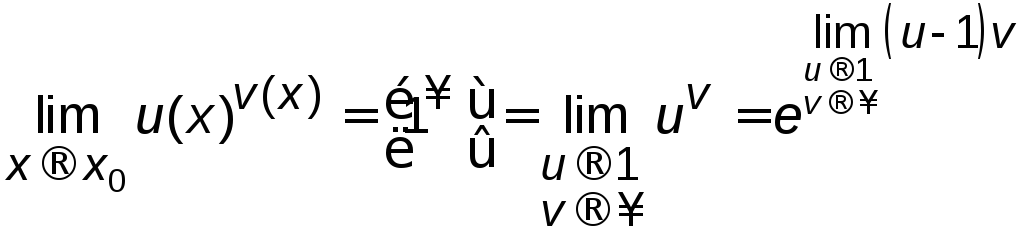
Приклад 3.4 Знайти:
а)
 ; б)
; б) .
.
Розв’язування.
а)
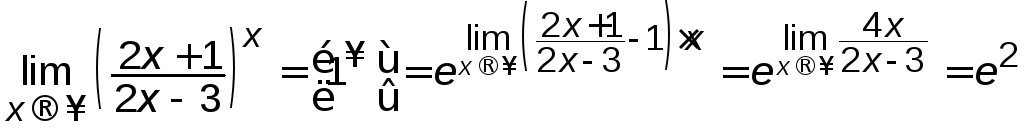 .
.
б)
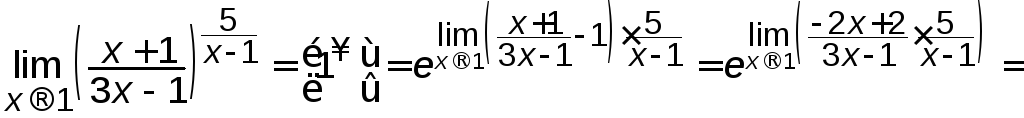
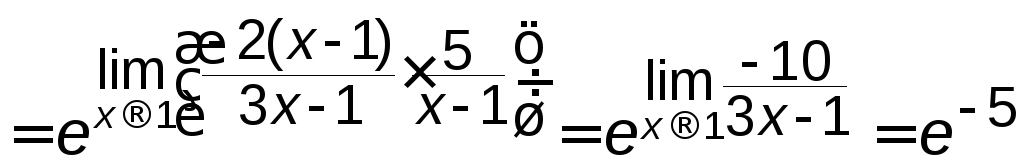 .
.
2)
Другою чудовою границею називається
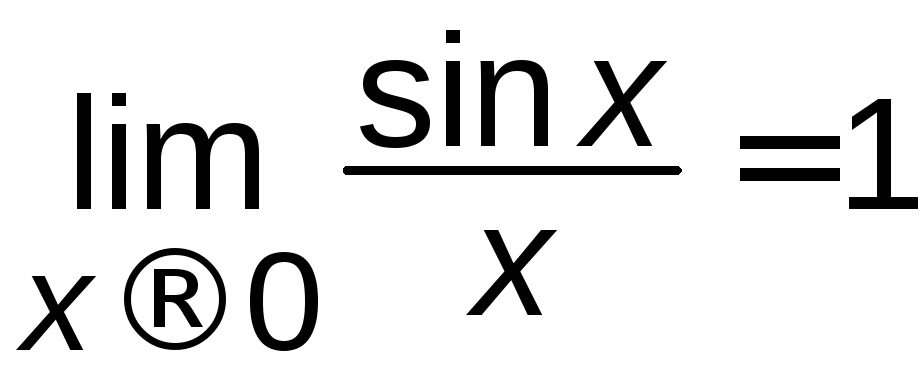 .
Скориставшись даним співвідношенням,
можна довести, що
.
Скориставшись даним співвідношенням,
можна довести, що
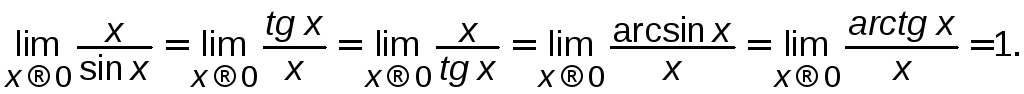
В
усіх цих співвідношеннях розглядається
відношення двох нескінченно малих
величин при умові, що
![]() .
Отже всі вони можуть бути використані
для розкриття невизначеностей
.
Отже всі вони можуть бути використані
для розкриття невизначеностей![]() ,
в яких містяться тригонометричні або
обернені тригонометричні функції.
,
в яких містяться тригонометричні або
обернені тригонометричні функції.
Приклад 3.5 Знайти
а)
![]() ; б)
; б) .
.
Розв’язування.
а)
 .
.
б)
 .
.
Завдання для самостійного розв’язування.
3.5 Знайти границі:
а)
 ; б)
; б) ;
;
в)
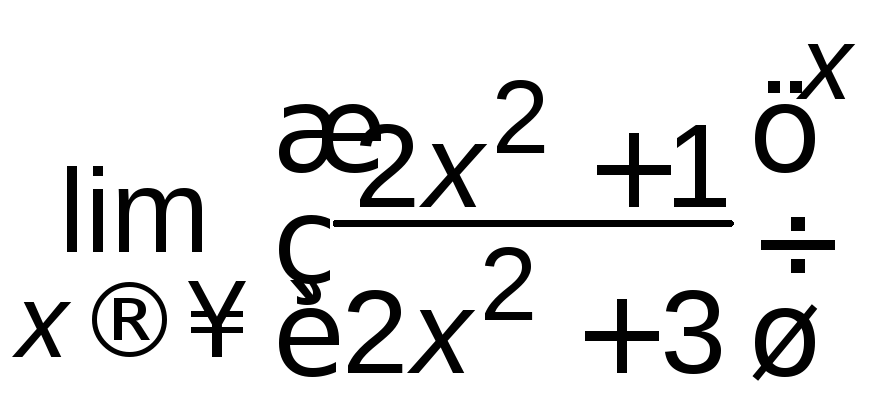 ; г)
; г)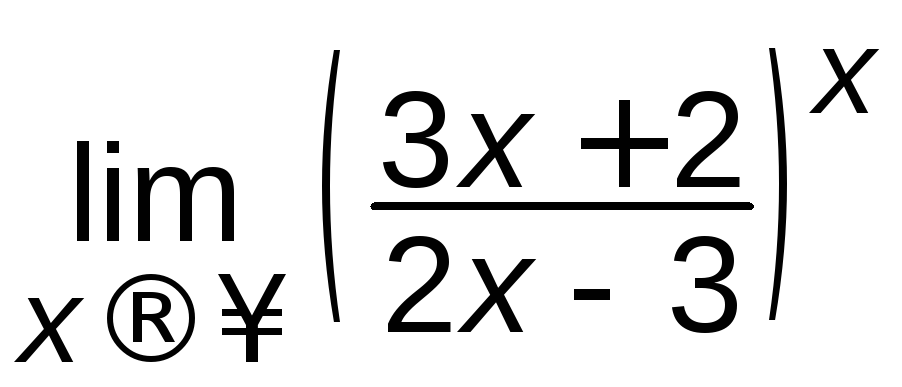 ;
;
д)
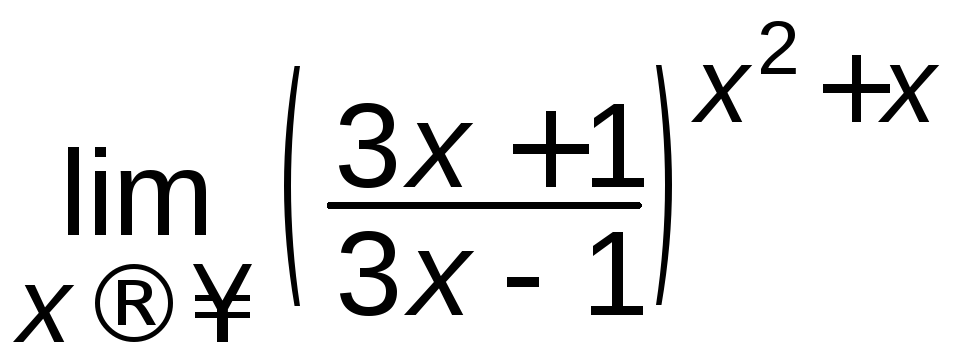 ; е)
; е)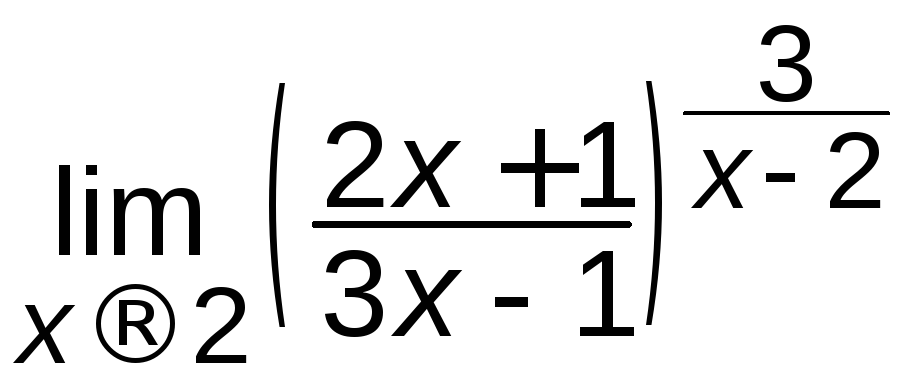 ;
;
є)
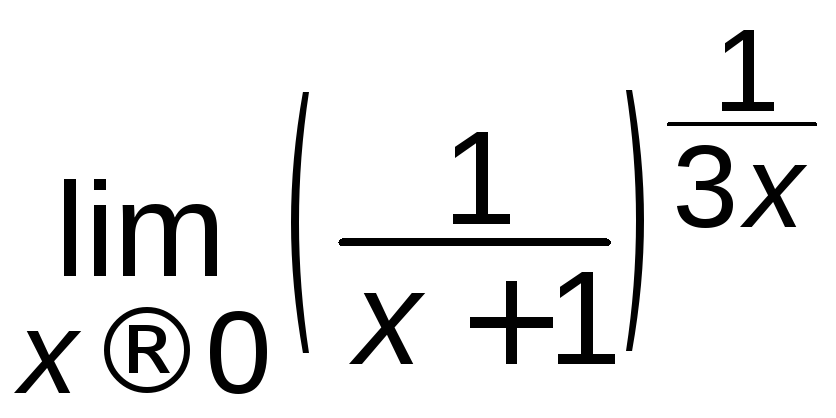 ; ж)
; ж)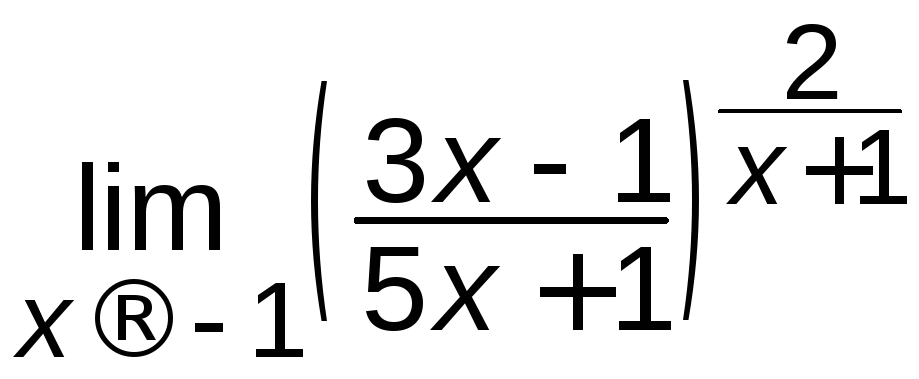 .
.
3.6 Знайти границі:
а)
![]() ; б)
; б)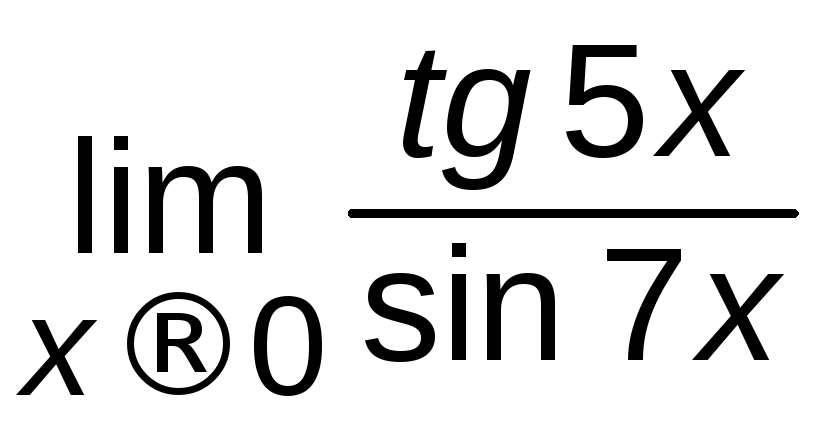 ;
;
в)
 ; г)
; г)![]() ;
;
д).
![]() ; е)
; е)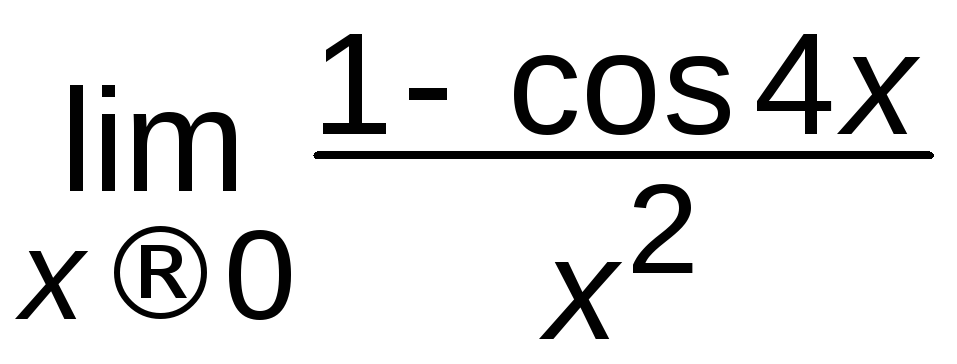 ;
;
є)
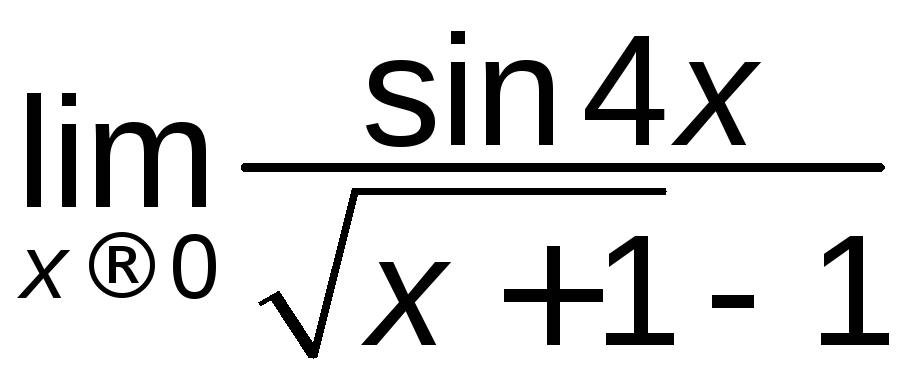 . ж)
. ж)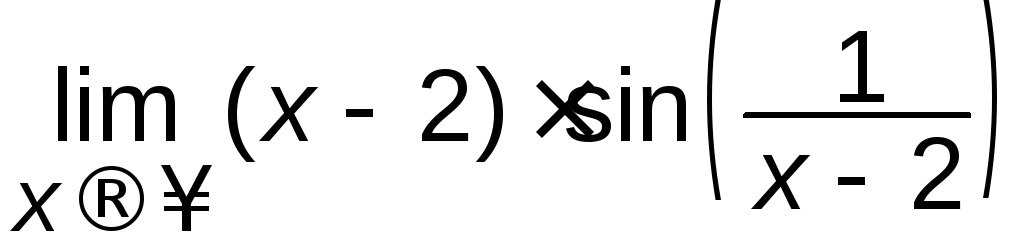 .
.
Відповіді:
3.5 а)
![]() ; б)
; б)
![]() ; в)
1; г)
; в)
1; г)![]() ; д)
; д)
![]() ; е)
; е)![]() ;
;
є)
![]() ; ж)e.
; ж)e.
3.6 а)
![]() ; б)
; б)
![]() ; в)
2; г)
; в)
2; г)![]() ; д)
; д)
![]() ; е)
8;
; е)
8;
є) 8 ; ж) 1.
