§4. Неперервність функції.

З поняттям границі функції тісно пов’язано і інше важливе поняття математичного аналізу – поняття неперервності функції. Інтуїтивно поняття неперервності функції пов’язано з графіком функції: функція вважається неперервною, якщо її графік можна провести лінією, не відриваючи олівця від паперу. Що ж станеться, якщо зробити в якійсь точці "прокол"? Тоді перпендикуляр, проведений з цієї точки на ось абсцис, не перетне графіка функції, що рівносильно відсутності значення функції в цій точці. Отже перший висновок: неперервна функція повинна мати значення в точці . Нехай тепер, підходячи до точкиз різних сторін, ми залишаємось на "різних рівнях". І в цьому випадку, переходячи через точкуми відриваємо олівець від паперу. Раніше говорилось, що для існування границі функції в точцінеобхідно і достатньо, щоб існували обидві односторонні границі, рівні між собою. Таким чином, для неперервності функції необхідно, щоб в точцііснувала границя. Якщо значення функції в точціне співпадатиме з її границею, то функція теж не буде неперервною. Тому зрозумілі умови, які повинні виконуватись для неперервності функції в точці.

Означення 1. Функція називається неперервною в точці, якщо виконуються наступні умови:

1. функція визначена в околі точки , тобто;

2. функція має границю в точці , тобто;

3. ця границя дорівнює значенню функції в точці , тобто.

Приклад 4.1 Дослідити неперервність в точці функцій:

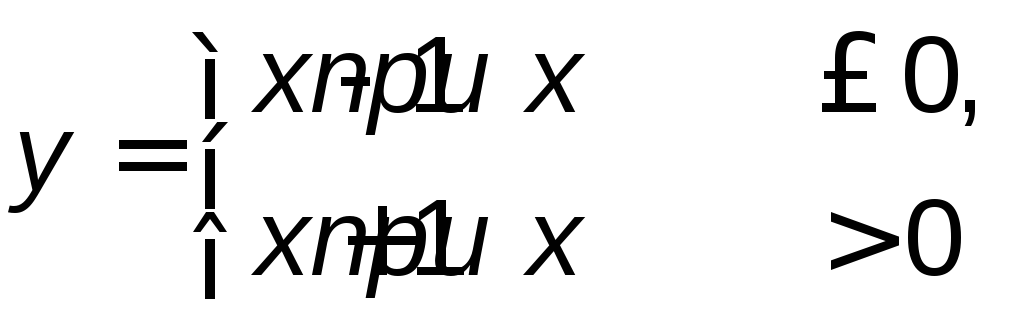а) ; б); в).

Розв’язування.

а) В точці функціяне є неперервною, так як порушується перша умова неперервності – існування.

б) В точці функціяне є неперервною – перша умова неперервності виконується,існує (=1 ), проте порушена друга умова – відсутня( точніше, тут існують односторонні границі функції: лівосторонняі правостороння, проте їх значення не співпадають ).

в) В точці функціянеперервна, так як виконуються всі умови неперервності –.

Означення неперервності функції в точці може бути записано і так:, тобто для неперервної функції можливе переставлення символів границі і функції.

Поняття неперервності можна сформулювати і на мові приростів. Приростом аргументу в точціназивається різниця. Звідки. Приростом функціїв точціназивається різниця.

Означення 2 Функція називається неперервною в точці, якщо вона визначена в цій точці і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції, тобто

.

Приклад 4.2 Довести неперервність функції .

Розв’язування. Розглянемо довільну точку і задамо приріст. Тоді. Знайдемо. Отже за другим означенням неперервності функціянеперервна в довільній точці.

Для функцій, неперервних в точці , справедливі арифметичні теореми:

Теорема 1. Якщо функції танеперервні в точці, то в цій точці неперервні функції,,,.( остання – при додатковій умові, що).

Точки розриву функції, їх класифікація.

Означення. Функція називається розривною в точці, якщо не виконується хоча б одна з умов означення 1 неперервності функції.

В залежності від того, які умови неперервності виконуються чи не виконуються, будемо мати різні точки розриву.

1. Якщо виконується друга умова, а третя чи перша і третя не виконується, то точка називається точкою розриву першого роду ( звичайний розрив ).

2. Якщо в точці розриву не існує хоча б одна з односторонніх границь, то точка називається точкою розриву другого роду.

Якщо точка – точка розриву першого роду і в цій точці існує границя, то точканазивається точкою усувного розриву.

Так в розглянутому прикладі 4.1 функція в точцімає розрив другого роду, так як.