Задание 4

111. .112. .

113. .

4. Метод замены переменных

4.1. Замена.

Пусть дано некоторое тригонометрическое уравнение F(x) = 0. Обозначим через g(x) функцию и введем новое неизвестное. Если удастся выразить функцию F(x) через t, т. е. представить ее в виде, то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через.

Мы рассмотрим несколько случаев, когда это удается сделать.

Введем (в некотором тригонометрическом уравнении) новое неизвестное , тогда, применяя тождество

, находим

.

Ясно, что если уравнение содержит сумму функций и синус двойного угла, тогда его можно выразить через t.

Если левая часть тригонометрического уравнения F(x) = 0 может быть выражена через и, то целесообразно применить замену неизвестного по формулам,.

Пример 114. Решите уравнение .

Решение

Пусть , тогда , получим квадратное уравнение:

.

Получим совокупность уравнений:

.

Ответ: .

Замечание. Уравнение имеет решения в том и только в том случае, когда дискриминант уравнениянеотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию, так как.

Аналогично решаются уравнения вида .

Здесь удобно положить и тогда.

Пример 115. Решите уравнение .

Решение

1-й способ

Положим , тогда,, получим уравнение:

Ответ:

2-й способ

. Преобразуем уравнение, зная, что :

,

Дальнейшее решение такое же, как и в первом способе. Применяя второй способ, мы обходимся без введения новых переменных и без подстановки, но использовать его может лишь опытный человек, который имеет достаточно большой навык в решении тригонометрических уравнений, искусственных преобразованиях и т. п.

Пример 116. Решите уравнение .

Решение

Положим , тогда,, получим уравнение:

.

.

Ответ: .

Пример 117. Решите уравнение .

Решение

Пусть , тогда ,получим квадратное уравнение:

;

.

Ответ: ; .

Пример 118. Решите уравнение .

Решение

Положим , тогда,, получим уравнение:

- не удовлетворяет условию и является посторонним корнем.

.

Ответ: .

Пример 119. Решите уравнение .

Решение

Пусть , тогда ,получим уравнение:

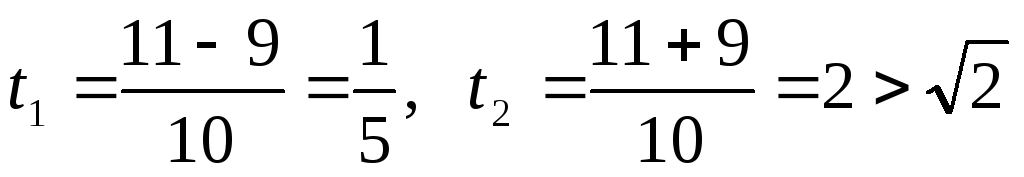- не удовлетворяет условию и является посторонним корнем.

,

.

Ответ: .

Пример 120. Решите уравнение.

Решение

Область допустимых значений:

Преобразуем уравнение:

.

Применим подстановку , тогда

, получим уравнение

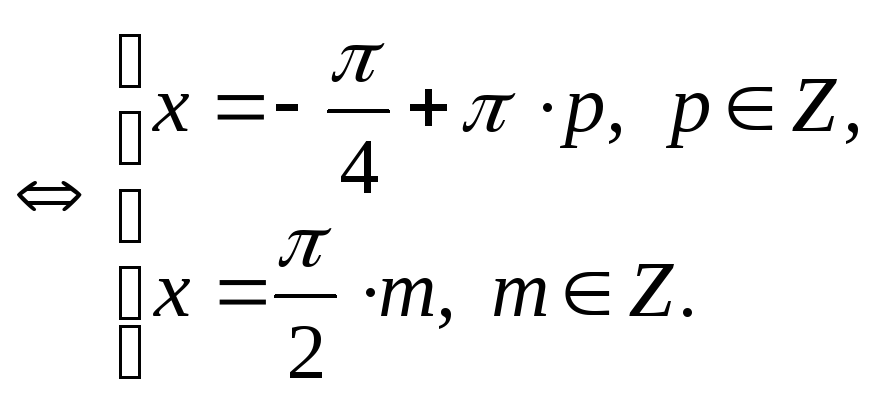
Определим, входят ли эти значения в область допустимых значений.

Проверим значения .

Оба неравенства выполняются при всех , значит- решения уравнения.

Проверим .

значит, m может принимать значения равные: m = 4n и m = 4n + 1, отсюда находим .

Ответ: .

Пример 121. Решите уравнение .

Решение

(Это один из способов решения. Другие будут приведены ниже).

Положим , тогда,, получим систему уравнений:

.

Ответ: .

Задание 5

122. .123. .

124. .125. .

126. .127. .

4.2. Замена

При такой замене через t легко выражаются и:

.

Если левая часть тригонометрического уравнения выражается через ,и, то можно выполнить замену переменных по формулам

причем .(1)

Рассмотрим, например, уравнение .

Это уравнение можно привести к однородному уже известным нам способом.

Однако проще его решить с помощью замены 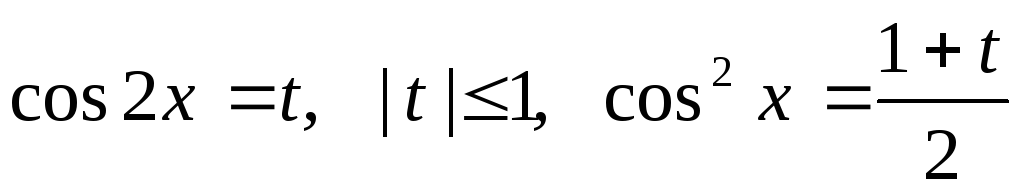, получим уравнение:.

Делая обратную подстановку, получим уравнение .

(К такому же результату можно придти заменив ).

Аналогично можно решать уравнения вида .

(В этом уравнении замена основана на формуле ).

Пример 128. Решите уравнение .

Решение

Преобразуем уравнение:

.

Выполним замену: , получим уравнение:

.

.

Ответ: .

Пример 129. Решите уравнение .

Решение

Преобразуем уравнение, используя формулы: , получим уравнение:

.

- эти корни не удовлетворяют условию и являются посторонними,.

Ответ: .

Пример 130. Решите уравнение .

Решение

Область допустимых значений: .

Выполним замену: , получим:

.

- не удовлетворяет условию и является посторонним корнем.

.

Определим значения x, которые входят в область допустимых значений.

Совокупность неравенств, каждое из которых выполняется при всех любых целых значениях , показывает, что все значенияx входят в область допустимых значений.

Ответ: .

Пример 131. Решите уравнение .

Решение

Выполним замену: , получим:

.

.

Ответ: .