Эконометрика (лабораторные)

получим преобразованную модель

yi

0

xi

i

,

(9.1)

i

i

1

i

i

для которой выполнены условия гомоскедастичности, так как

i

i

D(

i

)

2

М (

) 0,

D(

)

i

1 (i 1, n) .

i

i

i2

i2

Преобразованное уравнение представляет собой так называемую взвешенную регрессию с весом 1/ i . При минимизации суммы квадратов

y

i

b

x

i

2

1

2

0

b1

2 yi b0

b1 xi

слагаемые

отклонений Q

i

i

i

i

взвешиваются: наблюдениям с большей дисперсией придается меньший вес 1 / i2 и наоборот. Оценки МНК–коэффициентов преобразованной модели дают непосредственно оценки исходной модели.

Данный способ устранения гетероскедастичности применим, если известны фактические значения i, что практически не встречается на практике. Следовательно, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях i2 :

1) если i2 неизвестны,

их можно

заменять оценками si2 . Тогда

оценивается обычным МНК преобразованная модель

yi

0

xi

i

;

1

si

si

si

si

2) для экономических данных i

часто пропорциональны

значениям объясняющей переменной X (или X2):

пусть дисперсии i2 пропорциональны хi (рис.9.1 а): i2

2

xi

( 2 – коэффициент пропорциональности).

101

Рис.9.1.

Рассмотрим уравнение

yi

0

xi

i

=

0

v

.

(9.2)

1

1

x

i

i

xi

xi

xi

xi

xi

Оценив для (9.2) по МНК коэффициенты 0 и 1, затем возвращаются к исходному уравнению регрессии.

Если в уравнении регрессии присутствует несколько объясняющих переменных, можно поступить следующим образом. Вместо конкретной

объясняющей переменной Хj используется	ˆ	b0	b1 X1 ... bp X p
	Y

исходного уравнения множественной линейной регрессии, т.е. фактически линейная комбинация объясняющих переменных. В этом случае получают следующую регрессию:

y

i

1

xi

xip

i

.

1

0

1

p

yˆi

yˆi

yˆi

yˆi

yˆi

Иногда из всех объясняющих переменных выбирается наиболее подходящая, исходя из графического представления (рис.9.1);

	дисперсия i2		пропорциональна				xi2 (рис.9.1,б): i2	2	x 2i .
Тогда рассматривают модель						yi* 1 0 xi* i* ,			(9.3)
где y* y / x ,		x* 1/ x ,		*	i	/ x .
i	i i	i	i	i		i

В преобразованной модели выполняется условие гомоскедастичности. После определения МНК–оценок коэффициентов 0 и 1 для преобразованного уравнения возвращаются к исходному уравнению.

Задача 9.3. Оценить регрессионную зависимость выпуска продукции

102

перерабатывающей промышленности на душу населения Y от валового внутреннего продукта на душу населения X в том же году для 17 стран (данные условные):

X	3	6	7	9	13	15	18	21	22
Y	18	27	18	45	55	68	51	84	85
X	24	25	26	27	60	70	37	44
Y	100	63	130	136	28	35	80	180

Решение.

В файле «лаб9.xls» скопировать «Лист 2» (с помощью клавиш <Сtrl>+<Alt>+ левой кнопки мыши) и назвать его «Лист 3». В нем будем выполнять преобразования. Сначала очистите ячейки D3:F19. Далее, щелкнув по ячейке В4, три раза нажать ГЛАВНАЯ Вставить Вставить строки на лист. Аналогично добавить три новых строки, позиционируя курсор сначала в ячейке В9, затем в ячейке В15. Очистить диапазон ячеек В3:С19. Внести в очищенный диапазон исходные данные. При этом произойдет автоматический пересчет коэффициентов регрессии для первой и второй подвыборок.

Для проверки наличия гетероскедастичности применяется тест Голдфельда – Квандта.

Формулы-комментарии из ячеек G4 и G15 перетащить мышкой в ячейки G7 и G18. Аналогично формулы-комментарии для нахождения Fнабл

и Fкр перетащить мышкой напротив ячеек L7 и K18. В ячейках Н7 и Н18 вывести S1 и S3 , которые найдены с помощью функции ЛИНЕЙН. Для

этого в данные ячейки ввести соответственно формулы «=С25» и «=G25». В ячейках L7 и K18 получим, что Fнабл 43,69458 и Fкр =8,466125. Так как Fнабл >Fкр, то гипотеза об отсутствии гетероскедастичности отклоняется.

После установления гетероскедастичности модель необходимо пре– образовать с целью устранения этого недостатка.

Создадим шаблон для вывода исходного и преобразованного уравнений регрессии:

Для получения исходного уравнения регрессии, позиционируя курсор в ячейке В32, воспользоваться функцией ЛИНЕЙН, взяв в качестве известных значений у диапазон С3:С19, известных значений х – диапазон

103

В3:В19. Получено уравнение y 2,918489x 12,84377. Как было сказано, модель необходимо преобразовать. От уравнения y 0 1 x пере–

ходим к уравнению xy 0 1x 1 , где x , для которого выполняется

условие отсутствия гетероскедастичности. Для получения коэффициентов преобразованного уравнения проделаем следующее: в ячейках В35 и С35

введем заголовки столбцов t 1x и z xy . Далее в ячейке В36 введем фор–

мулу «=1/В3», в ячейку С31 – «=С3/В3». Выделив ячейки В36:С36, раз– множим формулу на диапазон В36:С52. Далее воспользуемся функцией ЛИНЕЙН, позиционируя курсор в ячейке G32, взяв в качестве известных значений у диапазон С36:С52, известных значений х – диапазон В36:В52.

	Получаем уравнение регрессии	y	7,782303	1	3,197809	или y=7,782303
		x		x

+3,197809 x. Для него выполняется условие гомоскедастичности.

9.3. Автокорреляция

В эконометрике различают два вида автокорреляции:

1)автокорреляция ошибок, или автокорреляция в отклонениях от регрессионной модели, которая появляется при нарушении одной из предпосылок Гаусса–Маркова;

2)автокорреляция в наблюдениях за одной или более переменными, которая будет рассмотрена в лабораторной работе № 10.

В случае наличия автокорреляции остатков полученная формула регрессии считается обычно неудовлетворительной. МНК–оценки в случае наличия автокорреляции первого порядка не смещены, состоятельны, но неэффективны. Оценка дисперсии при использовании МНК является заниженной, что может отрицательно сказаться на проверке гипотез о значимости коэффициентов регрессии. Образно говоря, МНК рисует более оптимистичную картину регрессии, чем есть на самом деле.

Одним из основных предполагаемых свойств отклонений i от

регрессионной модели является их статистическая независимость между собой. Поскольку значения i остаются неизвестными, то проверяется

статистическая независимость их аналогов – отклонений еi . При этом проверяется некоррелированность сдвинутыми на период величинами еi . Сдвиг производится во времени в случае временных рядов или по

104

возрастанию переменной в случае перекрестных выборок. Для этих величин можно рассчитать коэффициент автокорреляции первого порядка (выборочный коэффициент корреляции между еi и еi 1 ):

n

n

ei

ei 1

ei

ei 1

r

i 2

i 2

.

e

n

n 1

n 1

ei 2

ei 2

ei 2

i 1

i 1

i 1

На практике в качестве теста используют тесно связанную с

коэффициентом автокорреляции re статистику DW Дарбина–Уотсона:

n

2

(ei

ei 1 )

DW

i 2

2(1 r e).

n

ei

2

i 1

Пусть нулевая гипотеза H 0 состоит в отсутствии автокорреляции.

Тогда для решения

вопроса

о

принятии гипотезы H 0 можно

воспользоваться следующей таблицей:

Значение статистики DW	Вывод
4 dL DW 4	Гипотеза H 0 отвергается, есть
	отрицательная корреляция
4 dU DW 4 dL	Неопределенность
2 DW 4 dU	Принимается гипотеза H 0
dU DW 2	Принимается гипотеза H 0
dL DW dU	Неопределенность
0 DW dL	Гипотеза H 0 отвергается, есть
	положительная корреляция

Наличие зоны неопределенности, когда нет оснований ни принимать, ни отвергать гипотезу об отсутствии корреляции, представляет определенную трудность при использовании теста Дарбина–Уотсона. В грубом приближении можно сказать, что при числе наблюдений не меньше 12–15 и при 1–3 объясняющих переменных статистика DW должна быть не менее 1 и не более 3. В противном случае признается наличие авто– корреляции остатков и необходимо улучшить формулу. Если статистика DW находится между 1,2–1,3 и 2,7–2,8, можно сказать, что статистически значимая автокорреляция остатков отсутствует.

При наличии автокорреляции остатков можно искать другое уравнение регрессии, включить неучтенные до этого факторы либо

105

применить к данным уменьшающее автокорреляцию остатков преобразование (например, авторегрессионное преобразование или метод скользящих средних).

Задача 9.4. Определить наличие автокорреляции в задаче 8.1 лабораторной работы №8 с помощью критерия Дарбина–Уотсона.

Решение. Для проверки автокорреляции по критерию Дарбина– Уотсона воспользуемся данными лабораторной работы № 8. Откроем файл «лаб8.xls» и перейдем в нем на «Лист 2», который переименуем как «DW– критерий».

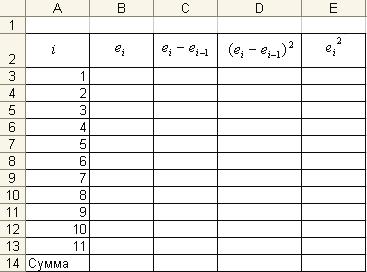
Далее сформируем таблицу как показано ниже:

Скопируем в ячейки В3:В13 значения остатков ei , находящиеся на

«Листе1» в диапазоне J74:J84. Для заполнения остальных столбцов вы– полним следующие действия. В ячейку С4 введем формулу «=В4–В3» и размножим ее на диапазон С4:С13. В ячейку D4 введем формулу «=С4^2» и размножим на диапазон D4:D13. В ячейку Е3 введем формулу «=В3^2» и размножим на диапазон Е3:Е13. В ячейках D14 и Е14 произведем суммирование вышестоящих элементов. Получим следующую таблицу

106

	Номер		ei yi	yˆi		ei ei 1		e	e	2			e 2
								i	i 1				i
	1		-2,0094									4,0377
	2		1,219135			3,228535		10,423438				1,48629
	3		0,079175			-1,13996		1,29951				0,006269
	4		-0,23251			-0,311685		0,097148				0,05406
	5		-0,42727			-0,19476		0,03793				0,18256
	6		0,548416			0,975686		0,951963				0,30076
	7		0,408456			-0,13996		0,01959				0,166836
	8		-0,52257			-0,931026		0,866809				0,27308
	9		0,850632			1,373202		1,885684				0,723575
	10		-3,00739			-3,858022		14,884334				9,04439
	11		3,093344			6,100734		37,218955				9,568777
	Сумма							67,685361				25,844297
													n
													(ei	ei 1 )2
В ячейке А17 введем формулу-комментарий										DW			i 2				, а в
													n
													ei		2
													i 2
ячейке D17 формулу для расчета «=D14/Е14». Получим значение
DW=2,6190. По таблице распределения Дарбина–Уотсона (приложение 1)
при 5%-м уровне значимости и n=11 находим dl												0,66		и du 1,60 .
Тогда 4 du		2,40,		4 dl		3,34 .	Так		как			4 du DW 4 dl

(2,40<2,6190<3,34), то гипотеза об отсутствии автокорреляции остатков не может быть ни принята, ни отвергнута.

9.4. Мультиколлинеарность

Под мультиколлинеарностью в моделях множественной линейной регрессии понимается линейная взаимосвязь двух или нескольких объясняющих переменных. В этом случае трудно разграничить их отдельное объясняющее взаимодействие на фактор Y. Тогда МНК, как метод оценки коэффициентов модели, не может быть использован.

Последствиями мультиколлинеарности являются:

107

большие дисперсии и стандартные ошибки S(bj ) оценок коэффициентов регрессии b0 , b1 , , bp , что расширяет доверительные

интервалы теоретических коэффициентов уравнения линейной регрессии;небольшие значения t–статистик оценок коэффициентов регрессии приводят к неверным выводам о статистической незначимости некоторых коэффициентов и о существенности влияния объясняющей переменной на зависимую переменную. При этом регрессионная модель может оказаться значимой по F–критерию, т.е. значение множественного коэффициента

корреляции завышено;небольшое изменение исходных данных и объема выборки приводит

к существенному изменению оценок параметров модели. Уравнение регрессии не имеет реального смысла, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории знаки и неоправданно большие значения;

затрудняется определение вклада каждой из объясняющих переменных в объясняемую уравнением линейной регрессии дисперсию результативного признака;

возможно получение неверного знака коэффициентов регрессии. Рассмотрение проблемы мультиколлинеарности начинается тогда,

когда это серьезно влияет на результаты оценки регрессии. Как правило, данная проблема является обычной для регрессии временных рядов. Если независимые переменные имеют ярко выраженный временной тренд, то они будут тесно коррелированы, и это может привести к мультиколлинеарности.

Хотя не существует точных количественных критериев для определения наличия мультиколлинеарности, тем не менее есть некоторые эвристические рекомендации по ее выявлению:

анализ матрицы парных линейных коэффициентов корреляции (вернее той ее части, которая относится к объясняющим переменным). Если в ней содержатся коэффициенты корреляции, по абсолютной величине превышающие значения 0,75–0,80, то это свидетельствует о присутствии мультиколлинеарности. В наибольшей степени ответственным за мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели, т.е. имеет более высокие по модулю значения коэффициентов парной линейной корреляции;

находят множественные коэффициенты детерминации между каждой из объясняющих переменных и другими. Чем ближе значение коэффициента множественной детерминации к единице, тем больше

108

ответственность за мультиколлинеарность фактора, выступающего в роли зависимой переменной. Сравнивая между собой коэффициенты множественной детерминации для различных факторов, можно проранжировать переменные по степеням ответственности за мультиколлинеарность;

существование тесных линейных статистических связей приводит к слабой невырожденности матрицы X T X . Если det X T X оказывается близким к нулю, то это также считается свидетельством мультиколлинеарности.

Для устранения или уменьшения мультиколлинеарности используется ряд методов:

изменение спецификации модели: либо изменяется форма модели, либо добавляются объясняющие переменные, не учтенные в первоначальной модели, но существенно влияющие на зависимую

переменную.
использование	пошаговых	процедур	отбора	наиболее

информативных переменных. На первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент детерминации. На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначально отобранной образует пару объясняющих переменных, имеющую с Y наиболее высокий (скорректированный) коэффициент детерминации. На третьем шаге вводится в регрессию еще одна объясняющая переменная, которая вместе с двумя первоначально отобранными образует тройку объясняющих переменных, имеющую с Y наибольший(скорректированный) коэффициент детерминации и т.д.

Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться соответствующий (скорректированный)

коэффициент детерминации.
простейшим	методом	устранения	или	уменьшения

мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных и др.

Задача 9.5. Имеются данные о заработной плате Y (усл. ед.), возрасте

X1 (лет),			стаже		работы		по специальности				X2	(лет),		выработке X 3
(шт./смену) по 20 рабочим:
	№	1		2		3	4	5	6		7		8		9	10
	Y	320		420		340	350	200	350		370		420		380	450
	X1	29		40		36	32	23	45		38		40		50	47

109

X 2	6	19	10	10	3	20	17	23	31	25
X 3	17	25	15	17	15	18	17	25	19	23
№	11	12	13	14	15	16	17	18	19	20
Y	250	320	220	400	220	340	400	380	260	250
X1	28	30	25	48	30	40	40	38	29	25
X 2	7	7	6	20	5	15	20	20	10	5
X 3	15	18	16	23	18	18	25	23	18	17

Требуется:

а) определить наличие мультиколлинеарности; б) построить регрессионную модель заработной платы.

Решение.

Перейдите на «Лист5» в файле «лаб9.xls». Внесите данные задачи по столбцам с соответствующими подписями в диапазон А2:Е22. В диапазоне А24:Е28 выведем описанным в предыдущих работах способом матрицу парных коэффициентов корреляции вместе с метками в первой строке:

	Y	X1	X2	X3
Y	1
X1	0,848213	1
X2	0,847941	0,935263	1
X3	0,761232	0,615448	0,696610	1

Так как r1,2 0,935263>0,8, то между признаками X1 и X2 имеет место

сильная корреляционная зависимость. Наличие мультиколлинеарности между факторами в трехфакторной модели отрицательно сказывается на качестве модели. Чтобы подтвердить это, построим регрессионную модель заработной платы, включив в нее все три факторных признака. Для нахождения параметров модели и дополнительной информации воспользуемся функцией ЛИНЕЙН. Применив данную функцию, выведем массив данных в диапазон А30:D34. В строке 36 создадим шаблон для вывода уравнения регрессии:

В ячейках В36, С36, Е36 и G36 для вывода коэффициентов регрессии введем соответственно формулы «=D30», «=С30», «=В30», «=А30».

110