Лекція 8 (продовження – 8.2)

Для визначення величини максимальних і мінімальних моментів інерції (головних моментів інерції) треба знайти значення кута через

arctg(.) і підставити у вихідний вираз для осьових моментів інерції, або безпосередньо використовувати тригонометричні формули

подвійних кутів, як це було зроблено, наприклад, при визначенні головних напружень. Тут зробимо трохи інакше.

Представимо осьовий момент у вигляді:

I x

I y

I x I y

I x I y

I x I y

Iu

1

.

Iu I x cos2 I y sin2 I xy sin 2 .

Iu

cos 2

I xy

sin 2

2

2

cos 2

2

2

2I xy

cos2 1 cos 2

tg2

.

2

I x I y

sin 2 1 cos 2

I x I y

sin 2

1 tg 2 2

2

2I xy

2

cos 2

tg2

.

I x

I y

Підставляючи останній вираз і скорочуючи

I x I y

Iu

1

I x I y 2 4I xy2 .

різницю моментів інерції отримуємо остаточно:

2

2

1

2

2

(I x I y )

4I xy

I x I y

Знак плюс перед другим доданком відноситься до максимального моменту, знак мінус - до мінімального.

Зауваження. Отримані формули для моментів інерції, пов'язані з поворотом осей, а також для головних моментів інерції, практично аналогічні по структурі відповідних формул для нормальних і дотичних напружень на похилих майданчиках і для головних

напружень. Звідси можна зробити висновок, що положення осей, відповідних екстремальним значенням моментів інерції і самі значення можна знаходити за допомогою кола Мора, побудованого для моментів інерції.

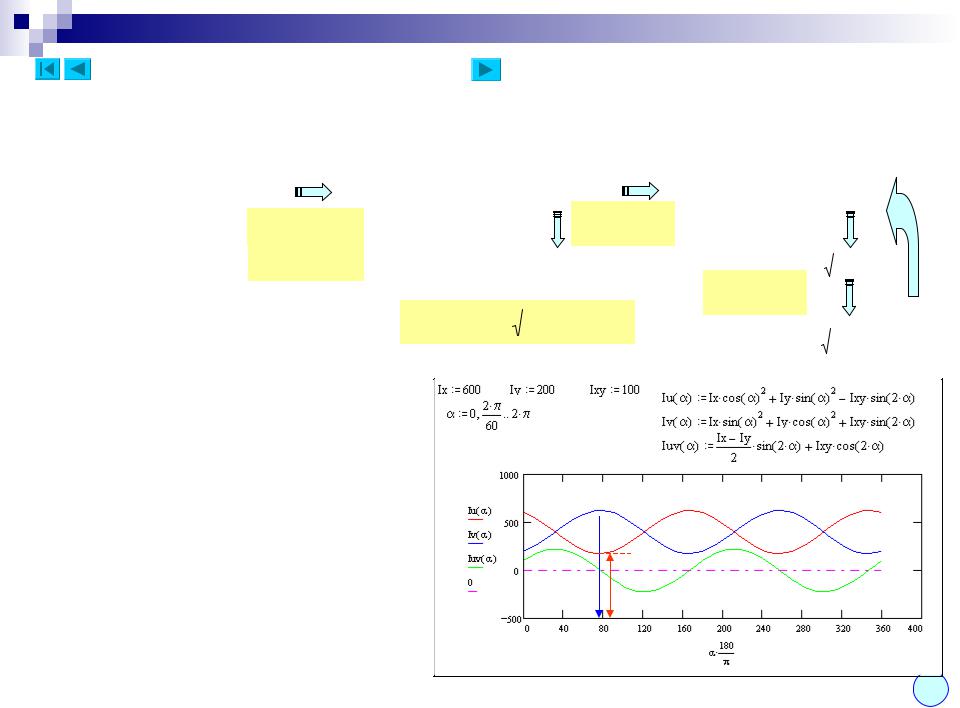
Тут же проілюструємо характер зміни моментів інерції при послідовному повороті осей в діапазоні 0 – 2 π (графіки побудовані в системі MathCAD):

Добре видно, що при досягненні осьовими моментами інерції максимальних і мінімальних значень відцентровий момент інерції обертається в нуль.

А при досягненні відцентровим моментом інерції максимального значення (при повороті від головних осей на 45 о ) осьові моменти стають рівними між собою.

Iu Iv

Imax

Imin

Iuv

28

Лекція 8 (продовження – 8.3)

Радіус інерції - є величина, що зв'язує момент інерції з площею поперечного перерізу і визначається з рівності:

Радіус інерції являє собою відстань від розглянутої осі до тієї точки, в якій умовно можна зосередити

всю площу поперечного перерізу. Ця величина характеризує наскільки добре "розвинений" переріз, як далеко знаходяться від осі

окремі області перерізу, що в свою чергу характеризує економічність перерізу при згині і стиску із згином.

Радіусом інерції зручно користуватися при оцінці гнучкості стиснутих стержнів.

ix

I x .

Звичайно для цього радіуси інерції попередньо обчислюються для типових і прокатних перерізів за формулами:

Imax

Imin

A

Радіуси інерції, відповідні головним осях, називаються

imax

.

imin

.

головними радіусами інерції і визначаються за формулами:

A

A

Обчислення моментів інерції складних фігур - виконується в наступному порядку:

Переріз розбивається на частини, для яких відомі координати центрів ваги і моменти інерції або легко знаходяться.

Вибираються початкові осі, щодо яких обчислюються координати центру ваги перерізу.

Обчислюються координати центра ваги перерізу.

Проводяться центральні осі (що проходять через центр ваги перерізу), щодо яких обчислюються моменти інерції.

Обчислюються осьові і відцентрові моменти інерції всього перерізу щодо центральних осей.

Обчислюються головні центральні моменти і визначається положення головних осей.

a1 y1

yc

Приклад 1 - Визначити головні

x t

,

y

h ,

A h t

xc x1

A1

x2 A2

центральні моменти інерції

1

1

t2

1

A A

a2 y2

yc

і положення головних осей

a t2

A2 a

t t

y1 A11

y22

A2 ;

b x

x

c

кутикового поперечного перерізу.

x2 2

,

y2 2 ,

yc

A1 A2

1

1

b x

2

x

c

Ix

t h3

A1 a12 a t t3

2

Ix

ВЛ

A a2

A2 a22 ,

t 2

yC

C

12

12

I y

y

1

I y

ВЛ

A b2

h t3

A1 b12 t a t 3

A2 b22 ,

1

C

12

12

h

C

2

xC

IxyC

IxyВЛ A a b 0 A1 a1 b1 0 A2 a2 b2 .

O

t

x

2I

I

I

cos2 I

sin 2 I

sin 2 .

xy

u

x

y

xy

x1

x2

tg2

.

I x

I y

Iu

I x sin 2 I y cos2 I xy sin 2 .

a

I x ix2 A.

Iy iy2 A.

iy IAy .

29

Лекція 9 Тема: ДОСЛІДЖЕННЯ НАПРУЖЕНОГО СТАНУ ТІЛА В ТОЧЦІ

1.Загальні відомості про напружений і деформований стани в точці. Тензор напружень.

2.Закон парності дотичних напружень.

3.Напруження на похилих площадках.

4.Головні нормальні напруження та максимальні дотичні напруження.

5.Головні деформації.

Основні гіпотези:

у	σy
	yx
σx xy		σx
		xy
	yx	x
	σy

1.Гіпотеза про суцільність матеріалу. Передбачається, що матеріал суцільно заповнює форму тіла (атомістична теорія дискретної побудови речовини до уваги не береться).

2.Гіпотеза про однорідність та ізотропність. Передбачається, що властивості матеріалу по всьому його об’ємі і в любому напрямку

будуть однакові, тобто ізотропні.

3.Гіпотеза про незначні деформації. Передбачається, що деформації в тілі досить малі порівняно з його розмірами.

4.Гіпотеза про ідеальну пружність матеріалу. Передбачається, що під дією навантаження в тілі виникають пружні деформації, тобто

такі, що повністю зникають після зняття навантаження.

5. Гіпотеза про прямопропорційну залежність між навантаженням і деформаціями. Закон Гука: “Яка сила, така й деформація”.

	Зовнішні сили		M
			B
зосереджені або розподілені	постійні або тимчасові	статичні або динамічні	VB

поздовжня сила

нормальні

σ

ε

	Внутрішні зусилля			y	My		M
	поперечна сила		згинаючий момент крутний момент
				Mz Nσz	x	zy
	Напруження – інтенсивність внутрішніх зусиль;
				Qу
	– внутрішнє зусилля, що діє на одиницю площі в даній точці. z			O		Q	zx
σ	дотичні					x
			Деформації – зміна розмірів тіла:				Mx
		γ					x
			ε – поздовжніх,
			γ – кутових.

F

F

30

1	Лекція 9 (продовження – 9.2)
	Розглянемо довільне тіло, завантажене будь-яким навантаженням.

F F F

	Рz	y
		Рzу = τzу
	z
	Рzх = σz	Рzх = τzх
		x

Внаслідок взаємодії частинок тіла при його навантаженні, у перерізах тіла виникають напруження.

Досліджуючи напружений стан тіла в даній точці А, поблизу неї, як правило, виділяють елемент об’єму

у вигляді нескінченно малого паралелепіпеда.

Ру

σy

Покажемоyzвирізаний паралелепіпед у збільшеному вигляді.

y

zy

yx

До граней паралелепіпеда прикладені внутрішні зусилля, що замінюють

дію відкинутої частини тіла. Позначимо повні напруження на гранях

σ

xy

елемента через Рх, Ру і Рz. Тут індекси означають нормалі до площадок,

Рz z

на яких діють напруження. Внаслідок малості виділеного елемента

z

zx xz

σx

можна вважати, що напруження на кожній його грані розподілені

рівномірно.

x

Рх

Повні напруження на гранях елемента розкладають на нормальні та

дотичні до граней складові – проекції повних напружень на координатні

осі. Індекс біля нормальних напружень σ відповідає напряму нормалі до

σy

площадки, на якій вони діють. Дотичні напруження τ позначають з

yz

двома індексами: перший відповідає напряму нормалі до площини, а

y zy

yx

другий – напряму самого напруження.

Таким чином, на площадці, перпендикулярній до осі х діють напруження

σ

xy

σх, τху і τхz.

z

z

На площадці, перпендикулярній до осі у діють напруження σy, τуx і τyz.

zx xz

σx

На площадці, перпендикулярній до осі z діють напруження σz, τzx і τzy.

x

Отже, на гранях елементарного паралелепіпеда, виділеного в околі точки А навантаженого тіла, діють дев’ять компонент напружень. Запишемо їх у вигляді квадратної матриці, де в першому, другому та

третьому рядках наведено складові напружень відповідно на площадках, перпендикулярних до осей x, y, z. Цю сукупність напружень називають тензором напружень.

Px →		σх τху τхz
Py →		τyx σy τyz	= T
Pz →		τzх τzy σх

Вирізаний нами елемент (паралелепіпед) можна по різному орієнтувати у просторі. При поворотах елементу нормальні та дотичні напруження на його похилих гранях будуть приймати нові значення. Тому необхідно дослідити, як змінюються ці напруження від орієнтації елементу. Розглянувши це питання, можна знайти похилі площадки, на яких напруження приймають максимальні та нульові

значення.

Розглянемо цю задачу спочатку для більш простого випадку – плоского напруженого стану.

31

2 Лекція 9 (продовження – 9.3)

Плоский напружений стан – такий стан, при якому дві паралельні грані елементу вільні від напружень,

yz

σy

тобто на них відсутні і нормальні, і дотичні напруження. Такий стан виникає в тонких пластинках, поверхні яких

y zy

σx

yx

вільні від навантаження, на ненавантаженій поверхні тіл, при згині балок, крученні валів тощо.

σ

xy

z

xy

z

Розглянемо нескінченно малий об’єм у вигляді паралелепіпеда навколо досліджуваної точки А.

zx

xz

σx

yx

σ

y

Нехай, наприклад, по площадці, перпендикулярній вісі z

Нижче буде показано, що в цьому випадку

x

напруження zx і

zу також будуть відсутні.

напруження відсутні.

Тепер об’ємний елемент можна представити у вигляді його проекції на площину ху.

у

yx

σy

На рисунку показані додатні напрямки напружень, що відповідають наступним правилам:

xy

1. додатні нормальні напруження направлені в сторону зовнішньої нормалі відповідної грані, тобто вони

викликають деформації розтягу елементу;

σx

σx

2. додатні дотичні напруження повертають елемент по годинниковій стрілці (назустріч осі z).

dy

xy

У загальному випадку, напруження в деформованому стані змінюються від точки до точки, тобто являються

dx

функціями координат. Тут при розгляді нескінченно малого елементу можна вважати, що напружений стан

A

однорідний і напруження по кожній грані постійні і на паралельних гранях елементу рівні між собою.

yx

x

Виділений елемент повинен знаходиться у рівновазі та задовольняти рівнянням рівноваги для будь-якої плоскої

σy

системи сил – рівнодіючої по кожній із граней прикладених зусиль:

- суми проекцій на координатні осі тотожно рівні нулю.

Складемо суму моментів всіх сил відносно лівого нижнього кута (точки А):

M Ai 0;

- ( yxdxdz)dy ( xydydz)dx 0.

yx xy

Отриманий закон парності дотичних напружень: Дотичні напруження на двох взаємно перпендикулярних площадках

рівні один одному по величині та протилежні по знаку.

Таким чином, показані напрямки дотичних напружень на рисунку, присвячених правилам знаків, не відповідають стану рівноваги елементу. Можливі правильні напрямки дотичних напружень будуть наступні:

yx<0

yx>0

xy

xy<0

xy>0

xy

yx

yx

32

3

Лекція 10

Напруження на похилих площадках.

Для визначення напружень на похилій площадці, зовнішня нормаль якої повернута

на кут α до осі х, використовуємо метод перерізів:

σy

у

dy

cos

1. проведемо похилий переріз;

y

yx

2. відкинемо праву частину;

n

xy

σx

3. замінимо відкинуту частину внутрішніми зусиллями, які представимо у

dy

σ

вигляді компонент напружень – нормального та дотичного (на рисунку всі

z

σx

напруження показані додатними);

t

4. складемо рівняння рівноваги для рівнодіючих напружень в проекціях на

yx

x

нормаль n до похилого перерізу та вісь, дотичну t до перерізу:

x dz

σy

dy

(n) :

dz

dy.tg

x (dydz) cos y ((dy tg )dz)sin yx (dy tg dz) cos xy (dydz)sin 0,

cos

(t) :

dy

x (dydz)sin y ((dy tg )dz) coss yx (dy tg dz)sin xy (dydz) cos 0.

dz

cos

Після ділення рівнянь на dydz, множення на cos , підстановки закону парності дотичних напружень та переносу у праву частину відомих

напружень, отримаємо:

x cos2 y sin2 yx sin 2 ,

x cos2 y sin2 2 yx sin cos ,

Або використовуючи

x sin cos y sin cos yx (sin2 cos2 ).

відомі тригонометричні

x

y

формули подвійного кута:

sin 2 yx cos 2

Отримані формули для визначення напружень на будь-яких площадках, що проходять через дану

2

точку, якщо відомі напруження x, y і yx = - xy.

Визначимо, які будуть напруження на площадці, перпендикулярній до розглядуваної похилої

площадки:

900 x cos

2

( 90

0

) y sin

2

( 90

0

) yx sin 2( 90

0

) x sin

2

y cos

2

yx sin 2 .

x

y sin 2( 900 )

cos 2( 900 )

x

y

sin 2

cos 2

90

0

2

yx

2

yx

Із порівняння виразів для дотичних напружень знову можна отримати закон парності дотичних напружень:

Додаючи вирази для нормальних напружень, отримуємо закон незмінності суми нормальних напружень на будь-яких взаємно-перпендикулярних площадках:

Із незмінності суми нормальних напружень слідує, що при повороті цих площадок приріст					900 .
(зміна) нормальних напружень однакові і протилежні за знаком:	d d	900	0;	d - d

Відповідно, якщо на одній із площадок нормальні напруження досягають максимуму, то на другій площадці вони перетворюються в мінімальні.

+900 = - .

900 x y const.

33

4 Лекція 10 (продовження – 10.2)

Головні напруження. При розрахунку конструкцій на міцність необхідно визначати величину максимальних напружень. Максимальні та мінімальні нормальні напруження називаються головними напруженнями, а площадки, на яких вони діють – головними площадками.

Для визначення положення головних площадок достатньо прирівняти до нуля першу похідну нормальних напружень по куту нахилу площадок:

x cos		2	y sin			2		yx sin 2			x ( 2cos )sin y 2sin cos yx 2cos 2 ( x y )sin 2 2 yx cos 2 0.
	tg2			2 yx	.			Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз
								визначає дві площадки, що відрізняються один від одного на 900. Таким чином, обидві головні площадки взаємно
				x y				перпендикулярні.

	Зауважимо, що похідна нормальних напружень на похилій площадці по куту нахилу		( x y )sin 2 2 yx cos 2 2 .
	площадки рівна подвоєній величині дотичних напружень на цій площадці. Таким чином,
	на головних площадках дотичні напруження дорівнюють нулю.

Для визначення величини максимальних і мінімальних нормальних напружень необхідно знайти значення кута через arctg(…) і підставити у вихідний вираз для нормальних напружень. Але простіше безпосередньо використати наступні тригонометричні формули:

									2 yx
sin 2			tg2				x y												2 yx								cos 2	1									1									x		y
		1 tg2 2							2	yx		2					( x y )2			4 yx2								1 tg2 2									2	yx	2					( x y )2 4 yx2
				1																													1
									x y																		x y										x y												x y
														cos		2		1 cos 2						1									sin		2		1 cos 2								1
																			2					2															2						2
																										2
																											( x y )2 4 yx2																				2		( x y )2 4 yx2

Підстановка цих тригонометричних функцій у формулу нормальних напружень дає для однієї із головних площадок:

		1								x y									1					x y
x			2														y		2												yx
							2 ( x y )				2		2								2 ( x y )					2		2
													4 yx														4 yx
	x y							( x y )2 4 2yx									x y						1
																									( x y )2			4 yx2 .
	2							2 ( x y )				2	2						2				2
													4 yx

2 yx

Оскільки кут для другої головної площадки

0

відрізняється від першої на 90 , то синус і косинус

( x y )2

4 yx2

подвійного кута змінює знак на протилежний, що

приводить до зміни знаку другого доданку:

x y

1

2

2

( x y )

4 yx .

2

2

Таким чином, по двом головним площадкам		x y		1							x y		1
						2	2								2	2
діють головні напруження:	max				( x y )		4 yx .			min				( x y )		4 yx .
		2		2							2		2					34

Лекція 10 (продовження – 10.3)

	Максимальні дотичні напруження. Існують площадки, на яких дотичні напруження досягають максимальних значень. Для визначення
	їх положення достатньо прирівняти до нуля першу похідну дотичних напружень по куту нахилу площадок:

x

y

x y

x y

sin 2 yx cos 2

2cos 2 yx 2sin 2 ( x

y ) cos 2 2 yx sin 2 0.

tg2 1

.

2 yx

2

2

Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає дві площадки, що

відрізняються одна від одного на 900. Таким чином, обидві площадки взаємно перпендикулярні. Проте на цих площадках у загальному

випадку нормальні напруження перетворюються в нуль.

Площадки, на яких дотичні напруження максимальні, називаються площадками зсуву.

tg2

2 yx

.

Визначимо кут між площадкою зсуву і головною площадкою.

Порівняємо формули для кутів нахилу головних площадок та площадок зсуву:

x

y

Оскільки праві частини

1

tg2 1

.

ctg(900

2 1 ) ctg2 .

900

2 1

2 .

1 450.

обернені один одному, то

tg2

Таким чином, площадки зсуву повернуті відносно головних площадок на кут 450.

Для визначення величини максимальних дотичних напружень необхідно знайти значення кута через arctg(…) і підставити у вихідний вираз для

дотичних напружень, але простіше прийняти у якості вихідного стану головні площадки і перейти до площадок зсуву:

x y

sin 2 yx cos 2

max

min sin(2 450 )

0 cos(2

450 )

max

min .

2

2

2

При підстановці кута 135

0

або -45

0

(друга площадка зсуву) отримаємо той же результат, але із оберненим знаком.

max

min .

max,min

Таким чином, знову дотримується закон парності дотичних напружень і в загальному випадку можна записати:

2

Підставимо вирази для

x

y

1

x

y

1

1

2

2

2

2

2

2

головних напружень:

max

( x y )

4 yx .

min

( x y )

4 yx .

max,min

( x

y )

4 yx .

5

2

2

2

2

2

Поняття про круг Мора для напружень.

Існує графічний спосіб визначення положень головних площадок та напружень, а також напружень на будь-яких інших площадках. Спосіб

базується на залежності між нормальними і дотичними напруженнями, що описується рівнянням ІІ порядку, а саме рівнянням круга.

1 cos y

1 cos

x

y

x

y

cos 2 yx sin 2

Отже, отримане рівняння ІІ порядку:

x

yx sin 2

2

2

x y

2

2

x

y

2

2

2

2 2

2

yx .

квадрату

x

y

2

x

y

(cos2 2 sin 2

2 )

2

(sin 2 2 cos2

2 )

yx

2

2

рівнянь

2

2

= 1

= 1

= 0

і

x y

Порівняємо його з рівнянням круга:

35

2

yx

(sin 2 cos 2 sin 2 cos 2 )

.

(x a)2

( y b)2

R2 .

2

Лекція 10 (продовження – 10.4)

Побудова круга Мора і його використання. Із порівнянь рівнянь координати

Рівняння зв’язку нормальних і дотичних

центр круга Мора і радіус рівні:

напружень:

2

2 .

2

2

Побудуємо круг Мора для

a x

y

, b 0, R

x

y

2

2 .

2

2

yx

x

y

x

y

напруженого стану:

2

2

yx

σy

x

y

Рівняння круга:

у

yx

a

2

(x a)

2

( y b)

2

R

2

.

M

σx xy

σx

B

max

2

Точка перетину напрямків площадок із

R

x y

2

колом (точка С) називається полюсом для

yx

даного вихідного стану, і визначає напрямок

xy

2

yx

будь-якої похилої площадки, напружений

yx

O

σ

x

стан якої позначається точкою круга Мора,

σ

σ

σmin

xy

наприклад, точкою М:

y

min

Напружений стан на площадці х

σy

С

A

Підрахуємо тангенс кута нахилу площадки,

що відповідає точці М, до площадки х:

характеризується точкою А на кругі

σmax

(( x

y ) cos

2 yx sin )sin

напружень.

tg

tg

Напружений стан на площадці у

σx

((

x

y

) cos

2

yx

sin ) cos

характеризується точкою В на кругі

напружень.

x y

Таким чином, пряма СМ, що

xy 0

2sin cos

2sin 2

з’єднує показану точку М із

sin 2 xy cos 2

xy

x

y

xy

2

sin 2 yx (cos 2 1)

полюсом С, показує напрямок

tg

2

y

( x

cos 2 y sin 2 xy sin 2 ) y

tg

похилої площадки, по якій

2

y (sin

2

1) yx sin 2 )

діють напруження σ , .

yx

xy

x cos

cos2

2sin cos

x cos2 y sin2 yx sin 2 ,

За допомогою круга Мора легко визначаються головні напруження і

напрямок головних площадок,

x

y sin 2 yx cos 2

екстремальні дотичні напруження і напрямок площадок зсуву.

2

yx xy

36

6

Лекція 10 (продовження – 10.5)

Головні деформації.

Аналогічно визначенню напружень на похилих площадках, можуть бути визначені деформації. Вирази деформацій в новій системі

координат, повернутій відносно початкової на деякий кут, аналогічні виразам для напружень. Достатньо підставити замість нормальних

напружень лінійні деформації, а замість дотичних напружень – половини кутів зсуву:

x

cos2

y

sin 2 1

yx

sin 2 ,

x y

sin 2

1

yx

cos 2 .

2

2

2

Також, як і для напружень, існують такі площадки, для яких відсутні кути зсуву, а лінійні деформації приймають максимальні значення. Ці площадки і лінійні деформації називаються головними. Для їх визначення використовують формули, аналогічні отриманим для напружень:

	x y		1							yx
					2	2			tg2		.
max				( x y )		yx .
										x y
	2		2

За допомогою круга Мора, побудованого для деформацій, легко визначаються головні деформації та напрямок головних площадок.

37