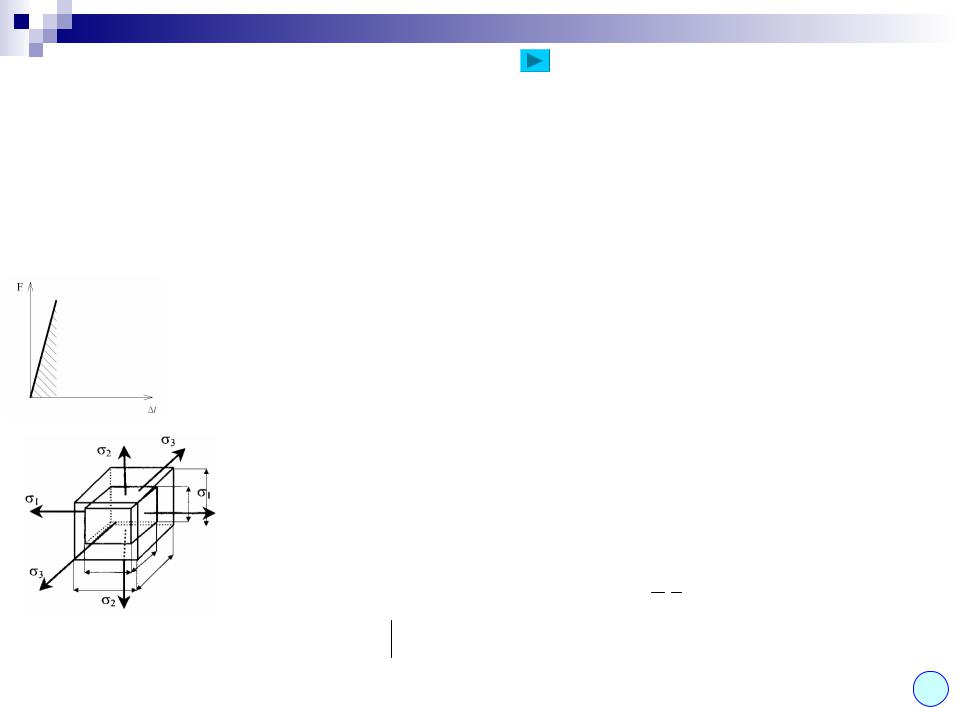
Лекція 11

Деформації при об’ємному напруженому стані. Узагальнений закон Гука.

При лінійному напруженому стані:

l		– відносна поздовжня деформація;
	a l a	a			b b						b
	a	a	або			b					b	– відносна поперечна деформація.
Закон Гука в загальному вигляді							E
																	E
Коефіцієнт
Пуассона
																					E
При об’ємному напруженому стані:																		a відповідно повна деформація тіла буде виглядати так:
																									1
																							1											2			3
											напруження														E			1
			деформації
																									1
							1							2				3					2						2						3			1
																									E
				1																3					1
							1								2
						E									E				E				3						3						1		2
																									E
				2					1					2						3
													E						E
								E

3

3

1

2

E

d

dy

d

E

E

1

x

; 2

; 3

z

.

dx

dy

dz

Згідно з принципом

незалежності дії сил,

запишемо

1

1

2

3

повні деформації у напрямку дії напруження σ1:

E

E

E

Це і є узагальнений закон Гука, в напруженнях, який дозволяє встановити взаємозв'язок між лінійними деформаціями і головними нормальними напруженнями. Цей закон Гука справедливий не тільки для головних площадок, але і для відносних деформацій по будь-якому із трьох взаємно перпендикулярних напрямків.

38

Лекція 11 (продовження – 11.2)

Об’ємна деформація. Об’ємний закон Гука.

Узагальнений закон Гука дає можливість оцінити відносну зміну об'єму. Так, до деформування елемент займав об'єм V0 dx d y

dz

У деформованому стані: V

d

x

d

x

y

d

y

z

z

d

d

d

Перемножимо дужки, нехтуючи величинами другого та третього порядку малості:

V

d

x

d

x

y

d

y

z

z

x

y

x

y

x

y

x

y

d

d

d

d

d

d

d

d

d

d

d

d

z

d

z

d

x

d

y

d

d

d d

d d

y

d

z

d d

y

d

z

x

y

z

x

x

z

d

x

d

y

d

d

x

d

d

d d

d d d d

z

z

y

z

x

y

z

x

y

d

x

d

y

d

z

d

x

d d

d d d

z

d

x

d

y

d

z

y

z

x

y

dx

d y

dz

V V

V

V

d

d

0

0

d

x

y

z

0

0

1

2

3

V

V

V V V V V

V V

Тоді

v

0

1

2

3

1

2 3

0

0

0

1

2

3

0

0

1

2

3

V0

V0

Таким чином

v

1

2

3

- відносна зміна об’єму

Підставляємо деформації із узагальненого закону Гука в відносну зміну об’єму:

v

1

2

3

1

1

1

E

1

2

3

E

2

1

3

E

3

1

2

1

E

1

2

3

2

1

3

3

1

2

1

1

2

3

1

2

3

1 2

1

2

3

E

2

E

Із цього співвідношення видно, що відносна зміна об'єму дорівнює нулю в двох

1 2

випадках:

v

1

2

3

- об’ємний закон Гука.

2

0

E

1) коли коефіцієнт Пуассона ν=0,5

(гума);

, а

2) при чистому зсуві, для якого

max

min

p

При рівномірному всебічному

1

2

3 p

v

K

стиску, коли:

K

E

називається модулем об'ємної деформації матеріалу. 39

де

3

1 2

Лекція 11 (продовження – 11.3)

Потенціальна енергія деформації.

Потенціальною енергією деформації називається енергія, що накопичується в тілі під час його пружному деформуванні. Коли під дією зовнішнього статичного навантаження тіло деформується, точки прикладення зовнішніх сил переміщуються, і потенціальна енергія положення навантаження зменшується на величину, яка кількісно дорівнює роботі, здійсненій зовнішніми силами. Енергія, втрачена зовнішніми силами, не

зникає, а перетворюється, в основному, на потенціальну енергію деформації тіла.

Потенціальна енергія деформації U накопичується в оборотній формі – в процесі розвантаження тіла знову перетворюється на енергію

зовнішніх сил або на кінетичну енергію. Значення потенціальної енергії деформації, яка припадає на одиницю об’єму тіла, називається

питомою потенціальною енергією деформації (и).

При розтязі чи стиску потенціальну енергію деформації можна визначити по площі діаграми після побудови діаграми деформації матеріалу на ділянці пропорційності.

	При лінійному напруженому стані:																																										F									l											F l
												F l																					Так як												та										маємо u																				.
								U						- потенціальна енергія деформації.
																																											A										l										2 A l									2
												2
																															F l
								Використовуючи розгорнутий закон Гука: l																								,	Використовуючи закон Гука: E																																										,	u						2				- питома
																															E A
												F l				F 2 l																																																									E					2 E				2 E
								U													- повна енергія деформації.												потенціальна енергія при одноосному розтязі чи стиску стержнів.
												2			2 E A
								u			F l			- питома потенціальна енергія деформації.																			По аналогії: U																2				- питома потенціальна енергія при зсуві.
										2 A l
																																																2 G
														При об’ємному напруженому стані. Для																			Оскільки площі граней дорівнюють одиниці, то зусилля, що діють
														цього					виріжемо					елемент				у	вигляді				на них, чисельно дорівнюють . Ці зусилля здійснюють роботу на
																																	тих переміщеннях, які дістають грані внаслідок деформації кубика.
														кубика							з		довжинами					ребер,			що
																																	Ці переміщення чисельно дорівнюють головним відносним
														дорівнюють									одиниці,		грані				якого є				видовженням , оскільки ребра мають одиничну величину. Отже,
																																	можна записати:
														головними									площадками.					На		цих
																																	u 1 1									2		2			3 3
														площадках									діють	головні				напруження															2
																																				2													2
															1	,	2	,			3	.																1			1						2			3							1				2					1				3						1		3			1		2
																																			1																			2																				3
																																		2			E																	2				E																2		E
																																			1
																																									2																			2																		2
			1 2			2		2																																																																																3
																																		2 E						1						1			2					1			2			2					1			2						2		3		3		2	3						1
	u					2		3	2
		2
			E 1											1		2			2				3	3 1										1							2			2		2			2
																																								1																1
								– загальна питома потенціальна енергія																										2 E									2				3										2					2 3					1				3
																																																																																								40
								деформації при об'ємному напруженому стані.

Лекція 11 (продовження – 11.4)

Питома потенціальна енергія формозміни.

При деформуванні елемента взагалі змінюється як його об’єм, так і форма: и = иv + иф.

Безпосередньо визначити иф важко, тому знайдемо спочатку енергію зміни об’єму иv . Це можна зробити, виходячи з припущення про те, що в різних елементах при дії різних головних напружень значення иv буде однакове, якщо елементи будуть однаково змінювати об’єми εv.

Крім розглядуваного елементу (назвемо його А) введемо ще допоміжний елемент А΄. Нехай А΄ – також одиничний кубик, але по його гранях
діють однакові головні напруження									1 2 3 . Тоді для цього елементу:															3 2	1 2
	1 2					3 1 2			u				1	2	2	2	2
											uV	uф		1	2	3		1	2	2	3	3	1
V		E	1 2	3		E							2 E												2 E

Проте очевидно, що елемент А΄ при деформуванні, спричиненими

однаковими по гранях напруженнями, змінюватиме тільки свій об’єм, а його

	форма залишиться кубічною. Тому uф 0														і uV	3	2	1 2			.
																		2 E
			Виберемо величину такою, щоб V V , тобто щоб
			1 2			1 2 3						3 1 2					Тоді				1 2	3	.
			E									E		.							3
			Оскільки в обох елементах зміни об’ємів однакові на підставі прийнятого
	припущення, то можна стверджувати, що
	u	u		3 2			1 2		3 1 2				1 2			3	2
																	, тобто
	V		V				2 E					2 E			3
	uv		1 2		1 2 3 2							- питома потенціальна енергія деформування,
			6E									що йде на зміну об’єму.

				Тоді
	uф u uV					1				12					22 32 2 1 2 2 3 3 1
						2 E
			1 2																	1
					1 2 3 2																	12				22 32 2 1 2 2 3 3 1
			6 E															2 E
			1 2		12 1 2 1 3 22 1 2 2 3 32 1 3 2 3
			6 E
									1												3 3 1																		1 2 2 3 3
			12	22	32												2 2													12			22 32
				2 E																E													6 E										3 E
			12 22			32								2 1 2 2 3 3 1																						12			22 32
																																	1
				3 E																		3 E																		3 E
																								1					12 22 32 1 2 2 3 3 1
	1 1							2					2			3			3			1			3	E
												3 E
			u u u									1							2					2				2
													3E											2				3			1			2		2		3			3		1
			ф				v												1

– питома потенціальна енергія, що витрачається на зміну форми елемента, що деформується.

41

Лекція 11 (продовження – 11.5)

42

Лекція 11 (продовження – 11.6)

43

Лекція 12

■ Загальні поняття про теорії міцності - При випробуваннях матеріалів статичним навантаженням на центральне розтягування (стиснення) досягається граничний стан, що характеризується настанням текучості, появою значних залишкових деформацій і / або тріщин. Для пластичних матеріалів за граничну або небезпечну величину напружень приймається межа текучості Т, для крихких - межа міцності В.

При експлуатації конструкцій в загальному випадку по площадках елементарного об’єму виникають нормальні і дотичні напруження,. пропорційні збільшенню навантаження. Значення кожного з напружень залежать від орієнтації розглянутих площадок.

yz	σy
y zy	yx
σz	xy

zzx xz σx

x

σ3

σ2

σ2

σ1

σ3

σz

Варіацією кутів повороту площадок можна визначити площадки, вільні від дотичних напружень, на яких виникають максимальні нормальні напруження. Такі площадки і напруження називаються головними (способи їх визначення для

плоского напруженого стану були розглянуті на лекції 9 даного курсу).

Саме головні напруження і можуть служити об'єктивною характеристикою напруженого стану в точці, оскільки вони є

інваріантами - величинами, незалежними від орієнтації майданчиків. У результаті при оцінці міцності матеріалу замість розгляду 9 компонентів напруженого стану, що залежать від орієнтації елементарних площадок, можна розглядати всього 3 ( 1> 2> 3).

При роботі конструкції під навантаженням деякі точки знаходяться в умовах плоского або просторового

напруженого стану, для яких можливі самі різні співвідношення між головними напруженнями. Для визначення граничного (небезпечного) стану в точці (і тим самим всієї конструкції), слід було б порівняти ці

1 напруження з граничними. Однак, практично це зробити неможливо, оскільки провести експерименти, подібні випробувань на центральний розтяг-стиск до руйнування, довелося б зробити для кожного з

можливих співвідношень між головними напруженнями, не кажучи вже про те, що реалізувати ці співвідношення при випробуваннях технічно важко.

Таким чином, необхідно мати можливість зіставити міцність матеріалу при плоскому та просторовому напруженому стані з результатами випробувань при одноосьовому розтяганні-стисканні.

Це завдання вирішується за допомогою висування гіпотези по якомусь одному критерії, що визначає умову переходу матеріалу в небезпечний стан, що становить основу відповідної теорії міцності.

σz З використанням того чи іншого критерію головні напруження, що виникають в конструкції, вдається пов'язати з

граничними механічними характеристиками, одержуваними при одноосьовому випробуванні. В результаті визначається деяке еквівалентне напруження, що характеризує аналізований напружений стан, який можна

порівнювати з граничним або допустимими напруженнями при одноосьовому розтяганні-стисканні.

■ Критерій руйнування шляхом відриву (крихке руйнування) - Можливе часткове або повне руйнування тіла. Розрізняють руйнування
в'язке і крихке, які можуть проявлятися як одночасно, так і послідовно. Крихке руйнування відбувається в результаті швидкого
розповсюдження тріщини після незначної пластичної деформації або без неї. В останньому випадку руйнування називається ідеально
крихким. При крихкому руйнуванні швидкість поширення тріщини велика (0,2-0,5 швидкості звуку), а злам має кристалічний вигляд. При
квазіхрупкому руйнуванні спостерігається деяка пластична зона перед краєм тріщини. Крихкі тріщини можуть виникати при середніх
напруженнях, що не перевищують межу текучості. Часто тріщини повільно ростуть і процес їх росту може становити до 90% часу	44
"Життя" деталі. Тому має значення не стільки факт виникнення тріщини, скільки темп її зростання.

Лекція 12 (продовження – 12.2)

Поля нормальних і дотичних напружень у вершині тріщини описуються деякими функціями, отримані методами теорії пружності, в які входить коефіцієнт інтенсивності напружень,

мають різні значення в залежності від типу деформації тріщин: I - тріщина нормального відриву;

II - тріщина плоского зсуву;

III - тріщина антиплоского зсуву.

Нижче розглядаються три теорії міцності, що ґрунтуються на критерії руйнування шляхом відриву.

I теорія міцності - Теорія найбільших нормальних напружень: гіпотеза переходу матеріалу в небезпечний стан - досягнення одного з головних напружень граничного (небезпечного) значення.

З використанням цього критерію

1

3

eкв

1

R

- при

Перша умова використовується при 1> 2> 3 > 0,

умова міцності має вигляд:

1

3

eкв

3

R

- при

друга – при 3 < 0, якщо | 3| > | 1|

Теорія враховує лише одне з головних напружень, експериментально підтверджується лише для крихких матеріалів за умови,

що одне з головних напружень значно більше за інших.

II теорія міцності - Теорія найбільших деформацій: гіпотеза переходу матеріалу в небезпечний стан - досягнення

деформаціями граничного (небезпечного) значення.

Тут при обчисленні максимальної деформації беруть участь всі три головні

З використанням цього критерію

max

o

o

.

умова міцності має вигляд:

напруження:

1

E

Отже, умова міцності,

max

E 1 ( 2 3 ) .

eкв 1

( 2

3 ) R.

виражена через головні напруження набуває вигляду:

Теорія враховує всі три головні напруження, але експериментально підтверджується лише для крихких матеріалів за умови, що всі головні напруження негативні.

Таким чином, I і II теорії міцності можуть застосовуватися лише для крихких матеріалів. Зауважимо, що крихкі матеріали часто мають різні механічні характеристиками при розтягуванні і стисненні. Тому в цих випадках необхідно використовувати відповідні розрахункові (допустимі) напруження.

Теорія міцності Мора - використовує припущення, що напруження 2 мало впливає на міцність матеріалу (в межах 15%). Таким чином розрахунок

міцності в загальному випадку тривісного напруженого стану зводиться до розрахунку міцності при двохосьовому напруженому стані. Це не означає, що в умові для II теорії просто слід прирівняти 2 нулю. Тут розрахункове напруження визначається з урахуванням двох випробувань:

на розтяг - р і на стиск - с.

45

Лекція 12 (продовження – 12.3)

Суть теорії Мора в наступному: Нехай відомі дані про небезпечні стани матеріалу при декількох різних співвідношеннях між

напруженнями 3 і 1. Зображуючи кожне з станів колами Мора отримаємо деяке сімейство таких кіл:

Одноосне

для двовісного напруженого стану - круги чорного кольору;

для одноосьових розтягування і стиснення - кола червоного кольору;

стиснення

+

для чистого зсуву - коло синього кольору.

Одноосне

Для матеріалів, опір яких при стисненні більше, ніж при розтягу, огинає

розтягування

граничних напруг (пунктирна крива) наближається до позитивної осі абсцис

і перетинає її в точці A, відповідної Двовісний рівномірному розтягування.

-

A +

Експерименти показують, що при всебічному стисканні матеріал не руйнується при будь-яких,

як завгодно великих напруженнях. Тому огинаюча пряма не перетинає вісь абсцис при стискаючих

напруженнях.

Зменшуючи кола граничних напружень в n раз (n - коефіцієнт запасу), отримаємо область,

-

відповідну допустимим (безпечним) напруженим станам.

Двовісний

Оскільки отримати достатньо велика кількість експериментальних даних важко, зазвичай

Двовісний

Чисте

напружений

обмежуються лише двома випробуваннями (на розтягування і на стискування) і огинаючі криві

напружений

зрушення

стан

замінюють прямими, дотичними до кіл Мора, побудованим за цим випробуванням:

стан (стиск)

+

(розтягнення) Для такої спрощеної діаграми граничних напружених станів можливо отримати

аналітичну умову міцності з подібності прямокутних трикутників:

-

A

+

0.5 с

0.5 р

0.5 р

0.5 1

3

Скоротимо на 0.5 і перемножимо:

0.5 с

0.5 р

0.5 1

3

0.5 р

р c 1 c

3 р

с

р

1 c

р c

3 р

3 1

Після скорочення, складання і скорочення

0.5 с

0.5

на 2 отримаємо:

р c 1 c

3 р 0

Теорія Мора добре

р

узгоджується

0.5( 3- 1) Звідси співвідношення, яке задовольняє лінії

з експериментальними

0.5 с-0.5 р

граничних циклів:

р

даними

0.5 р

р .

1

3

при σ > 0, σ < 0.

c

1

3

0.5 с

Отже, умова

Недоліком теорії

Мора є неврахування

0.5( 3+ 1)

міцності має вигляд:

р

eкв

1

3

р .

проміжного головного

напруження σ .

с

46

2

Лекція 12 (продовження – 12.4)

■ Критерій пластичного стану - При випробуваннях матеріалів було виявлено, що в пластичному стані максимальне дотичне напруження має одне і те ж значення для даного матеріалу. У результаті, в якості наступної гіпотези переходу матеріалу в граничний стан можна вибрати досягнення найбільших дотичних напружень граничного (небезпечного) значення (критерій пластичності). Ця гіпотеза лягла в основу III теорії

міцності.

З використанням цього критерію умова міцності має вигляд:

						1			3				0				Т
					max																		eкв 1 3 Т
									2				2			2
У разі плоского				x y					1
	1									( x			y )2					4 yx2 .
напруженого стану:
				2					2
																								eкв ( x y )2			4 yx2 Т
				x y					1
		3								(						)2		4 2 .
				2					2			x			y					yx			При згині з крученням:				eкв зг2			4 кр2	R

Експериментальні дані показують хороший збіг результатів для пластичних матеріалів. Недоліком III теорії, як і вище вказаних теорій,

єневрахування середнього головного напруження 2 .

■IV теорія міцності (енергетична) - Першою спробою зв'язати всі три головні напруження було висунення гіпотези переходу в граничний стан питомої потенційної енергії деформації деякого граничного значення. Експерименти показали, що при всебічному стисканні, пластичні деформації не виникають, хоча при цьому накопичується велика питома потенційна енергія. У зв'язку з цим була висунута гіпотеза про те, що граничний стан обумовлюється досягненням граничного значення лише тієї частини питомої потенційної енергії деформації, яка пов'язана зі зміною форми:

uф u uоб ,	де u 1 (					3 3 )
		1 1		2 2								- повна питома потенційна енергія.													1			1		[ 1			( 2			3 )];
	2
																												E
Підстановка узагальненого закону Гука
																												1	[ 2				( 1			3 )];
потенційної енергії:						u				1 ( 12 22 32 2 ( 1 2								2 3 3 1 ))							2	E
дає такий вираз для повної питомої
Питому потенційну енергію, витрачену									2E																			1	[ 3				( 1			2 )].
																									3
																											E
на зміну об'єму, можна отримати з цього					uоб	(1				2 ) 3 02 .
виразу, приймаючи 1 = 2 = 3= о:
																	(1	2 )
								2E								uоб				( 1 2 3 )2 .
			ср 1			( 1						3 )					6E
	Приймемо: o							2
Питома потенційна енергія, що					3					1													(1 2 ) (
			u		u u							( 2	2	2		2 (					))														)2 .		47
витрачається на зміну форми:										2E
				ф			об					1	2	3		1 2				2 3	3 1				6E						1			2		3