Учебное пособие по ТВ и МС

Доверительный интервал (θ~n(1) ,θ~n(2) ) может покрывать параметр θ или нет. Именно в таком смысле нужно понимать случайное событие, заключающееся в том, что доверительный интервал покрывает число θ.

Величина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от значения доверительной вероятности γ (увеличивается с приближением γ к 1).

Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно параметра θ.

Наибольшее отклонение ∆ оценки θ~n от истинного значения параметра θ,

которое возможно с заданной доверительной вероятностью γ, называется

предельной ошибкой выборки.

8.3.1. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии

Пусть случайная величина ξ (можно говорить о генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия

D[ξ] = σ 2 . Из генеральной совокупности делается случайная выборка X1 ,K, X n объема n, которая рассматривается как совокупность n независимых

случайных величин, распределенных так же как ξ. Ранее также обсуждались следующие равенства:

M[X1 ] = K= M[X n ] = M[X ], D[X1 ] = K= D[X n ] = D[X ],

M [ X ] = M [ X ], D[ X ] = D[ X ] . n

Случайная величина X также распределена по нормальному закону (см.

предложение 4.7).

Обозначим неизвестную величину M [ξ] через a и подберем по заданной надежности γ число d > 0 так, чтобы выполнялось условие:

P(

− a

< d )=γ .

(8.8)

X

Так

как случайная

величина

распределена

по

нормальному закону

X

N(a,σ 2

n) , то получаем:

P(

− a

< d )= P(a − d <

< a + d ) =

X

X

a + d − a

a − d − a

d n

= Φ

− Φ

= 2Φ

σ

.

σ

/ n

σ / n

111

Осталось подобрать d таким, чтобы выполнялось равенство						d		n
						2Φ	σ	= γ
d		n		γ
			=		.
или Φ	σ			2

Для любого γ [0,1] можно по таблице найти такое число (квантиль) t, что

Φ(t) = γ 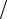2 .

Теперь из равенства

dσn = t

определим d = σnt .

Окончательный результат получим, представив формулу (8.8) в виде:

	σt	< a < X +	σt	= γ
P X −					.
	n
			n

Смысл последней формулы состоит в следующем: с надежностью γ доверительный интервал

	σt	; X +	σt
X −
	n
			n

покрывает неизвестный параметр a = M [ξ] генеральной совокупности. Можно сказать иначе: точечная оценка X определяет значение параметра M [ξ] с точностью d = σt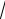n и надежностью γ.

Пример 8.8. Пусть имеется генеральная совокупность с некоторой характеристикой, распределенной по нормальному закону с дисперсией, равной 6,25 . Произведена выборка объема n = 27 и получена выборочная средняя

арифметическая x = 12 . Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью γ = 0,99 .

Решение. Сначала по таблице для функции Лапласа найдем значение t из равенства Φ(t) = γ / 2 = 0,495 . По полученному значению t = 2,58 определим

112

точность оценки d = 2,5 2,58 / 27 ≈1,24 . Отсюда получаем искомый доверительный интервал: (10,76;13,24) .

8.3.2. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии

Пусть ξ – случайная величина, распределенная по нормальному закону с неизвестным математическим ожиданием M [ξ] , которое обозначим буквой a.

Произведем выборку объема n. Определим среднюю выборочную X и несмещенную выборочную дисперсию s2 по известным формулам.

Случайная величина							t =		(X − a)	n	распределена по закону Стьюдента с
(n −1)	степенями свободы.								s
Задача заключается в том, чтобы по заданной надежности γ и по числу
степеней свободы (n −1)							найти такое число tγ, чтобы выполнялось равенство
	(		− a) n
		X
P						< t = γ					(8.9)
			s			γ
или эквивалентное равенство
					s	< a < X + t			s
P X − t				γ				γ	= γ	.	(8.10)
					n
									n

Здесь в скобках написано условие того, что значение неизвестного параметра a принадлежит некоторому промежутку, который и является доверительным интервалом. Его границы зависят от надежности γ, а также от

параметров выборки X и s.

Чтобы определить значение tγ по величине γ, равенство (8.9) преобразуем к виду:

	(		− a) n
		X		≥ t		= 1 − γ
P							.
			s		γ

Теперь по таблице для случайной величины t , распределенной по закону Стьюдента, по вероятности 1 −γ и числу степеней свободы (n −1) находим tγ . Формула (8.10) дает ответ поставленной задачи.

Пример 8.9. На контрольных испытаниях 20-ти электроламп средняя продолжительность их работы оказалась равной 2000 часов при среднем

113

квадратическом отклонении (рассчитанном как корень квадратный из исправленной выборочной дисперсии), равном 11-ти часам. Известно, что продолжительность работы лампы является нормально распределенной случайной величиной. Определить с надежностью 0,95 доверительный интервал для математического ожидания этой случайной величины.

Решение. Величина 1 −γ в данном случае равна 0,05 . По таблице распределения Стьюдента, при числе степеней свободы, равном 19 , находим: tγ = 2,093 . Вычислим теперь точность оценки: 2,093 12 / 20 = 56,6 . Отсюда получаем искомый доверительный интервал: (1943,4; 2056,6) .

8.3.3. Доверительный интервал для дисперсии нормального распределения

Пусть случайная величина ξ распределена по нормальному закону, для которого дисперсия D[ξ] неизвестна. Делается выборка объема n. Из нее определяется исправленная выборочная дисперсия s2. Случайная величина

χ

2

=

(n −1)s2

D[X ]

распределена

по

закону χ2 c (n −1) степенями

свободы. По заданной

надежности γ

можно найти сколько угодно границ χ12

и χ22 интервалов, таких

что

P(χ1

2

< χ 2 < χ2

2 )=γ .

(8.11)

Найдем

χ12 и χ22

из следующих условий:

P(χ 2

≤ χ12 ) =

1 −γ

,

(8.12)

2

P(χ2

≥ χ22 ) =

1−γ

.

(8.13)

2

Очевидно, что при выполнении двух последних условий справедливо равенство (8.11).

В таблицах для случайной величины χ12 и χ22 обычно дается решение

уравнения P(χ2	≥ χq2 ) = q .	Из такой таблицы по заданной величине q и по
числу степеней	свободы	(n −1) можно определить значение χq2 . Таким

образом, сразу находится значение χ22 в формуле (8.13). Для определения χ12 преобразуем (8.12):

114

	P(χ 2 ≥ χ12 ) = 1 −	1 − γ	=		1 + λ	.
		2		2

Полученное равенство позволяет определить по таблице значение χ12 .

Теперь, когда найдены значения χ12 и χ22 , представим равенство (8.11) в виде

	χ	2	<	(n −1)s2	< χ	2		= γ
P		1				2			.
				D[X ]

Последнее равенство перепишем в такой форме, чтобы были определены границы доверительного интервала для неизвестной величины D[X ] :

	(n −1)s2	(n −1)s2
	2 < D[X ] <			= γ .
P		2
	χ2	χ1

Отсюда легко получить формулу, по которой находится доверительный интервал для стандартного отклонения:

P

(n −1)s < D[X
χ	2
	2

] <	(n −	1)s		(8.14)
	χ1	2	= γ .

Пример 8.10. Будем считать, что шум в кабинах вертолетов одного и того же типа при работающих в определенном режиме двигателях – случайная величина, распределенная по нормальному закону. Было случайным образом выбрано 20 вертолетов, и произведены замеры уровня шума (в децибелах) в каждом из них. Исправленная выборочная дисперсия измерений оказалась равной 22,5. Найти доверительный интервал, накрывающий неизвестное стандартное отклонение величины шума в кабинах вертолетов данного типа с надежностью 98%.

	Решение. По числу степеней свободы, равному 19 , и			по вероятности
(1 − 0,98) / 2 = 0,01 находим из			таблицы распределения	χ2	величину
χ22	= 36,2	. Аналогичным образом для вероятности (1 + 0,98) / 2 = 0,99			получаем
χ12	= 7,63	. Используя формулу	(8.14), получаем искомый	доверительный
интервал: (3,44; 7,49) .

Упражнение 8.4. Определить с надежностью 0,95 доверительный интервал для параметра θ равномерного на [0,θ] распределения.

115

Глава 9. Проверка статистических гипотез

На практике часто приходится на основе выборочных наблюдений проверять различные предположения относительно генеральной совокупности. Процедуру сопоставления выдвинутых гипотез с выборкой и решения вопроса относительно приемлемости этих гипотез называют проверкой гипотез.

9.1. Статистическая гипотеза и общая схема ее проверки

Определение 9.1. Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.

Примеры статистических гипотез:

-нормально распределенная случайная величина ξ имеет генеральную среднюю, равную a;

-нормально распределенная случайная величина ξ имеет дисперсию, равную σ2;

-выборка x1 ,K, xn взята из нормально распределенной генеральной совокупности.

Гипотезы делятся на параметрические и непараметрические. Гипотеза называется параметрической, если в ней содержится некоторое утверждение о значении одного или нескольких параметров распределения известного вида. В непараметрической гипотезе заключается утверждение обо всем распределении.

В свою очередь параметрические гипотезы бывают простыми и сложными. Простая гипотеза, в отличие от сложной, полностью определяет теоретическую функцию распределения случайной величины. Например, гипотезы «вероятность появления события в схеме Бернулли равна 1/2», «закон

распределения случайной величины нормальный с параметрами a = 0, σ 2 =1» являются простыми, а гипотезы «вероятность появления события в схеме Бернулли заключена между 0,3 и 0,6», «закон распределения не является нормальным» − сложными.

Проверяемую гипотезу обычно называют основной (или нулевой) и обозначают H0. Наряду с нулевой гипотезой H0 рассматривают альтернативную (или конкурирующую) гипотезу H1, являющуюся логическим отрицанием (дополнением) H0. Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез. Правило, по которому гипотеза H0 отвергается или принимается,

называется статистическим критерием.

Определение 9.2. Процедура обоснованного сопоставления высказанной гипотезы с имеющейся выборкой x1 ,K, xn , осуществляемая с помощью того

116

или иного статистического критерия, называется статистической проверкой гипотезы.

Результат такого сопоставления может быть как отрицательным (данные наблюдения противоречат выдвинутой гипотезе, следовательно, от нее надо отказаться), так и положительным (наблюдения не противоречат высказанной гипотезе, и поэтому ее можно принять в качестве одного из решений).

Неотрицательный результат статистической проверки гипотез не означает, что высказанное нами предположительное утверждение является наилучшим. Могут также существовать другие гипотезы, которые не будут противоречить тем же эмпирическим данным.

Принятая в этом случае гипотеза будет рассматриваться как достаточно правдоподобное, не противоречащее опыту утверждение.

Статистические критерии проверки гипотез разнообразны, но у них единая

логическая схема построения критерия, которая укладывается в 5 этапов.

Этап 1. Выдвигается основная гипотеза H0.

Этап 2. Задается уровень значимости критерия α. Любое статистическое решение, принимаемое на основе ограниченного ряда наблюдений, сопровождается, хоть и малой, вероятностью ошибочного заключения. Именно в доле случаев α гипотеза H0 может быть отвергнута при условии, что она верна. Такие ошибки называют ошибками 1-го рода.

Или, наоборот, в доле случаев β мы можем принять гипотезу H0, в то время как она ошибочна. Эти ошибки являются ошибками 2-го рода.

При фиксированном объеме выборки n величины вероятностей α или β мы можем выбирать самостоятельно. Если есть возможность сколь угодно увеличивать n, то теоретически можно добиться как угодно малых ошибок α и β при любой фиксированной альтернативной гипотезе H1.

Определение 9.3. Вероятность α допустить ошибку 1-го рода, т.е. отвергнуть гипотезу H0, когда она верна, называется уровнем значимости

критерия и определяется как α = P(H1 \ H0 ) .

Чем весомее для исследователя потери от ошибочного непринятия гипотезы H0, тем меньшее α необходимо выбирать. Обычно пользуются стандартными значениями α (0,1; 0,05; 0,025; 0,01; 0,005; 0,001).

Пример 9.1. Величина α = 0,05 означает, что в среднем в 5 случаях из 100 при использовании данного статистического критерия будет ошибочно отвергаться справедливая основная гипотеза H0.

Этап 3. Задается некоторая функция результатов наблюдения –

критическая статистика

117

ψкр =ψ(x1 ,K, xn ) .

(9.1)

Как функция наблюдений эта критическая статистика также является случайной величиной и в предположении справедливости H0 подчинена некоторому хорошо изученному (затабулированному) закону распределения с

плотностью вероятности ϕψкр (x) .

Замечание 9.1. Содержательный смысл критической статистики – мера расхождения имеющейся в распоряжении исследователя выборки с основной гипотезой H0. Например, в гипотезе об однородности двух выборок случайных

величин ξ и η критическая статистика ψкр суть мера различия между функциями распределения Fξ (x) и Fη (x) .

Определение 9.4. Статистикой называется любая (измеримая) функция θ = θ(x1,L, xn ) от выборки данных.

Этап 4. Из статистических таблиц распределения ϕψкр (x) или расчетным

путем находятся						квантили уровня α / 2 и 1−α / 2 или процентные точки
ψ	α	) 100%	и	ψα	100%	, являющиеся соответственно нижней ψкр.н и верхней ψкр.в
(1−	2			2

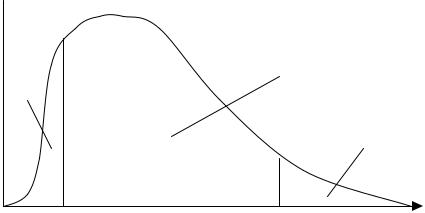
критическими точками (границами). Они делят всю область допустимых значений ψкр на области (рис. 9.1): неправдоподобно малых (I); правдоподобных (II); неправдоподобно больших (III).

Область принятия гипотезы H0 определяется как доверительный интервал для ψкр , который формируется на основе закона распределения статистики

ϕψкр (x) при уровне доверительной вероятности p =1 −α .

Различают односторонние и двухсторонние критерии. Для одностороннего критерия область принятия основной гипотезы может иметь ограничение только с одной стороны (сверху или снизу). При этом область

значений статистики θкр разбивается на две: область правдоподобных и

область неправдоподобно больших или неправдоподобно малых значений. Для двухстороннего критерия область принятия гипотезы H0 имеет два

ограничения – сверху и снизу.

Этап 5. Определяется расчетное значение критической статистики ψкррасч

подстановкой в (9.1) конкретных выборочных значений x1 ,K, xn или

118

некоторых функций от них. Если окажется, что ψкррасч принадлежит области

правдоподобных значений, то гипотеза H0 верна, т. е. не противоречит выборочным данным. В противном случае H0 отвергается с ошибкой 1-го рода

α. Отвержение H0 означает, что ψкррасч не подчиняется закону распределения ϕψкр (x) . Ошибка 2-го рода возникает, если принимается H0, в то время когда она неверна. Ее вероятность β равна β = P(H0 \ H1 ) .

ϕψкр (x)

		p = 1−α
α/2	H0
			α/2
I	II	III
ψкр.н		ψкр.в	x

Рис. 9.1. График плотности вероятности критической статистики с выделением областей принятия и непринятия гипотезы H0

Определение 9.5. Вероятность (1 − β) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу H0, когда она неверна, называется мощностью критерия.

Замечание 9.2. Очевидно, что из двух критериев, характеризующихся одинаковой вероятностью α отвергнуть в действительности правильную гипотезу H0, следует предпочесть тот, который сопровождается меньшей ошибкой 2-го рода (или большей мощностью).

Замечание 9.3. Принцип проверки статистической гипотезы не дает доказательства ее верности или неверности.

Принятие гипотезы H0 в сравнении с альтернативной H1 не означает, что мы уверены в абсолютной правильности H0 или, что высказанное в гипотезе H0 утверждение является наилучшим, единственно подходящим. Просто гипотеза H0 не противоречит имеющимся у нас выборочным данным. Таким же свойством, наряду с H0, могут обладать и другие гипотезы. Более того, возможно, что при увеличении объема выборки n либо при испытании H0 против другой альтернативной гипотезы H2 гипотеза H0 будет отвергнута. Так

119

что принятие гипотезы H0 следует расценивать не как раз и навсегда установленный, абсолютно верный содержащийся в ней факт, а лишь как достаточно правдоподобное, не противоречащее опыту утверждение.

По своему прикладному содержанию статистические гипотезы можно разделить на следующие основные типы:

-о типе законе распределения исследуемой случайной величины;

-об однородности выборок;

-о числовых характеристик случайных величин;

-о стохастической независимости элементов выборки;

-об общем виде модели, описывающей статистическую зависимость между признаками.

Ниже рассмотрим основные гипотезы из первых четырех типов. Последняя группа статистических гипотез об общем виде модели статистической зависимости между признаками рассматривается в курсе «Эконометрика».

9.2. Критерии согласия

Критерии согласия предназначены для статистической проверки гипотез о соответствии эмпирического распределения выборки данных выбранной модели теоретического закона распределения.

Пусть выдвинута гипотеза о том, что случайная выборка из генеральной совокупности может быть описана некоторой моделью с функцией

распределения Fmod (x, Θ) , где Θ = (θ1 ,K,θK ) − вектор параметров, которые

могут быть как известны, так и неизвестны.

Большинство критериев проверки согласия основаны на использовании меры расстояний между анализируемой эмпирической функцией распределения Fn (x) , определенной по выборке объема n, и гипотетической

модельной Fmod (x, Θ) .

9.2.1. Критерий согласия χ2−Пирсона

Критерий согласия χ2−Пирсона позволяет осуществлять проверку гипотезы о согласии, когда параметры модели неизвестны. Неизвестные параметры модели могут быть заменены в модели их оценками, полученными по выборке, одним из точечных методов оценивания (см. § 8.1).

Критерий согласия χ2−Пирсона требует, чтобы:

-объем выборки был не слишком малым;

-выборка должна быть сгруппирована;

120