Учебное пособие по ТВ и МС

Вычислим по выборке оценки: s2 = 23,89, q2(n) = 30,31. Следовательно,

ψ расч = 30,31 = 1,27 . 23,89

Т.к. ψ расч ≥ψкр.н , то то H0 не отвергается и элементы выборки можно считать случайными и независимыми.

Упражнение 9.6. Выборочное исследование возраста покупателей компактдисков в одном из магазинов дало следующие результаты:

20, 20, 32, 27, 40, 24, 23, 18, 16, 15, 18, 26, 19,17, 19, 18, 23.

Проверить гипотезу о стохастической независимости элементов выборки для уровня значимости α = 0,05 с помощью критериев «восходящих» и «нисходящих» серий и Аббе.

141

Раздел 3. ОСНОВНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОГО АНАЛИЗА

В предыдущих главах были даны основные понятия и определения теории вероятностей и математической статистики. Как ни парадоксально, но можно сказать, что теперь приступим к освоению статистического анализа. Теория вероятностей и математическая статистика представляют лишь теоретический фундамент для изучения статистических зависимостей, но не ставят своей целью установление причинной связи.

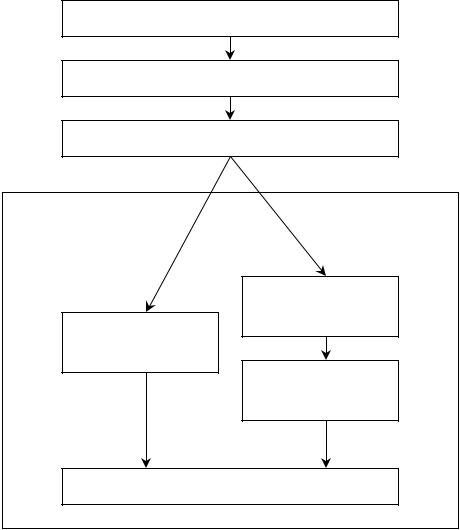
Общую схему основных этапов статистического анализа можно изобразить в виде следующей схемы:

Содержательный анализ

Составление плана сбора исходных данных

Получение исходных данных

Построение и анализ статистических зависимостей

Корреляционный анализ

Дисперсионный

анализ

Регрессионный

анализ

Интерпретация результатов

Как было отмечено во введении к разделу 2, математическая статистика, так же как и теория вероятностей, являются формально-логическими системами.

142

Практикой применения теоретико-вероятностных положений при решении конкретных задач занимается уже не математическая, а прикладная статистика, методы статистического анализа. Здесь трудно провести границу, где заканчивается математическая статистика, и начинается прикладная статистика.

Экономические процессы носят вероятностный (а часто, неопределенный) характер. Поэтому возрастает роль вероятностно-статистических методов в изучении экономики. В связи с этим, представляется целесообразным закончить изучение данного курса рассмотрением основных методов статистического анализа, получивших наибольшее распространение при изучении экономики.

Вопросы, связанные с практическим освоением статистического анализа данных, а также изучение других методов статистического анализа, рассматриваются в курсах «Статистика», «Эконометрика» и «Многомерные статистические методы».

Задачей изучения данного раздела является изучение основных методов, используемых в статистическом анализе социально-экономических явлений.

Главы этого раздела:

•10. Дисперсионный анализ

•11. Корреляционный анализ

•12. Регрессионный анализ

143

Глава 10. Дисперсионный анализ

В § 9.4 была рассмотрена проверка значимости различия выборочных средних двух совокупностей. На практике часто возникает необходимость обобщения задачи на случай нескольких (более чем двух) совокупностей. Эта проблема решается с помощью дисперсионного анализа.

Идея дисперсионного анализа, как и сам термин «дисперсия», принадлежит английскому статистику Р. Фишеру. Метод был разработан в 1920-х годах.

Дисперсионный анализ позволяет оценивать влияние на количественный отклик Y неколичественных факторов (X1, …, Xn) с целью выбора среди них наиболее важных. Такими качественными факторами могут быть тип оборудования или технологического процесса, вид сырья, способ обработки и другие условия, влияющие на выходные характеристики изделия.

10.1. Основные понятия дисперсионного анализа

Определение 10.1. Дисперсионный анализ – метод статистического анализа, позволяющий определить достоверность гипотезы о различиях в средних значениях на основании сравнения дисперсий распределений.

В процессе наблюдения за исследуемым объектом качественные факторы произвольно или заданным образом изменяются. Конкретная реализация фактора (например, определенный температурный режим, выбранное оборудование или материал) называется уровнем фактора или способом обработки. Модель дисперсионного анализа с фиксированными (или систематическими) уровнями факторов называют моделью I, модель со случайными факторами – моделью II. Благодаря варьированию фактора можно исследовать его влияние на величину отклика. В настоящее время общая теория дисперсионного анализа разработана для моделей I.

Пример 10.1. Пусть необходимо выяснить, имеются ли существенные различия между партиями изделий по некоторому показателю качества, т.е. проверить влияние на качество одного фактора – партии изделий. Если включить в исследование все партии изделий, то влияние уровня такого фактора систематическое (модель I), а полученные выводы применимы только к тем отдельным партиям, которые привлекались для исследования; если же включить только отобранную случайно часть партий, то влияние фактора случайное (модель II).

Дисперсионный анализ основан на разложении общей дисперсии (вариации) отклика на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Оценив влияние факторов, дисперсионный анализ позволяет выбрать среди них наиболее важные.

144

В зависимости от количества факторов, включенных в анализ, различают одно- и многофакторный дисперсионный анализ.

Основными схемами организации исходных данных с двумя и более факторами являются:

1)перекрестная классификация, характерная для моделей I, в которых каждый уровень одного фактора сочетается при планировании эксперимента с каждой градацией другого фактора;

2)иерархическая (гнездовая) классификация, характерная для модели II, в

которой каждому случайному, наудачу выбранному значению одного фактора соответствует свое подмножество значений второго фактора.

10.2.Однофакторный дисперсионный анализ

10.2.1.Аддитивная модель однофакторного дисперсионного анализа

Пусть измеряются размеры Y однотипных деталей, изготавливаемых на параллельно работающем оборудовании. Все наблюдения отклика представляются в виде матрицы наблюдений (табл. 10.1).

Таблица 10.1

Номер		Уровни фактора A (способы обработки)
наблюдения	1		2	…	j	…		n
1	y11		y12	…	y1j	…		y1n
2	y21		y22	…	y2j	…		y2n
…	…		…	…	…	…		…
i	yi1		yi2	…	yij	…	yin
…	…		…	…	…	…		…
m	ym1		ym2	…	ymj	…	ymn

Здесь n – число станков или уровней фактора A, влияние которого на размеры деталей Y исследуется при дисперсионном анализе.

На каждом j-м уровне производится m наблюдений. Заметим, что в общем случае объемы выборок на каждом уровне могут не совпадать.

Для описания данных матрицы наблюдений при дисперсионном анализе используется аддитивная модель. Каждое наблюдение отклика yij представляется в виде суммы вклада воздействия фактора aj и независимой от вклада фактора случайной величины (возмущения) εij

yij = a j + εij = µ + τ j + εij , i =	1, m	,	j =	1, n	.	(10.1)
Величина a j = µ + τ j является			средним значением			отклика (размера

деталей) для j-го уровня фактора (j-го станка). Эта неслучайная величина – результат действия соответствующего способа обработки.

145

	1	n
Величина µ является общим средним уровнем отклика µ =		∑a j
	n	j=1

Величина τ j = a j − µ − отклонение от среднего уровня при j-й обработке,

n

или эффект, обусловленный влиянием j-го фактора, ∑τ j = 0 .

j=1

Предложение 10.1. Основные предпосылки дисперсионного анализа:

1.Математическое ожидание возмущения εij M[εj] = 0 для любых j.

2.Возмущения εij взаимно независимы.

3.Дисперсия переменной Y (или возмущения ε) постоянна для любых i, j.

4.Переменная Y (или возмущение ε) имеет нормальный закон распределения. #

Одинаково распределенные случайные величины εij отражают присущую наблюдениям внутреннюю изменчивость. Они характеризуют эффект случайности или влияние неучтенных аддитивной моделью (10.1) факторов.

Таким образом, общая вариация отклика yij − µ может быть разложена на

составляющую τ, которая характеризует влияние фактора и случайную часть от воздействия неучтенных факторов.

Стратегия дисперсионного анализа заключается в следующем.

Проверяется нулевая гипотеза об отсутствии эффектов обработки H0: τ1 =τ2 =K=τn = 0. Если H0 справедлива, то все данные матрицы наблюдений принадлежат одному и тому же распределению, т.е. данные однородны: a1 = a2 =K= an . Различие между столбцами (для разных станков или уровней

фактора) объясняется лишь эффектом случайности. На этом однофакторный дисперсионный анализ заканчивается.

Если H0 отвергается и принимается альтернативная гипотеза H1: a1 ≠ a2 ≠K≠ an , различие в средних значениях отклика обусловлено не только эффектом случайности, но и действием исследуемого фактора. В этом случае строятся доверительные интервалы для воздействий фактора a j , j = 1, n .

10.2.2. F-отношение. Базовая таблица однофакторного дисперсионного анализа

n

m

Пусть Q = ∑∑( yij −

)2 – общая (полная) сумма квадратов отклонений

y

j=1 i=1

отдельных

наблюдений

отклика

yij относительно

общей

средней

,

где

y

1 n

m

y =

y

µ

µ ≈ y

∑∑ ij

является

оценкой

общего среднего

. После

ряда

,

mn j=1 i=1

146

преобразований можно получить следующее основное тождество дисперсионного анализа о разбиении величины Q на слагаемые:

n

m

n

n m

∑∑( yij −

)2

= m∑(

j −

)2

+ ∑∑( yij −

j )2 ,

y

y

y

y

(10.2)

j=

i=1

j=1

j= i=1

1442443

1442443

1442443

Q

Qмод

Qост

1

m

где

j

=

∑ yij

y

− средние значения столбцов матрицы наблюдений, т.е.

m i=1

средняя арифметическая m наблюдений j-го уровня. Замена индекса точкой

означает результат суммирования по этому индексу. Величина y j является оценкой воздействия фактора на j-м уровне aj, a j ≈ y j .

Слагаемое Qмод в (10.2) − сумма квадратов между группами наблюдений,

характеризует расхождения между уровнями фактора a j , j = 1, n , т.е. вклад в

общую сумму квадратов, обусловленный рассеянием за счет исследуемого фактора. Этот вклад можно считать обусловленным введенной моделью.

Слагаемое Qост − сумма квадратов внутри групп наблюдений (или остаточное рассеяние), характеризует случайную изменчивость наблюдений внутри групп за счет неучтенных факторов.

Результаты вычислений представляют в виде базовой таблицы однофакторного дисперсионного анализа:

Таблица 10.2

	Источник дисперсии	Сумма квадратов	Число степеней	Средний квадрат
			свободы	(оценка дисперсии)
	Между группами			2				Qмод
	(фактор A)	Qмод	n−1	sмод		=
								n −1
	Внутри групп			2				Qост
	(остаточное рассеяние)	Qост	n(m−1)	sост	=
							n(m −1)
	Полная (общая)	Q = Qмод + Qост	nm−1	s2y	=			Q
							nm −1

Число степеней свободы в общем случае равно числу независимых наблюдений, уменьшенному на число параметров, оцениваемых по этим наблюдениям при вычислении статистики. Например, при вычислении Qост

число наблюдений равно nm, число оцениваемых параметров y j равно n,

поэтому число степеней свободы равно n(m–1). Зная суммы квадратов Q, Qмод и Qост и их число степеней свободы, вычисляются соответствующие дисперсии:

общую	s2y , межгрупповую sмод2	и внутригрупповую sост2 , причем
s2y	= sмод2 + sост2 .	(10.3)

147

Для		проверки нулевой гипотезы			H0 об отсутствии влияния фактора
(эффектов обработки) используется критическая статистика, называемая F–
отношением, равная
ψкр	=		s2
			мод	.	(10.4)
			2
			sост

Предложение 10.2. Предельное распределение статистики ψкр как случайной величины в случае справедливости проверяемой гипотезы H0 стремится к F−распределению Фишера F (n1, n2 ) с n1 и n2 числом степеней

свободы	lim Fψкр (x) = F(n1 −1, n2 −1)	, где n1 = n–1, n2 = n(m–1). #
	n1 ,n2 →∞

Чем сильнее нарушается гипотеза H0, тем большую тенденцию к возрастанию проявляет F–отношение. Для уровня значимости α находится критическое значение Fα. При расчетном значении F–отношения ψрасч > Fα(n–1, n(m–1)) нулевая гипотеза H0 отвергается и делается заключение о существенном влиянии фактора A.

F–отношение (10.4) позволяет обнаружить, значимо ли различаются способы обработки. Если гипотеза H0 отклонена, то дальнейший анализ связан

с оцениванием воздействий a j , j = 1, n фактора A. Только вычислив

доверительные границы для воздействий фактора, можно сказать, пересекаются ли некоторые из интервалов, и упорядочить по значениям воздействия aj.

Их точечными оценками являются внутригрупповые средние y j , которые

					σ 2
	имеют распределения			N a j ,	ост		, где σост2	≈ sост2 .
					m
	Статистика	t =	y j − a j		m подчиняется распределению Стьюдента с n(m–
				sост

1) степенями свободы. Тогда доверительный интервал для aj при уровне значимости α имеет вид

y j − a j < sостm t1−α ,

где t1−α − квантиль уровня 1−α распределения Стьюдента.

Если доверительные интервалы для всех aj не пересекаются, можно ранжировать способы обработки по степени их влияния на размеры деталей Y.

Пример 10.2. Имеются четыре партии сырья для текстильной промышленности. Из каждой партии отобрано по пять образцов и проведены

148

испытания на определение величины разрывной нагрузки. Результаты испытаний приведены в таблице 10.3.

Таблица 10.3 Значения разрывной нагрузки (кг/см2)

Номер образца		Номер партии
	1		2	3	4
1	200		190	230	150
2	140		150	190	170
3	170		210	200	150
4	145		150	190	170
5	165		150	200	180

Необходимо выяснить для уровня значимости α = 0,05, существенно ли влияние различных партий сырья на величину разрывной нагрузки.

Решение. Имеем m = 5, n = 4. Найдем средние значения разрывной

нагрузки y j для каждой партии:

y1 = (200 +140 +170 +145 +165) / 5 = 164 (кг/см2)

и аналогично y2 = 170 , y3 = 202 , y4 = 164 (кг/см2).

Общее среднее значение разрывной нагрузки y всех образцов равно:

y = (200 +140 +170 +K+150 +170 +180) / 20 = 175 (кг/см2).

Сумма квадратов между группами наблюдений Qмод согласно (10.2) равна:

4					)2 = 5[(164 −175)2 + (170 −175)2 + (202 −175)2 +
Qмод = 5∑(			j −
		y		y
j=1
							+ (164 −175)2 ]= 5 996 = 4980 .
Сумма квадратов внутри групп наблюдений Qост равна:
4	5
Qост = ∑∑( yij −							j )2 = (200 −164)2 +K+ (165 −164)2 +
						y
j=1	i=1

+(190 −170)2 +K+ (150 −170)2 + (230 − 202)2 +K+ (200 − 202)2 +

+(150 −164)2 +K+ (180 −164)2 = 7270

Тогда полная сумма квадратов отклонений отдельных наблюдений составит Q = Qмод + Qост = 4980 + 7270 = 12250.

Соответствующие числа степеней свободы для этих сумм составят: n–1 = 3; n(m–1) = 4 (5–1) = 16; nm−1 = 4 5–1 = 19.

Определим теперь, используя базовую таблицу однофакторного дисперсионного анализа, межгрупповую и внутригрупповую дисперсии:

	sмод2 =	Qмод		=	4980	= 1660 , sост2	=	Qост	=	7270	= 454,38 .
		n −1			3			n(m −1)		16

В результате имеем фактическое расчетное значение F–отношения

149

ψ расч =	s2	=	1660	= 3,65 .
	мод
	2		454,38
	sост

Критическое значение F−критерия для уровня значимости α = 0,05 найдем из таблицы: F0,05(3; 16) = 3,24.

Поскольку ψ расч > F0,05 (3;16) , то нулевая гипотеза H0 отвергается, т.е. на

уровне значимости α = 0,05 (с надежностью 95%) различие между партиями сырья оказывает существенное влияние на величину разрывной нагрузки.

Упражнение 10.1. На заводе установлено четыре линии по выпуску облицовочной плитки. С каждой линии случайным образом в течение смены отобрано по 10 плиток и сделаны замеры их толщины (мм). Отклонения от номинального размера приведены в таблице:

Линия по выпуску				Номер испытания
плиток	1	2	3	4	5	6	7	8	9	10
1	0,6	0,2	0,4	0,5	0,8	0,2	0,1	0,6	0,8	0,8
2	0,2	0,2	0,4	0,3	0,3	0,6	0,8	0,2	0,5	0,5
3	0,8	0,6	0,2	0,4	0,9	1,1	0,8	0,2	0,4	0,8
4	0,7	0,7	0,3	0,3	0,2	0,8	0,6	0,4	0,2	0,6

Требуется на уровне значимости α = 0,05 установить наличие зависимости выпуска качественных плиток от линии выпуска (фактор A).

10.3. Понятие о многофакторном дисперсионном анализе

Когда на отклик воздействует несколько факторов, каждый из которых принимает конечное число уровней, может возникнуть необходимость рассмотрения многофакторных моделей. Это можно объяснить следующим образом.

Однофакторная модель может оказаться незначимой, если влияние фактора A, определяемое F−отношением, является несущественным на фоне большого внутригруппового разброса sост. Этот разброс может быть вызван не только случайными причинами, но также действием еще одного «мешающего» фактора B. Фактор B дополнительно включается в модель, чтобы попытаться уменьшить действие неучтенных факторов и повысить влияние на отклик закономерных причин. Аналогично возникает необходимость рассмотрения трех- и многофакторных моделей.

Соответственно, в процессе дисперсионного анализа варьируется не один, а несколько факторов. При полном многофакторном дисперсионном анализе отклик наблюдается для каждого сочетания уровней изучаемых факторов.

150