Учебное пособие по ТВ и МС

- количество ni , i =1, L попаданий в каждый интервал должно быть не

менее 4. В противном случае соседние интервалы необходимо объединить в один, не забывая при этом корректировать L.

Рассмотрим последовательность критерия согласия χ2−Пирсона.

1-й шаг. Формирование основной и альтернативной гипотез

H0 : Fn (x) = Fmod (x, Θ) , H1 : Fn (x) ≠ Fmod (x, Θ) .					(9.2)
2-й шаг. Задание уровня значимости α.				(ni − npi )	2
			L
3-й шаг. Формирование критической статистики ψкр = ∑						,	где
				npi
			i=1
pi = Fmod (xi+1 ,Θ) − Fmod (xi ,Θ) − теоретическая вероятность попадания						в	i-й
интервал [xi , xi+1 ].
Предельное распределение статистики ψкр при n → ∞ имеет вид
L	(ni − npi )	2
lim ∑			= χ2 (L − S −1) ,
	npi
n→∞ i=1

где S − количество параметров модельного распределения, согласие с которым проверяется, χ2 (L −S −1) − функция χ2−распределения с (L − S −1) числом степеней свободы.

4-й шаг. Определение верхней и нижней критических точек по таблице процентных точек χ2−распределения:

ψкр.в = χα2	100%		(L − S −1) , ψкр.н = χ 2						α	(L − S −1) .
2								(1−	2	) 100%
5-й шаг. Определение расчетного значения критической статистики
L		(ni	− npi )	2
ψ расч = ∑					.							(9.3)
			npi
i=1
Если выполняется условие						χ2	α	) 100%		(L − S −1) ≤ψ расч ≤ χα2	(L − S −1)	,
						(1−	2			2	100%

то гипотеза о согласии H0 верна с ошибкой первого рода α. В противном случае гипотеза H0 отвергается.

121

Отвержение гипотезы H0 в случае слишком маленьких значений

критической статистики,	т.е. при	ψ расч < χ2	α	) 100%	(L − S −1) , на первый взгляд
		(1−	2
противоречит здравому	смыслу.	Однако	надо		отметить, что ψ расч как

статистика также является случайной величиной со своей дисперсией. А значит одинаково неправдоподобными можно считать как слишком большие, так и

слишком малые ψ расч .

Причинами возникновения слишком малых ψ расч могут быть как неудачный выбор Fmod (x, Θ) (например, при искусственном завышении числа

параметров модели или ошибочной модели), так и некорректное проведение эксперимента при деформировании выборки, например стремление искусственно «подогнать» эмпирические данные под результат.

Замечание 9.4. Использование данного критерия основано на теореме Пирсона–Фишера, которая утверждает, что если гипотеза H0 (см. (9.2)) истинна, то при некоторых достаточно общих условиях распределение критической

статистики ψ расч , определяемой по формуле (9.3), сходится (при n → ∞ ) к χ2 (L −S −1) −распределению.

Замечание 9.5. Критерий согласия χ2−Пирсона достаточно эффективен, когда все ожидаемые частоты npi ≥10, i =1, L .

Пример 9.2. Проверить с помощью критерия χ2−Пирсона согласованность эмпирического распределения рабочих по выработке (таблица 9.1), с нормальным законом на уровне значимости α = 0,05 .

			Таблица 9.1
	Выработка в		Количество
№№	отчетном году в %		рабочих, ni
	к предыдущему, xi
1	94	– 100	3
2	100	– 106	7
3	106	– 112	11
4	112	– 118	20
5	118	– 124	28
6	124	– 130	19
7	130	– 136	10
8	136	– 142	2
	Всего		100

Решение. Параметры нормального закона – математическое ожидание a и дисперсия σ2 неизвестны, поэтому заменяем их на выборочную среднюю x и

122

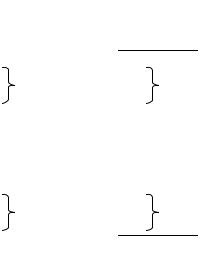
выборочную дисперсию σ~2				(т.к. число	наблюдений n = 100	достаточно
велико), равные			= 119,2 и σ~2	= 9,35 .
		x
Для расчета вероятностей pi попадания случайной величины ξ в интервал
[xi , xi+1 ]	используем функцию Лапласа				в соответствии со	свойством

нормального распределения:

1

x

i+1

− a

x

i

− a

pi (xi ≤ ξ ≤ xi+1 ) =

Φ

− Φ

≈

2

σ

σ

1

x

i+1

− 119,2

x

i

− 119,2

≈

Φ

− Φ

.

2

9,35

9,35

Например,	p1	(94 ≤ ξ ≤ 100) =	1		100 − 119,2				94 − 119,2		=
			2	Φ		9,35		− Φ	9,35

=	1	[Φ(−2,05) − Φ(−2,69)] =	1	(−0,9596 + 0,9928) = 0,0166 , и соответствующая
	2		2

первому интервалу теоретическая частота np1 = 100 0,0166 ≈ 1,7 и т.д. Для определения статистики ψкр удобно составить таблицу:

							Таблица 9.2
№№		[xi , xi+1 ]	ni	pi	npi	(ni−npi)2			(ni − npi )2
									npi
1		94 – 100	3	0,017	1,7
			10		7,6	5,76		0,758
2		100 – 106	7	0,059	5,9
3		106 – 112	11	0,141	14,1	9,61		0,682
4		112 – 118	20	0,228	22,8	7,84		0,344
5		118 – 124	28	0,247	24,7	10,89		0,441
6		124 – 130	19	0,182	18,2	0,64		0,035
7		130 – 136	10	0,087	8,7
			12		11,6	0,16		0,014
8		136 – 142	2	0,029	2,9
	Всего		100	0,990	99,0	−		ψ расч = 2,27

Учитывая, что в рассматриваемом эмпирическом распределении частоты первого и последнего интервалов (n1 = 3, n8 = 1) меньше 4, целесообразно объединить указанные интервалы с соседними (см. табл. 9.2).

Итак, расчетное значение статистики ψ расч = 2,27 . Т.к. новое число

интервалов (с учетом объединения крайних) L = 6, а нормальный закон распределения определяется S = 2 параметрами, то число степеней свободы k = L − S −1 = 6 − 2 −1 = 3 . Соответствующие верхнее и нижнее критические значения статистики определим из статистической таблицы:

123

ψкр.в = χ0,052		(3) = χ0,0252 (3) = 9,35 ,	ψкр.н = χ2	0,05 (3) = χ0,9752 (3) = 0,22 .		Т.к.
			1−
2				2
χ02,975 (3) ≤ψ расч		≤ χ02,025 (3) , гипотеза	о выбранном теоретическом нормальном
законе с параметрами N(119,2; 87,48) согласуется с опытными данными.

9.2.2. Критерий согласия Колмогорова−Смирнова

Критерий согласия Колмогорова−Смирнова проверяет гипотезу о согласии при небольшом объеме выборки, когда Fmod (x, Θ) известна полностью, т. е. известны и параметры модели. Рассмотрим последовательность критерия.

1-й шаг. Формулирование основной H0 и альтернативной H1 гипотез (9.2). 2-й шаг. Задание уровня значимости α.

3-й шаг. Формирование критической статистики.

В критерии Колмогорова−Смирнова для введения меры отклонения эмпирического и модельного распределений используются статистика вида

Dn = max Fn (x) − Fmod (x, Θ) .

x

В качестве ψкр	используем функцию
ψкр = n Dn =	n max Fn (x) − Fmod (x, Θ) .	(9.4)
	x

Предложение 9.1. Какова бы ни была функция распределения Fmod (x,Θ) непрерывной случайной величины ξ, распределение ψкр имеет пределом

∞
функцию Κ(ψкр ) = ∑(−1)i e−2i2ψкр2	, не зависящую от вида функции Fmod (x,Θ) . #
i=−∞

Если Fmod (x,Θ) задана с точностью до неизвестных параметров Θ и они оцениваются по конечной выборке размера n, то предельное распределение статистики Dn n уже зависит от Fmod (x,Θ) . При этом статистика ψкр будет зависеть только от формы распределения Fmod (x,Θ) . Если в модельном

распределении есть только параметры сдвига и масштаба, то применимость критерия Колмогорова–Смирнова корректна.

4-й шаг. Из определения функции распределения следует, что при достаточно большом n и любом ψкр > 0 вероятность того, что Dn n примет значение, меньшее ψкр , будет иметь вид

P{D n ≥ψ }=1−Κ(ψ ) =1− ∞ (−1)i e−2i2ψ 2 =α

n кр кр ∑ кр . i=−∞

124

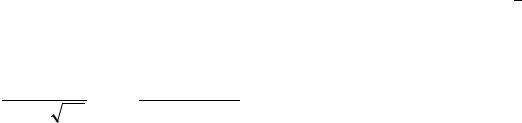
Значение ψкр.в при заданном α можно найти в статистических таблицах. Нижняя критическая граница в данном критерии не используется.

5-й шаг. ψ расч определяется из (9.4) подстановкой значений n и Dn, для конкретных эмпирических данных. Если выполняется условие ψ расч ≤ ψкр.в , то гипотеза о согласии эмпирического распределения и модельного принимается.

Замечание 9.6. Для большого объема выборки, ее нужно сгруппировать и значения Fn (x) и Fmod (x,Θ) определять на границах интервалов группирования.

Применение критерия в принципе возможно лишь тогда, когда теоретическая функция распределения Fmod (x,Θ) задана полностью. Но такой

случай на практике встречается весьма редко. Обычно из теоретических соображений известен лишь вид функции распределения, а ее параметры определяются по эмпирическим данным.

Пример 9.3. Даны результаты исследования отклонения фактического выпуска продукции (тыс. руб.) от планового (план – 1000 тыс. руб.) 400 предприятий в группированном виде:

Таблица 9.3

	Фактический	950-	960-	970-	980-	990-	1000-	1010-	1020-	1030-	1040-
	выпуск	960	970	980	990	1000	1010	1020	1030	1040	1050
	Количество	5	15	60	72	80	60	55	30	20	3
	предприятий

Проверить гипотезу о согласии эмпирического распределения с нормальной моделью по критерию Колмогорова–Смирнова при α = 0,05.

Решение. Параметры нормального закона – математическое ожидание a и дисперсия σ2 неизвестны, поэтому заменяем их на выборочную среднюю x и

выборочную дисперсию σ~2 ,						равные		= 99,45 и σ~2 = 361,998 . Следовательно,
							x
распределение нормальной модели будет иметь вид
p	(x) =	1			−	(x − 997,45)			2
			π	exp		723,996				,
ξ		19,023
			2

	x			x − 997,45
	Fmod (x, Θ) = ∫	pξ ( y)dy = FN (x; 997,45; 19,03)	= 0,5	+ Φ		.
					19,03
	−∞

Результаты вычисления статистики ψ расч сведены в табл. 9.4.

1-й шаг. Формулирование основной H0 и альтернативной H1 гипотез (9.2). 2-й шаг. α = 0,05.

125

3-й шаг. Вид ψкр и ее распределение находим из (9.4) и предложения 9.1.

4-й шаг. Из таблицы значений функции Колмогорова для уровня значимости α = 0,05 определяем ψкр.в = 1,36 .

5-й шаг. Используя данные таблицы 9.4, находим

ψ расч = n max Fn (x) − FN (x; 997,45; 19,03) = 400 0,0317 = 0,634 .

x

Поскольку ψ расч >ψкр.в , то гипотеза H0 отвергается с ошибкой первого рода

α = 0,05.

Таблица 9.4 Результаты вычисления ψ расч для примера 9.3

[x				]										FN (x;		; σ~) =	F (x) − F (x;			; σ~)
									xi −						x
	, x				Fn(x)	z		=		x			Φ(zi)
			i+1																x
							i		σ~
i														= 0,5 + Φ(zi )			n	N
					0			–∞					–0,5	0				0
–∞ – 960					0,0125			–1,97					–0,4756	0,0244				0,0119
960		–	970		0,05			–1,44					–0,4222	0,0778				0,0278
970		–	980		0,2			–0,92					–0,3159	0,1841				0,0159
980		–	990		0,38			–0,39					–0,1517	0.3483				0,0317
990 – 1000					0,58			0,13					0,0517	0,5517				0,0283
1000		–	1010		0,73			0,66					0,2454	0,7454				0,0154
1010		–	1020		0,8675			1,18					0,3810	0,8810				0,0135
1020		–	1030		0,9425			1,71					0,4564	0,9564				0,0139
1030		–	1040		0,9925			2,23					0,4871	0,9871				0,0054
1040 – ∞					1,0			∞					0,5	1,0				0

Упражнение 9.1. Для примера 9.3 проверить гипотезу о согласии эмпирического распределения с равномерным распределением по критериям χ2−Пирсона и Колмогорова–Смирнова при α = 0,05.

9.3. Критерии однородности

При сравнении на однородность различных генеральных совокупностей по выборочным данным ее понимают в различном смысле. Основные гипотезы однородности можно записать в виде:

H0F : F1 (x) = F2 (x) = K= F3 (x) ;

H 0a : a1 = a2 = K = al ;

H 0σ : σ12 = σ 22 = K = σl2 .

Рассмотрим два наиболее распространенных статистических критерия проверки гипотез об однородности анализируемых генеральных совокупностей.

126

9.3.1. Критерий однородности Смирнова

Пусть имеются две выборки объемами n1 и n2. Элементы каждой выборки независимы, непрерывны и сгруппированы в L интервалов. Проверим, принадлежат ли выборки одной генеральной совокупности.

Критерий Смирнова применим при:

-min(n1,n2 ) >50 ;

-данные представлены в группированном виде.

1-й шаг. Формирование основной и альтернативной гипотез

H0 : Fξ (x) = Fη ( y) , H1 : Fξ (x) ≠ Fη ( y) .

2-й шаг. Задание уровня значимости α.

3-й шаг. Формирование критической статистики

L	(µ	i	/ n	−ν	i	/ n	2	)2
ψкр = n1n2 ∑			1						,
			µi +νi
i=1

где µi, νi − количество попаданий в i-й интервал группирования соответственно

			L			2
первой и второй выборок. Если n1 = n2 = n , то ψкр = ∑				(µi		−νi )	.
			i=1		µi	+νi
Предложение 9.2. Предельное распределение критической статистики ψкр
при неограниченном росте объемов выборок					n1 , n2 и в			условиях
справедливости проверяемой гипотезы H0 стремится					к χ2−распределению с
(L −1) числом степеней свободы, т. е. n lim,n →∞ F(ψкр ) = χ2 (L −1) . #
		1	2
4-й	шаг.	Определение критической точки статистического						критерия
ψкр.в = χα2 100% (L −1) , где χα2 100% (L −1) − α-процентная точка χ2−распределения,
которая	может	быть получена с помощью таблиц			процентных			точек для

χ2−распределения. Критерий Смирнова является односторонним. Области неправдоподобно малых значений статистики ψкр нет. Чем меньше расчетное

значение критической статистики, тем более благоприятные условия складываются для принятия гипотезы об однородности двух выборок.

5-й шаг. Определение расчетного значения критической статистики

L	(µ	i	/ n	−ν	i	/ n	2	)2
ψ расч = n1n2 ∑			1						.
			µi +νi
i=1

Если ψ расч ≤ψкр.в , то гипотеза H0 верна, в противном случае H0 отвергается.

127

Пример 9.4. В банке в течение двух дней проводилось исследование времени обслуживания клиентов. Данные представлены в табл. 9.5, где µi, νi − времена обслуживания клиентов в первый и второй дни. Проверить однородность двух группированных выборок – времени обслуживания в первый и второй дни по критерию Смирнова при уровне значимости α = 0,1.

Таблица 9.5 Статистические данные времени обслуживания клиентов в банке

Номер интервала	Время	µi (1-й день)	νi (2-й день)
группирования i	обслуживания (мин)
1	10 – 12	2	2
2	12 – 14	4	4
3	14 – 16	8	9
4	16 – 18	12	13
5	18 – 20	16	16
6	20 – 22	10	8
7	22 – 24	3	3

Решение. Определим из статистической таблицы верхнюю критическую

точку ψкр.в = χ02,1 (7 −1) = χ02,1 (6) = 10,645 .

Расчетное значение критической статистики ψ расч

равно:

+

ψ расч = ∑

(µi −νi )

=

(2 − 2)

+

(4 −

4)

2

+

(8 − 9)

2

+

(12 −13)

2

L

2

2

i=1

µi +νi

4

8

17

25

=

(16 −16)2

+

(10 −8)2

+

(3 − 3)2

= 0,321.

32

18

6

Условие ψ расч ≤ψкр.в выполняется, и H0 верна с ошибкой первого рода 10%.

Упражнение 9.2. Проверить по критерию Смирнова при уровне значимости α = 0,1 однородность группированных выборок – выработки рабочих двух цехов.

				Таблица 9.6
	Выработка в		Количество рабочих
			В первом цехе,	Во втором цехе,
№№	отчетном году в %
	к предыдущему		µi	νi
				5
1	94	– 100	3
2	100	– 106	7	12
3	106	– 112	11	16
4	112	– 118	20	28
5	118	– 124	28	45
6	124	– 130	19	27
7	130	– 136	10	14
8	136	– 142	2	3
	Всего		100	150

128

9.3.2. Критерий Вилкоксона−Манна−Уитни

Критерий Вилкоксона−Манна−Уитни является ранговым и применяется для проверки однородности двух генеральных совокупностей понимаемой в смысле отсутствия различий в значениях параметров положения (средних значений, медиан) соответствующих распределений (но не тождественного совпадения распределений, как в предыдущем критерии). Т.е. речь идет о

проверке гипотез типа H 0a . Распределения проверяемых генеральных

совокупностей неизвестны.

Статистические данные должны быть представлены в негруппированном виде. В критерии возможны два случая. Рассмотрим их последовательно.

Случай А. Пусть имеются две выборки независимых непрерывных

случайных величин

x1 ,K, xn

, y1 ,K, yn

2

, где n1 ≤ 25, n2

≤ 25 .

1

1-й шаг. Формирование

основной

и альтернативной

гипотез

H0 : Fξ (x) = Fη ( y) ,

H1 : Fξ (x) ≠ Fη ( y) .

2-й шаг. Задание уровня значимости α .

n1 +n2

3-й шаг. Формирование критической статистики,

равной ψкр = ∑Ri(1) , где

i=1

Ri(1) − ранги элементов выборки меньшего объема

(n1 ≤ n2 ) .

Суммирование

рангов Ri(1) осуществляется по элементам меньшей выборки.

Предложение

9.3. В условиях справедливости

гипотезы

H0

статистика

n1 +n2

n1

ψкр = ∑Ri(1)

при

n1 → ∞

и

nlim→∞

= c > 0

стремится

к

нормальному

i=1

1

n2

распределению с математическим ожиданием

a = M [ψкр ] =

1 n1 (n1 + n2 +1) и

1

2

дисперсией σ 2

= D[ψкр ] =

n1n2 (n1 + n2 ). #

12

Для принятия решения об однородности двух выборок по критерию Вилкоксона−Манна−Уитни необходимо выполнить следующие действия.

1) Проанализировать объемы выборок n1 и n2 , сравнить их между собой. Меньшую выборку будем считать первой. Пусть n1 − объем меньшей выборки.

2) Из двух выборок составляем общий вариационный ряд с обозначением рангов вариант. Если в обеих выборках есть одинаковые варианты, то в общем вариационном ряду первыми записываются варианты меньшей (первой) выборки.

129

4-й шаг. По статистическим таблицам критических точек распределения Вилкоксона−Манна−Уитни для уровня значимости а находим нижнюю

критическую точку ψкр.н = ωα (n1 , n2 ) , где ωα (n1 ,n2 ) − квантиль распределения

		2	2
Вилкоксона−Манна−Уитни.
Верхняя критическая точка находится из выражения
ψкр.в = (n1 + n2 +1)n1 −ψкр.н						(9.5)
или в	виде	ψкр.в = 2MW −ψкр.н , где	2MW	находится из таблицы для
соответствующих n1 и n2.			значения		критической статистики
5-й	шаг.	Вычисление расчетного
n1+n2
ψ расч =	∑Ri(1)	осуществляется суммированием		рангов Ri(1) вариант		первой
	i=1
выборки в		общем вариационном	ряду.	Если	выполняется	условие

ψкр.н ≤ψ расч ≤ψкр.в , то гипотеза H0 верна, в противном случае H0 отвергается.

Случай Б. Объем хотя бы одной из выборок больше 25. Отличие данного случая от предыдущего состоит только в вычислении ψкр.н на четвертом шаге:

= ωα (n1, n2 ) =

(n

+ n

2

+1)n

−1

− u

n n

(n

+ n

+1)

ψкр.н

1

1

α

1

2

1

2

,

(9.6)

2

2

1−

2

12

где

u

α

− квантиль

нормального

распределения

уровня

1 −α / 2 ,

которая

1−

2

находится по статистическим таблицам нормального распределения.

u

α

u

α

1

−

α

Замечание 9.7.

можно также находить в виде

= arg Φ

2

, где

1−

2

1−

2

Φ( ) − функция Лапласа, табличные значения которой известны.

Пример 9.5. Объемы дневных продаж овощных магазинов в двух районах области представлены выборками (табл. 9.7, 9.8) xi, yi, i =1,27 (в тыс. руб.).

Таблица 9.7

X:	17	13	22	9	20	9	20	9	22
	20	21	21	22	19	23	14	20	19
	17	11	8	21	10	20	18	11	15
							Таблица 9.8
Y:	17	13	22	9	20	10	16	9	21
	15	21	21	22	18	21	15	20	18
	17	11	8	21	17	15	18	11	19

130