
- •Экзаменационный билет № 01
- •Экзаменационный билет № 02
- •Экзаменационный билет № 03
- •Экзаменационный билет № 04
- •Экзаменационный билет № 05
- •Экзаменационный билет № 06
- •Экзаменационный билет № 07
- •Экзаменационный билет № 08
- •Экзаменационный билет № 09
- •Экзаменационный билет № 10
- •Экзаменационный билет № 11
- •Экзаменационный билет № 12
- •Экзаменационный билет № 13
- •Экзаменационный билет № 14
- •Экзаменационный билет № 15
- •Экзаменационный билет № 16
- •Экзаменационный билет № 17
- •Экзаменационный билет № 18
- •Экзаменационный билет № 19
- •Экзаменационный билет № 20
Экзаменационный билет № 20
1. Классификация уравнений с частными производными 2-го порядка. Приведение уравнений с постоянными коэффициентами к каноническому виду.
2. Неравенство Чебышёва (с доказательством).
3.
Найти потенциал в центре квадрата со
стороной
 ,
если на трёх сторонах квадрата потенциал
равен нулю, а на четвертой стороне
задается формулой
,
если на трёх сторонах квадрата потенциал
равен нулю, а на четвертой стороне
задается формулой
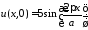 .
.
4.
Масса пойманной рыбы подчинена нормальному
закону с параметрами
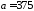 г,
г,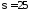 г. Найти вероятность того, что масса
пойманной рыбы будет от 300 г до 425 г.
г. Найти вероятность того, что масса
пойманной рыбы будет от 300 г до 425 г.
1. Для уравнения второго порядка от двух независимых переменных
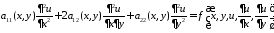
принята такая классификация:
-
если в некоторой области
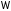
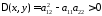 ,
то уравнение называется гиперболическим
в
,
то уравнение называется гиперболическим
в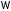 ;
;
-
если
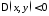 в области
в области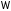 ,
то уравнение называется эллиптическим
в
,
то уравнение называется эллиптическим
в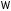 ;
;
-
если
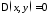 во всех точках области
во всех точках области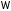 ,
то уравнение называется параболическим
в
,
то уравнение называется параболическим
в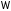 .
.
В каждом классе уравнений есть простейшие уравнения, которые называются каноническими.
Уравнения
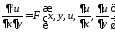 ,
,
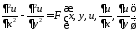
называют соответственно первой и второй каноническими формами гиперболического уравнения.
Уравнение
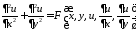
называется канонической формой эллиптического уравнения.
Уравнение
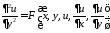
называется канонической формой параболического уравнения.
Дифференциальные уравнения
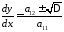
или
 (если
(если
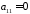 )
)
называются дифференциальными уравнениями характеристик.
Если в уравнении постоянные коэффициенты, т.е. для уравнения
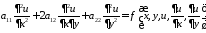 ,
,
решением уравнений характеристик есть

Если
уравнение гиперболического типа (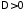 ),
то с помощью замены переменных
),
то с помощью замены переменных
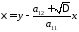 ,
,
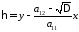
уравнение сводится к первой канонической форме.
Для
уравнения эллиптического типа (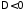 )
к канонической форме сводит замена
)
к канонической форме сводит замена
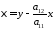 ,
,
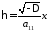 .
.
Для
уравнения параболического типа (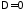 )
к канонической форме сводит замена
)
к канонической форме сводит замена
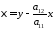 ,
,
 .
.
2.
Для любой случайной величины
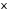 и любого положительного числа
и любого положительного числа справедливо неравенство Чебышева
справедливо неравенство Чебышева
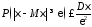 .
.
Доказательство
проведем для случая, когда
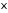 – непрерывная случайная величина. Пусть
– непрерывная случайная величина. Пусть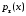 – плотность случайной величины
– плотность случайной величины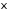 ,
а
,
а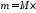 ,
тогда
,
тогда
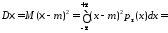
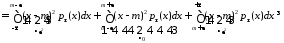
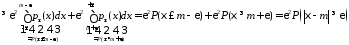 ,
,
так
как события
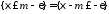 и
и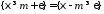 несовместны.
несовместны.
Итак,
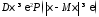 ,
,
то есть
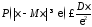 .
.
Неравенство Чебышева доказано.
Для дискретных случайных величин неравенство Чебышева доказывается аналогично (вместо интегралов будут суммы рядов).
Следствие.
Поскольку
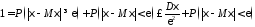 ,
то
,
то
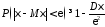 .
.
3.
Если
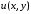 – искомый потенциал, то он является
решением задачи
– искомый потенциал, то он является
решением задачи
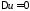 при
при
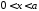 ,
,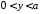 ,
,
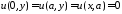 ,
,
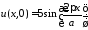 .
.
Для
решения краевой задачи воспользуемся
методом Фурье. Нетривиальные решения
уравнения Лапласа
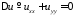 будем искать в виде
будем искать в виде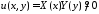 .
Подставляем в уравнение и разделяем
переменные:
.
Подставляем в уравнение и разделяем
переменные:
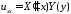 ,
,
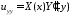 ,
,
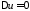 :
:
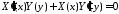 ,
,
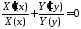 ,
,
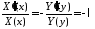 ,
,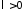 .
.
Тогда
функции
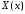 и
и являются соответственно решениями
уравнений
являются соответственно решениями
уравнений
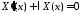 ,
,
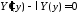 .
.
Из
краевых условий
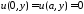 получаем краевые условия для функции
получаем краевые условия для функции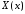 :
: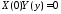 ,
,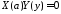 ,
значит,
,
значит,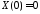 ,
,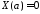 .
Таким образом, для определения
.
Таким образом, для определения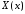 и
и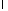 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
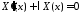
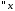 :
:
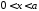 ,
,
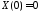 ,
,
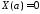 .
.
Поскольку
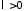 ,
то общее решение уравнения
,
то общее решение уравнения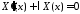 имеет вид
имеет вид
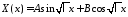 .
.
Из
краевого условия
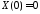 получаем:
получаем: ,
т.е.
,
т.е.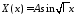 .
Из краевого условия
.
Из краевого условия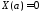 получаем:
получаем: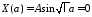 .
Поскольку
.
Поскольку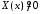 ,
то
,
то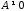 и равенство
и равенство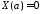 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда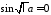 ,
откуда получаем
,
откуда получаем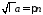 ,
,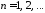 ,
т.е.
,
т.е.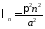 ,
,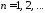 .
Тогда получим
.
Тогда получим ,
,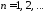 .
Таким образом, получили решение задачи
Штурма-Лиувилля:
.
Таким образом, получили решение задачи
Штурма-Лиувилля:
Собственные
значения
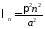 ,
,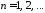 ;
;
Собственные
функции
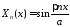 ,
,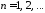 .
.
Теперь
при каждом
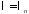 решаем уравнение для
решаем уравнение для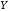 :
:
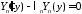
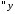 :
:
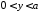 ,
,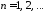 .
.
Общее решение этого уравнения имеет вид
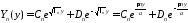 .
.
Тогда
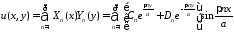 .
.
Краевые
условия
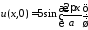 ,
,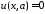 дают:
дают:
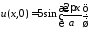 :
:
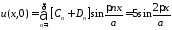
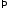
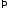
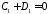 ;
;
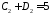 ;
;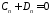 ,
, ;
;
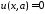 :
:
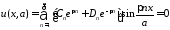
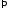
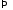
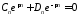 ,
,
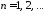 .
.
Итак,
для определения
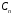 ,
,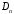 ,
,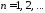 ,
получили системы
,
получили системы
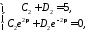
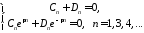
Решая их, получим
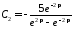 ,
,
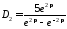 ,
,
 ,
,
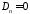 ,
,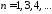 .
.
Тогда
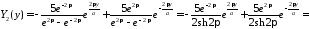
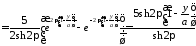 ,
,
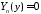 ,
,
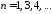 .
.
Окончательно, потенциал равен
 .
.
Значение
потенциала в центре квадрата со стороной
 ,
т.е. в точке
,
т.е. в точке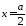 ,
,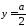 ,
равно
,
равно
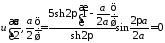 .
.
4.
Для расчета вероятностей попадания
нормальной случайной величины
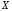 с математическим ожиданием
с математическим ожиданием и среднеквадратическим отклонением
и среднеквадратическим отклонением в промежуток
в промежуток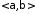 используется формула
используется формула
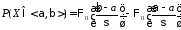 ,
,
где
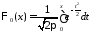 ,
причем
,
причем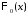 – нечетная функция:
– нечетная функция: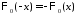 .
.
Пусть
случайная величина
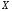 – масса пойманной рыбы. При
– масса пойманной рыбы. При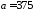 г,
г,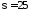 г получим
г получим
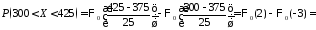
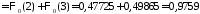 .
.
