
- •Раздел II. Дифференциальное исчисление функции одной переменной и неопределенный интеграл
- •§ 1Скорость
- •§ 2 Дифференцируемость и производная
- •Непрерывность дифференцируемой функции
- •§ 3 Понятие касательной. Касательная к графику дифференцируемой функции
- •1.Производная степной функции
- •Глава 2. Дифференциал
- •Глава 3. Основные свойства дифференцируемых функций и их применения
- •I. Рскрытие неопределенности вида
- •2.Раскрытие неопределенности вида
Непрерывность дифференцируемой функции
Установим
связь между свойствами непрерывности
и дифференцируемости функции в данной
точке ![]() .
.
Теорема. Если функция в данной точке дифференцируема, то она в этой точке непрерывна.
Доказательство.
Пусть функция ![]() дифференцируема в точке
дифференцируема в точке ![]() .
Тогда ее приращение представимо в виде
.
Тогда ее приращение представимо в виде
![]() .
.
Но
тогда при ![]() будет
будет ![]() ,
а это означает непрерывность функции
,
а это означает непрерывность функции
![]() в точке
в точке ![]() .
.
Итак,
непрерывность в данной точке является
необходимым условием для дифференцируемости.
Однако достаточным условием она не
является. Действительно, рассмотрим в
качестве примера функцию ![]() в точке
в точке ![]() .
Для нее
.
Для нее
![]()
и
предела в точке ![]() нет, а потому нет производной и нет
дифференцируемости, но
нет, а потому нет производной и нет
дифференцируемости, но ![]() ,
что означает непрерывность.
,
что означает непрерывность.
Укажем еще один пример функции
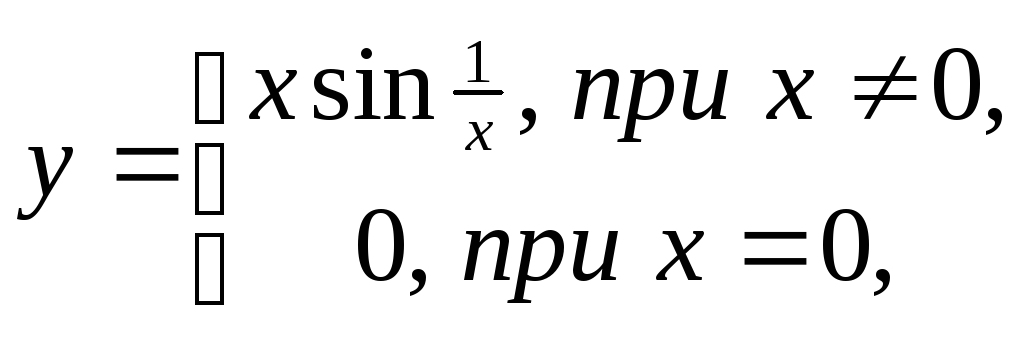
которая
в точке ![]() непрерывна (так как
непрерывна (так как![]() ),
но не дифференцируема (так как
),
но не дифференцируема (так как ![]() не
имеет предела в точке
не
имеет предела в точке ![]() ).
).
§ 3 Понятие касательной. Касательная к графику дифференцируемой функции
Из предыдущих разделов математики студентам известны различные плоские кривые (например, кривые второго порядка: окружности, эллипсы, гиперболы, параболы, а также графики различных непрерывных функций). Важным является понятие касательной прямой к таким кривым. Приведем описание этого понятия.
Пусть
L
одна из таких плоских кривых и А – точка
на L.
Если B
– другая точка на L,
то прямая P,
проходящая через A
и B,
называется секущей для L.
Пусть точка B
движется по L,
приближаясь к А сколь угодно близко.
Тогда секущая будет вращаться вокруг
точки А. Если при этом существует,
проходящая через А, прямая Т такая, что
угол ![]() между Р и Т будет сколь угодно мал (т.е.
Р будет стремится к положению Т), то
прямая Т называется касательной к L
в точке А. Касательная существует не
всегда. Так, у графика функции
между Р и Т будет сколь угодно мал (т.е.
Р будет стремится к положению Т), то
прямая Т называется касательной к L
в точке А. Касательная существует не
всегда. Так, у графика функции ![]() в точке
в точке ![]() касательной нет.
касательной нет.
Действительно
(см. рис.2), график состоит из двух
полупрямых ![]() и
и ![]() ,
образующих угол
,
образующих угол ![]() с вершиной в начале координат. При
с вершиной в начале координат. При ![]() секущая проходит вдоль
секущая проходит вдоль ![]() ,
а при
,
а при ![]() – вдоль
– вдоль ![]() ,
поэтому общего предельного положения
секущих нет. График
,
поэтому общего предельного положения
секущих нет. График ![]() в точке
в точке ![]() имеет и
имеет и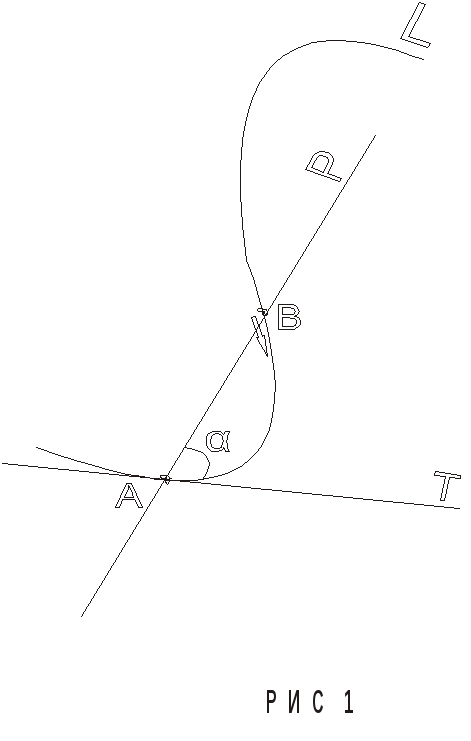 злом.
злом.
Пусть
теперь L
это график функции ![]() ,
заданной на промежутке
,
заданной на промежутке ![]() и дифференцируемой в некоторой внутренней
точке
и дифференцируемой в некоторой внутренней
точке ![]() этого промежутка.
этого промежутка.
Пусть
![]() ,
где
,
где ![]() ,
соответствующая точка графика
,
соответствующая точка графика ![]() (см. рис.3). Если
(см. рис.3). Если ![]() другая точка графика, то
другая точка графика, то ![]() и
и ![]() и секущая Р, проходящая через А и В,
наклонена к оси Ох под углом
и секущая Р, проходящая через А и В,
наклонена к оси Ох под углом ![]() .
.
Проведем
через А прямую Т, образующую с осью Ох
угол равный ![]() .
Угол между Р и Т равен
.
Угол между Р и Т равен ![]() .
Когда В приближается к А сколь угодно
близко, то
.
Когда В приближается к А сколь угодно
близко, то ![]() и, благодаря этому с учетом непрерывности
функции
и, благодаря этому с учетом непрерывности
функции ![]() :
:
![]() ,
,
то
есть ![]() .
Следовательно, Т является касательной
к графику
.
Следовательно, Т является касательной
к графику ![]() в точке А. Угловым коэффициентом
касательной Т является
в точке А. Угловым коэффициентом
касательной Т является ![]() производная функции в точке
производная функции в точке ![]() .
.
Итак, график дифференцируемой функции в соответствующей точке имеет касательную, угловой коэффициент которой равен производной в данной точке. В этом заключается геометрический смысл производной.
Видно
и обратное, если график функции в данной
точке А имеет касательную, не
перпендикулярную оси Ох, то в данной
точке ![]() существует при
существует при ![]() предел
предел ![]() (благодаря непрерывности
(благодаря непрерывности ![]() ),
функция в данной точке дифференцируема.
Ясно, что в точках разрыва касательной
быть не может. В точках же, где нет
дифференцируемости, касательная к
графику может быть, но перпендикулярная
оси Ох (см. рис 4). Значение углового
коэффициента касательной к графику
функции позволяет составить уравнение
этой касательной. Известно, что всякая
прямая (не перпендикулярная оси Ох),
проходящая через точку А(
),
функция в данной точке дифференцируема.
Ясно, что в точках разрыва касательной
быть не может. В точках же, где нет
дифференцируемости, касательная к
графику может быть, но перпендикулярная
оси Ох (см. рис 4). Значение углового
коэффициента касательной к графику
функции позволяет составить уравнение
этой касательной. Известно, что всякая
прямая (не перпендикулярная оси Ох),
проходящая через точку А(![]() ),
имеет уравнение
),
имеет уравнение ![]() .
.
Так
как для касательной ![]() , то уравнение касательной
, то уравнение касательной ![]() .
.
Прямая,
проходящая через А(![]() )
и перпендикулярная касательной,
называется нормалью к графику функции
)
и перпендикулярная касательной,
называется нормалью к графику функции
![]() .
Так как ее угловой коэффициент
.
Так как ее угловой коэффициент ![]() ,
то уравнение нормали имеет вид
,
то уравнение нормали имеет вид ![]() .
.
Например,
для кривой ![]() в точке
в точке ![]() имеет
имеет ![]() ,
поэтому уравнение касательной в точке
А(
,
поэтому уравнение касательной в точке
А(![]() )
)
![]() ,
,
а
уравнение нормали ![]() .
.
Дифференцирование суммы, произведение и частного
ТЕОРЕМА.
Если функции ![]() и
и ![]() имеют производные в данной точке
имеют производные в данной точке ![]() ,
то в этой точке имеют производные их
сумма, разность, произведение и частного
(последнее при условии
,
то в этой точке имеют производные их
сумма, разность, произведение и частного
(последнее при условии ![]() ),
причем имеют место формулы:
),
причем имеют место формулы:
![]() ;
;
![]()
![]()
Доказательство.
1. Обозначим ![]() .
Тогда
.
Тогда ![]() .
.
Отсюда
(при ![]() )
) ![]() .
.
При
![]() правая часть этого равенства имеет
предел, равный
правая часть этого равенства имеет
предел, равный ![]() ,
поэтому и левая часть имеет тот же
предел, то есть
,
поэтому и левая часть имеет тот же
предел, то есть
![]()
![]() .
.
2.
Обозначим ![]() .
.
Тогда
![]()
![]()
![]() =
=![]() .
.
Отсюда![]() .
.
Функция
![]() благодаря дифференцируемости в точке
благодаря дифференцируемости в точке![]() непрерывна в этой точке и потому
непрерывна в этой точке и потому ![]() при
при ![]() .
Следовательно, существует предел
.
Следовательно, существует предел ![]() . При этом
. При этом ![]() .
.
3.
Обозначим ![]() . Заметим, что из условия
. Заметим, что из условия![]() и непрерывности
и непрерывности ![]() в точке
в точке ![]() следует, что
следует, что ![]() в некоторой окрестности
в некоторой окрестности ![]() .
.
Имеем
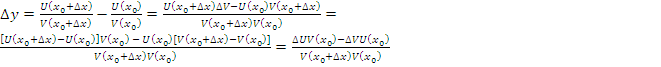 .
.
Отсюда
![]() , поэтому существует предел этого
выражения при
, поэтому существует предел этого
выражения при ![]()
![]() .
.
Теорема доказана.
Отметим два важных следствия.
Следствие
1.
Если С – постоянная, а ![]() дифференцируема в данной точке, то в
этой точке дифференцируема
дифференцируема в данной точке, то в
этой точке дифференцируема ![]() , причем
, причем ![]() ,
то есть постоянный множитель выносится
за знак производной.
,
то есть постоянный множитель выносится
за знак производной.
Действительно,
![]() ,
а производная постоянная функции равна
нулю:
,
а производная постоянная функции равна
нулю:
![]() .
.
Следствие
2.
Если ![]() дифференцируема в данной точке, то в
этой точке дифференцируема любая
натуральная степень
дифференцируема в данной точке, то в
этой точке дифференцируема любая
натуральная степень ![]() ,
причем
,
причем
![]() .
.
Действительно,
это справедливо для ![]() и
и ![]() .
Общий случай доказывается методом
математической индукции.
.
Общий случай доказывается методом
математической индукции.
Пусть
утверждение верно для ![]() .
Тогда
.
Тогда
![]() .
.
Дифференцирование сложной функции
ТЕОРЕМА.
Пусть функция ![]() имеет производную в точке
имеет производную в точке ![]() ,
а функция
,
а функция ![]() имеет производную в точке
имеет производную в точке ![]()
![]() .
Тогда сложная функция (композиция)
.
Тогда сложная функция (композиция) ![]() имеет производную в точке
имеет производную в точке ![]() ,
причем справедлива формула
,
причем справедлива формула
![]() .
.
Доказательство.
Приращению ![]() аргумента
аргумента ![]() соответствует приращение
соответствует приращение ![]() функции
функции ![]() . Приращению
. Приращению ![]() в свою очередь соответствует приращение
в свою очередь соответствует приращение
![]() функции
функции ![]() . Так как
. Так как ![]() дифференцируема в точке
дифференцируема в точке ![]() ,
то
,
то
![]() ,
,
где
![]() при
при![]() .
.
Отсюда
![]() .
.
При
![]() благодаря непрерывности
благодаря непрерывности ![]() в точке
в точке ![]() имеем
имеем ![]() и
и ![]() .
Поэтому
.
Поэтому ![]() имеет предел при
имеет предел при ![]() , и этот предел равен:
, и этот предел равен:
![]() .
.
Дифференцирование обратной функции
ТЕОРЕМА.
Пусть у функции ![]() ,
отображающей промежуток
,
отображающей промежуток ![]() в промежуток
в промежуток ![]() ,
имеется обратная функция
,
имеется обратная функция ![]() .
Пусть для
.
Пусть для ![]() соответствующая точка
соответствующая точка ![]() . Если
. Если ![]() имеет производную в точке
имеет производную в точке ![]() ,
отличную от нуля , то обратная функция
,
отличную от нуля , то обратная функция
![]() имеет производную в точке
имеет производную в точке ![]() ,
причем
,
причем
![]() .
.
Доказательство.
Придадим аргументу обратной функции
![]() в точке
в точке ![]() приращение
приращение ![]() . Этому приращению соответствует
приращение
. Этому приращению соответствует
приращение ![]() также отличное от нуля, благодаря взаимно
однозначному соответствию между
также отличное от нуля, благодаря взаимно
однозначному соответствию между![]() и
и ![]() .
Очевидно,
.
Очевидно,
![]() ;
;
если
![]() ,
то, согласно непрерывности
,
то, согласно непрерывности ![]() в точке
в точке ![]() ,
будет
,
будет ![]() .
По условию
.
По условию ![]() ,
поэтому существует предел
,
поэтому существует предел ![]() ,
то есть обратная функция имеет
производную, причем
,
то есть обратная функция имеет
производную, причем
![]() .
.
Производные основных элементарных функций
Покажем, что все основные элементарные функции дифференцируемы в любой внутренней точке их областей определения и найдем их производные. При этом используем различные замечательные пределы.
