Глава 2. Дифференциал

Дифференциал и его связь с производной

Функция , определенная на промежутке , дифференцируема в точке , если ее приращение в этой точке можно представить в виде , где от не зависит, а - бесконечно малая функция в точке . Таким образом, приращение функции представляется в виде суммы линейной относительно функции и функции , бесконечно малой более высокого порядка, чем :

при

Поэтому функцию называют главной линейной частью приращения .

Определение. Главная линейная часть приращения дифференцируемой функции в данной точке называется дифференциалом функции в данной точке.

Дифференциал функции обозначают:

Выше было показано, что дифференцируемость функции в точке равносильна существованию производной в этой точке и что . Следовательно, формула для дифференциала имеет вид

Если, в частности, взять функцию , то учитывая, что , получаем , то есть для аргумента дифференциал и приращение совпадают. Поэтому формула дифференциала принимает следующий вид

Это равенство дает возможность выразить производную через дифференциалы функции и аргумента

Пример. Для имеем .

Дифференциал функции в общем случае не равен приращению , но часто пользуются приближенным равенством

Абсолютная погрешность этого приближения равна , а относительная (при ):

Видно, что относительная погрешность может быть сколь угодно малой при достаточно малых .

Например, для функции приближенное равенство принимает вид

Поэтому.

Геометрический и механический смысл дифференциала

Рассмотрим график дифференцируемой функции (рис5.) А и В – точки графика, соответствующие значениям аргумента и , имеют ординаты и Приращение ординаты равно (по модулю) длине отрезка BD.

Если же рассмотреть касательную прямую к графику в точке A: , то на этой прямой точки А и С, соответствующие аргументам и , имеют ординаты и . Приращение ординат (равное по модулю длине отрезка СD) равно , а это дифференциал функции в точке .

Итак, дифференциал функции в точке - это приращение ординаты точки касательной прямой к графику в точке , соответствующее изменению абсциссы от до . В этом и состоит геометрический смысл дифференциала функции.

Пусть закон движения материальной точки по прямой. В некоторой момент скорость движения равна . Дифференциал функции в момент :

представляет собой путь, пройденный точкой за время с постоянной скоростью . Это составляет механический смысл дифференциала.

Дифференциал суммы, произведение и частного

Из известных формул для производных суммы, произведение и частного двух дифференцируемых функций ) и ) следуют соответствующие формулы для дифференциалов.

);

;

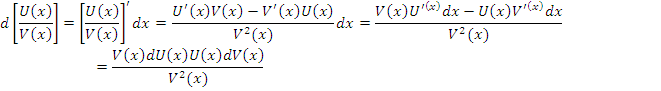
Таким образом , ;

;

В случае частного предполагается . Так как , где С – постоянная, то имеет место правило : , т.е. постоянный множитель выносится за знак дифференциала.

Дифференциал сложной функции

Пусть функция в точке , а функция дифференцируема в соответствующей точке . Тогда сложная функция , как было показано, имеет производную в точке , а потому дифференцируема.

При этом для дифференциала сложной функции имеем формулу

Инвариантная форма дифференциала

Дифференциал функции , как было показано выше, вычисляется по формуле .

Здесь - произвольное приращение аргумента (независимой переменной).

Если же имеется сложная функция , где , то дифференциал равен .

Но - дифференциал промежуточного аргумента и поэтому окончательная форма записи дифференциала

та же, что и относительно независимой переменной .

Итак, дифференциал имеет неизменную (инвариантную) форму относительно аргумента. Следует однако отметить, что в общем случае .

Из инвариантности формы дифференциала следует, что при любом выборе аргумента производная равна отношению дифференциалов: . Поэтому правило дифференцирования сложных функций записывается следующим образом

а правило дифференцирования обратных функций

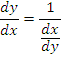
Дифференциалы высших порядков

Дифференциал функции зависит как от аргумента , так и от его дифференциала (от последнего линейно). Если зафиксировать , то дифференциал становится функцией лишь .

Второй дифференциал (дифференциал второго порядка) функции определятся как дифференциал от дифференциала и обозначается , при условии, что фиксировано.

Дифференциалы любых порядков определяются по индукции. Дифференциал порядка n(n-1) определяется как дифференциал от дифференциала порядка “n-1” .

при условии, что фиксировано.

Найдем формулу для дифференциала любого порядка в случае, когда - независимая переменная

,

.

Методом математической индукции выводится, что

Из последней формулы можно производную порядка n выразить через дифференциалы:

(в числителе дифференциал порядка n функции, а в знаменателе n - ая степень дифференциала аргумента).

Пусть теперь , а . Запишем второй дифференциал через промежуточный аргумент .

По правилу дифференцирования сложной функции имеем

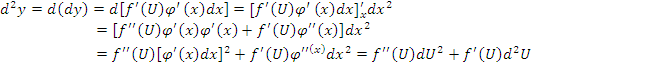
Еще более сложная формула для третьего дифференциала

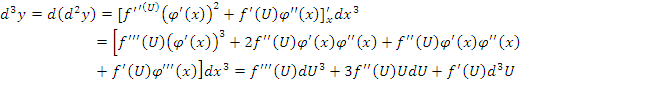
Видно, что дифференциалы второго и выше порядков инвариантностью формы не обладают.