Глава 3. Основные свойства дифференцируемых функций и их применения

Основные теоремы о дифференцируемых функциях

Важную роль в математическом анализе играют следующие основные теоремы о дифференцируемых функциях.

Теорема Ферма. Пусть функция определена на промежутке и во внутренней точке этого промежутка принимает наибольшее или наименьшее значение. Тогда если в точке существует производная, то она равна нулю: .

Доказательство. Пусть наибольшее значение функции на : , где . Рассмотрим разностное отношение . Так как , то при это отношение неотрицательно и его предел при , а при это отношение неположительно и его предел при : . Следовательно, единственно возможно .

Если наименьшее значение функции на , то рассуждения аналогичны.

Геометрический смысл теоремы ферма состоит в том, что касательная к графику функции в точке с абсциссой параллельна оси абсцисс, если - наибольшее (см. рис.6) или наименьшее значение функции на и функция в точке дифференцируема.

Теорема Ролля. Если функция непрерывна на отрезке , дифференцируема в интервале и на концах отрезка принимает равные значения : ,то внутри отрезка найдется такая точка , что .

Доказательство. Пусть и пусть - наименьшее и наибольшее значение функции на отрезке .

Очевидно, .

Если , то функция на постоянная и ее производная всюду равна нулю. Если же , то либо , либо , то есть внутри отрезка достигается или наименьшее или наибольшее значение функции на отрезке. По теореме Ферма в соответствующей точке производная равна нулю.

Теорема доказана.

Геометрически теорема Ролля означает, что при выполнении условий теоремы внутри отрезка найдется хотя бы одна точка с, которой соответствует точка на графике с касательной, параллельной оси Ох. Очевидно, таких точек может быть несколько.

Отметим, что условия теоремы Ролля существенны. При нарушении одного из них получаем ложное высказывание. Например, функция на отрезке [-1, 1] непрерывна, на концах отрезка принимает одинаковые значения |-1|=|1| , но внутри отрезка нет точки, в которой производная равнялась бы нулю, так как нет дифференцируемости всюду на интервале ]-1, 1[.

Теорема Лагранжа. Если функция непрерывна на отрезке и дифференцируема в интервале , то внутри отрезка найдется такая точка , что справедливо равенство .

Доказательство. Рассмотрим вспомогательную функцию

Легко видеть, что функция удовлетворяет всем условиям теоремы роля: она непрерывна на и дифференцируема на как сумма функций, непрерывных на и дифференцируемых на , и . Поэтому, согласно теореме Ролля, найдется такая точка , что .

Но ,

поэтому ,

откуда и следует доказываемое равенство.

Теорема Лагранжа доказана как следствие теоремы роля. Заметим, что сама теорема Ролля является частным случаем теоремы Лагранжа и получается из нее, если положить .

Выясним геометрический смысл теоремы Лагранжа. Рассмотрим график функции , заданной на и точки А и В графика с абсциссами а и b . Видно, что угловой коэффициент хорды АВ, а угловой коэффициент касательной к графику в некоторой точке С с абсциссой . Следовательно, теорема Лагранжа утверждает, что на графике функции между точками А и В найдется такая точка С, касательная в которой параллельна хорде АВ (см. рис 8).

Если в формуле Лагранжа положить , где 0< , то формула Лагранжа принимает вид

Это формула конечных приращений.

Как в случае теоремы Ролля, условия теоремы Лагранжа существенны и ,при нарушении одного из них получаем ложное высказывание.

Теорема Коши. Если каждая из функций и непрерывна на отрезке и дифференцируема в интервале , причем в , то найдется такая точка , что справедливо равенство

Доказательство. Предварительно отметим, что , так как в противном случае по теореме роля в интервале нашлась бы точка, в которой производная обращалась бы в нуль, а это противоречит условию теоремы.

Рассмотрим вспомогательную функцию

Эта функция непрерывна на и дифференцируема в как сумма функций непрерывных на и дифференцируемых в .Кроме того, . Поэтому, согласно теореме Ролля, существует точка такая , что . Но

поэтому .

Отсюда и следует доказываемая формула Коши.

Отметим, что формула Лагранжа получается из формулы Коши в частном случае при .

Теорема Дарбу. Если функция дифференцируема на некотором промежутке, то для ее производной всякое число, лежащее между двумя значениями этой производной, также является значением этой производной.

Доказательство. Пусть а и b (a<b) точки промежутка, на котором данная функция дифференцируема и пусть для определенности .Рассмотрим любое промежуточное число .

Для доказательства теоремы построим три вспомогательные функции:

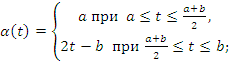
и

Видно, что и что непрерывна в интервале .Видно также, что при ,а при ,. Доопределим в точках a и b, положив ее равной ее пределам . Тогда становится непрерывной на отрезке .

согласно теореме о промежуточных значениях непрерывной на отрезке функции, существует , такое, что . Но по теореме Лагранжа найдется такое С между , что

Значит, .

Следствие. Если функция дифференцируема на некотором промежутке, то на этом промежутке может иметь разрывы только второго рода.

Например, функция

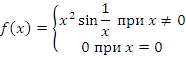
имеет всюду производную

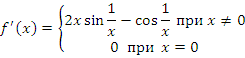
у которой в точке разрыв второго рода.

Условия постоянства функции на промежутке

Если функция на некотором промежутке постоянная, то ее производная всюду равна нулю. Справедливо и обратное утверждение.

Теорема. Если функция дифференцируема на некотором промежутке и всюду ее производная равна нулю, то функция на этом промежутке постоянная.

Доказательство. Пусть на дифференцируема и всюду . Если - некоторая фиксированная, а -любая точка , то на отрезке между выполнены условия теоремы Лагранжа. Поэтому существует между точка такая, что .

Следовательно, и потому функция постоянная на .

Возрастание и убывание функции в точке и на промежутке

При помощи производных исследуется локальное и глобальное поведение функции.

Определение. Функция называется возрастающей (убывающей )

в некоторой внутренней точке области определения, если существует окрестность , в которой при при при ).

Достаточное условие возрастания (убывания) функции в точке дает следующая теорма.

Теорема 1. Если функция дифференцируема в точке и , то эта функция в точке возрастает (убывает).

Доказательство. Пусть . Так как , то

Отсюда следует, что в - окрестности (кроме точки ) выполнены неравенства

В качестве возьмем положительное число, меньшее .

Тогда и . Это означает, что в - окрестности при и при , то есть функция возрастает в точке .

Аналогично доказательство в случае .

Заметим, что условие теоремы не является необходимым для возрастания (убывания)

функции в точке.

Например, функция возрастает в точке , а .

Перейдем к изучению монотонности функции на промежутке при помощи производных. Будем считать, что функция непрерывна на некотором промежутке и дифференцируема во всех внутренних точках. Напомним, что функция на множестве M называется строго возрастающей, если

и возрастающей или неубывающей на этом множестве, если

Аналогичны определения для строгого убывания и убывания или невозрастания.

Теорема 2. Для того чтобы на была строго возрастающей (строго убывающей), достаточно, чтобы в интервале было .

Доказательство. Для любых двух точек , на отрезке выполнены условия теоремы Лагранжа. Поэтому для некоторой точки

Если всюду в , то и функция на строго возрастает, а если , то и функция на строго убывает.

Условия теоремы не являются необходимыми. Например, функция на отрезке [-1;1] строго возрастает, но .

Теорема 3. Для того чтобы на была возрастающей или неубывающей (убывающей или невозрастающей), необходимо и достатаочно, чтобы всюду в интервале было .

Доказательство. Достаточность доказывается точно так же как в предыдущей теореме при помощи теоремы Лагранжа. При получаем , а при для , т.е. возрастание или, соответственно, убывание.

Перейдем к доказательству необходимости. Пусть любая точка интервала , а .

Если функция возрастает, то , поэтому .

Переходя к пределу при получаем .

Аналогично для убывающей функции получим .

Пример. Найти интервалы монотонности функции

Эта функция дифференцируема на промежутках , и ее производная

Видно, что в интервалах , а в интервалах ]-1, 1[ и ]1,3[. Таким образом, данная функция строго возрастает на , а на ]-1, 1[ и ]1,3[ строго убывает.

Понятие максимума и минимума

Максимальное и минимальное значение функции на некотором множестве это наибольшее и наименьшее ее значения на этом множестве. Максимум и минимум объединяются общим названием – экстремум. Наряду с глобальным понятием экстремума имеется локальное понятие экстремума.

Определение. Функция во внутренней точке области определения имеет локальный максимум (минимум) , если найдется такая окрестность точки , в которой наибольшее (наименьшее) среди значений этой функции, т.е. для всех из указанной окрестности.

Одна и та же функция может иметь несколько точек локального максимума и минимума с различными значениями функции в них (экстремальными значениями) . Так, функция, график которой изображен на рис.9 имеет локальный максимум в точках , а локальный минимум в точках . Отметим, что локальное минимальное значение может быть больше некоторого локального максимального значения.

Необходимые условия экстремума

Теорема. Если функция в точке имеет локальный экстремум, то она в этой точке либо не дифференцируема, либо имеет в этой точке производную, равную нулю: .

Доказательство. Пусть точка локального экстремума и пусть в этой точке функция дифференцируема. Так как на некотором интервале, содержащем , значение наибольшее или наименьшее среди значений, принимаемых на этом интервале, то по теореме Ферма .

Теорема имеет простой геометрический смысл: в точке графика, соответствующей точке локального экстремума, либо касательная параллельна оси Ох, либо касательной не существует, либо параллельна оси oY.

Примером функции, не дифференцируемой в точке экстремума, является , которая в точке имеет минимум и не имеет производной.

Доказанное условие экстремума является необходимым, но не является достаточным. Например, функция в точке имеет производную, равную нулю, но не имеет в этой точке экстремума.

Точки, в которых выполнено необходимое условие экстремума (точки, в которых , и точки, в которых не дифференцируема), называются критическими. Это точки “подозрительные на экстремум”. Вопрос о наличии экстремума в критических точках решается с помощью достаточных условий.

Достаточные условия максимума и минимума

Следующее достаточное условие локального экстремума использует информацию о первой производной данной функции.

Теорема 1. Пусть для функции точка является критической и пусть функция дифференцируема в некоторой окрестности , исключая может быть точку , в которой она непрерывна.

Тогда, если при переходе через производная меняет знак, то функция в точке имеет локальный экстремум. Если при этом знак меняется с + на -, то в точке имеет локальный максимум: если же знак меняет с - на +, то в точке имеет локальный минимум.

Доказательство. Рассмотрим случай, когда в данной окрестности точки производная при переходе через меняет знак с + на -. Если любая точка этой окрестности отличная от , то на отрезке между и выполнены для условия теоремы Логранжа. Поэтому , где С некоторая точка между . Так как при и при при , то всегда , то есть .Но это означает, что в точке функция имеет локальный максимум.

Аналогично рассматривается случай локального минимума.

Из доказательства теоремы видно, что если в условиях теоремы производная имеет один и тот же знак в окрестности точки , то локального экстремума в точке нет. Действительно, в этом случае имеет разные знаки при .

Доказанное достаточное условие дает первый способ исследования функции на экстремум. Схема этого способа следующая:

1. Находятся критические точки . Для этого находят первую производную и находят корни уравнения 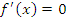. Затем находят все точки, где функция не дифференцируема.

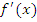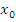2. Исследуется знак производной в окрестности каждой критической точки , т.е. для каждой критической точки 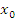достаточно малого 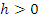определяется знак .

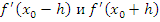3. Вывод определяется по правилу.

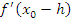
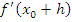
		Вывод
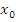+	-	- точка локального максимума
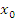-	+	- точка локального минимума
+	+	- не является точкой локального экстремума
-	-

Пример. Исследовать на экстремум функцию

Функция определена и дифференцируема на множестве .а этом множестве

Следовательно, множество критических точек этой функции есть только множество корней уравнения , то есть {-1,3}.

Для точки при малом и поэтому в точке функция имеет локальный максимум .

Для точки при малом и поэтому в точке функция имеет локальный минимум .

Рассмотрим другое достаточное условие локального экстремума, использующее вторую производную.

Теорема 2. Пусть для функции точка является критической и пусть в имеет вторую производную. Тогда, если , то функция в точке имеет локальный экстремум. Если при этом , то в имеет локальный минимум, если же , то в имеет локальный максимум.

Доказательство. Так как критическая точка и функция в имеет вторую производную (и потому имеет первую производную), то .

Пусть . Тогда имеет в положительную производную, и, следовательно, возрастает в точке . Поэтому в некоторой окрестности будет при и при . Но по предыдущей теореме тогда точка локального минимума.

Аналогично доказывается в случае .

Из доказанного достаточного условия локального экстремума вытекает второй способ исследования функции на экстремум.

Схема этого способа следующая:

1. находятся критические точки функции 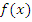, в которых 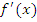, и в этих точках находится 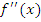(к точкам, в которых не существует первая и вторая производные, этот способ неприменим).

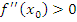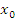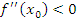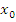2. Исследуется знак второй производной в каждой критической точке. Если , то - точка локального минимума, если , то – точка локального максимума.

Заметим, что может быть как в точках, где экстремума нет, так и в точках экстремума. Например, для функции в точке экстремума нет, хотя в этой точке , а для функции в точке минимум, но также .

Пример. Исследовать вторым способом на экстремум функцию

Эта функция на множестве имеет первую и вторую производные:

Критическими точками являются и . Так как , то в точке функция имеет локальный максимум . Так как , то в точке функция имеет локальный минимум . Отметим в заключение, что второй способ исследования на экстремум несколько проще первого, но, очевидно, имеет более узкую область применения.

Нахождение наибольших и наименьших значений

Если функция задана и непрерывна на отрезке , то по теореме Вейерштрасса, она на этом отрезке имеет среди своих значений наибольшее и наименьшее. Эти значения могут достигаться в одной из точек локального экстремума, но могут и не достигаться на одном из концов отрезка.

Поэтому для отыскания наибольшего и наименьшего значения функции на отрезке следует найти ее значения во всех точках локального экстремума, лежащих в данном отрезке, и значения на концах отрезка. Из этих значений и выбирается наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значение функции

на отрезке [-1,4].

Найдем первую и вторую производные: . Из уравнения находим критические точки . Так как , то в точке локальный максимум,. Так как , то в точке локальный минимум, .На концах отрезка функция имеет значения: . Таким образом, наибольшее значение функции 12 достигается на конце отрезка, наименьшее значение -8 достигается в точке локального минимума и на другом конце отрезка.

Задача об отыскании наибольшего и наименьшего значений функции на отрезке несколько упрощается, если на данном отрезке функция имеет единственную экстремальную точку. Это видно из следующей теоремы.

Теорема. Если функция на промежутке непрерывна и имеет единственную точку локального экстремума, то значение функции в этой точке наибольшее или наименьшее на в зависимости от того, будет ли данная точка точкой локального максимума или локального минимума.

Доказательство. Пусть в точке функция имеет локальный максимум и единственная точка локального экстремума на . Тогда в некоторой окрестности .

Предположим, что значение не является наибольшим на промежутке и что существует точка , для которой . На отрезке между благодаря непрерывности функция принимает наименьшее значение, причем это значение меньше , т.е. достигается внутри отрезка в некоторой точке . Но тогда точка является точкой локального минимума, что противоречит единственности точки локального экстремума.

Пример. Функция определена и непрерывна на промежутке и имеет на этом промежутке единственную точку локального экстремума (локального минимума) . Поэтому значение функции в этой точке наименьшее на всем промежутке.

Выпуклые функции

Пусть функция дифференцируема внутри некоторого промежутка . Тогда в каждой точке , графика существует касательная, не перпендикулярная оси Ох.

Определение 1. Говорят, что график функции в точке направлен выпуклостью вверх (вниз), если существует такая окрестность точки , что для всех точек этой окрестности точки графика лежат ниже (выше), касательной к графику функции в точке . Функция при этом называется выпуклой в точке .

Определение 2. Говорят, что график функции на промежутке направлен выпуклостью вверх (вниз) , если он направлен выпуклостью вверх (вниз) в каждой точке , где любая внутренняя точка . Функция при этом называется выпуклой на промежутке.

Например, функция выпукла на отрезке [-1,1], а ее график (см. рис. 10) направлен выпуклостью вверх на этом отрезке. Функция выпукла на , а ее график направлен выпуклостью вниз (см. рис. 11).

Установим условия того или иного направления выпуклости графика в данной точке . При этом будем полагать, что функция в точке имеет вторую производную.

Теорема. Для того чтобы график функции в точке был направлен выпуклостью вверх (вниз), необходимо условие , и достаточно условие .

Доказательство. Уравнение касательной к графику в точке имеет вид .

Поэтому взаимное расположение графика функции и касательной определяется функцией

В точке эта функция и ее производная равны нулю.

Пусть график в точке направлен выпуклостью вверх. Тогда в некоторой окрестности функция отрицательна, а потому в точке имеет максимум. Но в таком случае ее вторая производная в точке не может быть положительной. Следовательно, неравенство необходимо для направления выпуклости графика вверх в точке .

Если же , то в точке имеет максимум, т.е. в некоторой окрестности функция отрицательна. Поэтому график функции в точке направлен выпуклостью вверх.

Достаточность условия доказана.

В случае направления выпуклости графика вниз рассуждения аналогичны.

Заметим, что в точках, где , график функции может быть направлен выпуклостью либо вверх, либо вниз. Так графики функций и в точке имеют разное направление выпуклости, но в том и другом случае .

Практически для исследования выпуклости функции нужно найти ее вторую производную и определить промежутки, внутри которых и . На первых график направлен выпуклостью вверх, а на вторых – вниз.

Пример. Исследовать выпуклость функции . При имеем . Поэтому в интервале и в интервале . Следовательно, график данной функции в интервале направлен выпуклостью вверх, а в интервале - выпуклостью вниз.

Точки перегиба

Предположим, что функция дифференцируема в некоторой окрестности точки , за исключением, быть может, самой точки , в которой она непрерывна.

Определение. Точка называется точкой перегиба графика функции , если существует такая окрестность точки , что в интервале график направлен выпуклостью в одну сторону, а в - другую, т.е. при переходе через направление выпуклости графика меняется.

Теорема 1. Если в точке перегиба графика функции вторая производная функции существует и непрерывна, то она в этой точке обращается в нуль: .

Доказательство. В некоторой окрестности точки с одной стороны от выполнено неравенство , а с другой стороны, . Поэтому благодаря непрерывности второй производной в имеем .

Равенство является необходимым признаком точки перегиба, но не является достаточным. В этом можно убедится, рассматривая функцию в точке . Эта точка не является точкой перегиба, хотя в этой точке . следует иметь также ввиду, что в точке перегиба может не существовать вторая (и даже первая) производная. Например, график функции в точке имеет перегиб, но в этой точке функция не дифференцируема.

Таким образом, точки перегиба графика функции следует искать среди точек, в которых вторая производная или не существует, или равна нулю.

Укажем достаточный признак точки перегиба.

Теорема 2. Пусть функция имеет вторую производную в некоторой окрестности точки за исключением, быть может, самой точки и непрерывна в . Тогда, если в указанной окрестности имеет разные знаки слева и справа от точки , то график функции имеет перегиб в точке .

Доказательство. Так как вторая производная функции слева и справа от точки имеет разные знаки, то направление выпуклости графика функции слева и справа от точки различны. Но тогда по определению есть точка перегиба графика функции.

Из сказанного следует способ отыскания точек перегиба:

1. найти точки, в которых возможен перегиб, то есть точки, в которых 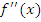либо не существует, либо обращается в нуль;

2. исследовать знак 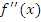в окрестности каждой такой точки и сделать вывод по схеме

Знак 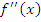при	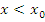Знак 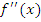при	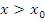Вывод
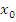+	-	- точка перегиба
-	+
+	+	не является точкой перегиба
-	-

Одновременно с исследованием точек перегиба происходит исследование направления выпуклости графика функции.

Пример. Найти точки перегиба графика функции

Данная функция имеет всюду вторую производную

Она обращается в нуль и точке .

Так как при и при , то точка является точкой перегиба, причем слева от точки график функции выпуклый вверх, а справа – вниз.

Применение дифференциального исчисления к нахождению пределов

(Правило Лопиталя)