2.1.3. Уравнения модели с полиномиально распределённым лагом (лаги Алмон)

Если в правой части уравнения (2.1) присутствует только независимая переменная со своими лаговыми значениями, то такое уравнение называется уравнением с распределённым лагом. Если максимальная величина лага ограничена (например, величиной l), то такое уравнение можно записать в виде

.

Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной x, то это изменение будет влиять на значения переменной y в течение l следующих моментов времени.

Коэффициент регрессии b₀ при переменной x_t характеризует среднее изменение y_t при изменении x_t на единицу своего измерения в некоторый фиксированный момент времени t. Этот коэффициент называют краткосрочным мультипликатором.

По аналогии с моделью (2.1) сумму всех промежуточных мультипликаторов назовём долгосрочным мультипликатором и определим как

b = b₀ + b₁ + … +b_l.

Величина b показывает изменение в долгосрочном периоде t+1 результата y под влиянием изменения на единицу независимой переменной x_t.

Введём понятие относительных коэффициентов модели с распределённым лагом

β_j = b_j/b, j = 0,1,2,…,l.

Эти коэффициенты показывают вклад отдельного лага в суммарное влияние всех лагов. Функция β_j целого аргумента называется распределением лагов. Если все коэффициенты b_j имеют одинаковые знаки, то для любого j

0 < β_j < 1 и =1.

В этом случае относительные коэффициенты β_j являются весами для соответствующих коэффициентов b_j. Каждый из них измеряет долю общего изменения результативного признака в момент времени t + j.

Зная величины β_j, можно определить такие важные характеристики модели с распределённым лагомкак величины среднего лага и медианного лага. Средний лаг определяется по формуле

и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения факторной переменной в момент времени t. Средний лаг измеряет скорость реакции y на изменение x. Небольшая его величина свидетельствует об относительно быстром реагировании результата на изменение факторной переменной, тогда как высокое его значение говорит о том, что такое воздействие будет сказываться в течение длительного периода времени.

Медианный лаг (l_Me)– это величина лага, для которого

0,5.

Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.

В общем случае оценить параметры уравнения модели с распределённым лагом методом наименьших квадратов представляется проблематичным. В этом случае оценке подлежат достаточно большое количество параметров в условиях мультиколлинеарности (лаговые переменные, как правило, тесно связаны друг с другом). Для решения этой проблемы обычно предполагаю, что известна структура лагов. Ш. Алмон (Almon S.) предложила считать, что зависимость величин коэффициентов такой модели от лагов является полиномиальной. В этом случае часть проблем, связанных с проблемами метода наименьших квадратов снимается.

Итак, будем считать, что коэффициенты модели с распределённым лагом определяются из соотношений (полином от величины лагаj степени к). Тогда после подстановки этих коэффициентов в исходное уравнение (после перегруппировки переменных) исходное уравнение можно заменить на уравнение от вспомогательных переменных с коэффициентами (эти преобразования предлагается провести самостоятельно). Вспомогательные переменные являются линейными комбинациями исходной независимой переменной и её лаговых значений с известными коэффициентами. Число вспомогательных переменных равно к (степени полинома), а поскольку это число, как правило, значительно меньше максимального лага (обычно не больше 4), то размерность вспомогательного уравнения будет существенно меньше размерности исходного уравнения. Оценив вспомогательное уравнение, определим , а затем можно рассчитать значения коэффициентов исходного уравнения по приведённой формуле.

В EViews модель распределённых лагов рассчитывается несколько по-иному, чем описывается в эконометрической литературе. Так, зависимость коэффициентов модели от лагов имеет вид

, (j = 0,1,2,…,l),

где с = .

Введено это для того, чтобы уменьшить эффект мультиколлинеарности. На конечные результаты расчётов это введение влияния не оказывает.

При использовании метода Алмон необходимо предварительно решить две проблемы: определить максимальную величину лага и степень полинома. Обе проблемы решаются эмпирически.

При решении первой проблемы рекомендуется брать как можно большую величину лага, а потом на основании статистических критериев удалять последовательно незначимые слагаемые из уравнения модели. Аналогичные рекомендации действуют и в отношении определения степени полинома. А поскольку степень полинома, как правило, бывает не больше 4, то при компьютерных расчётах это не создаёт больших затруднений. Оценка параметров модели с распределёнными лагами реализована в большинстве статистических пакетов, и исследователю остаётся просчитать ряд вариантов и выбрать из них наиболее подходящий. Рассмотрим эту процедуру на примере эконометрического пакета EViews.

Чтобы задать в EViews расчёт модели с распределённым лагом, необходимо в спецификации уравнения регрессии задать (y с pdl(x,l,k)). Здесь у – зависимая переменная, с – константа, х – независимая переменная, l – максимальный лаг, к – степень полинома, pdl – polynomial distributed lag (полиномиально распределённый лаг). На рисунке 2.1 приведён отчёт об оценке модели pdl заданной спецификацией (y с pdl(x,5,1)), т.е. приведена оценка зависимости y от x с лагом, равным пяти годам, и степенью полинома, равной единице.

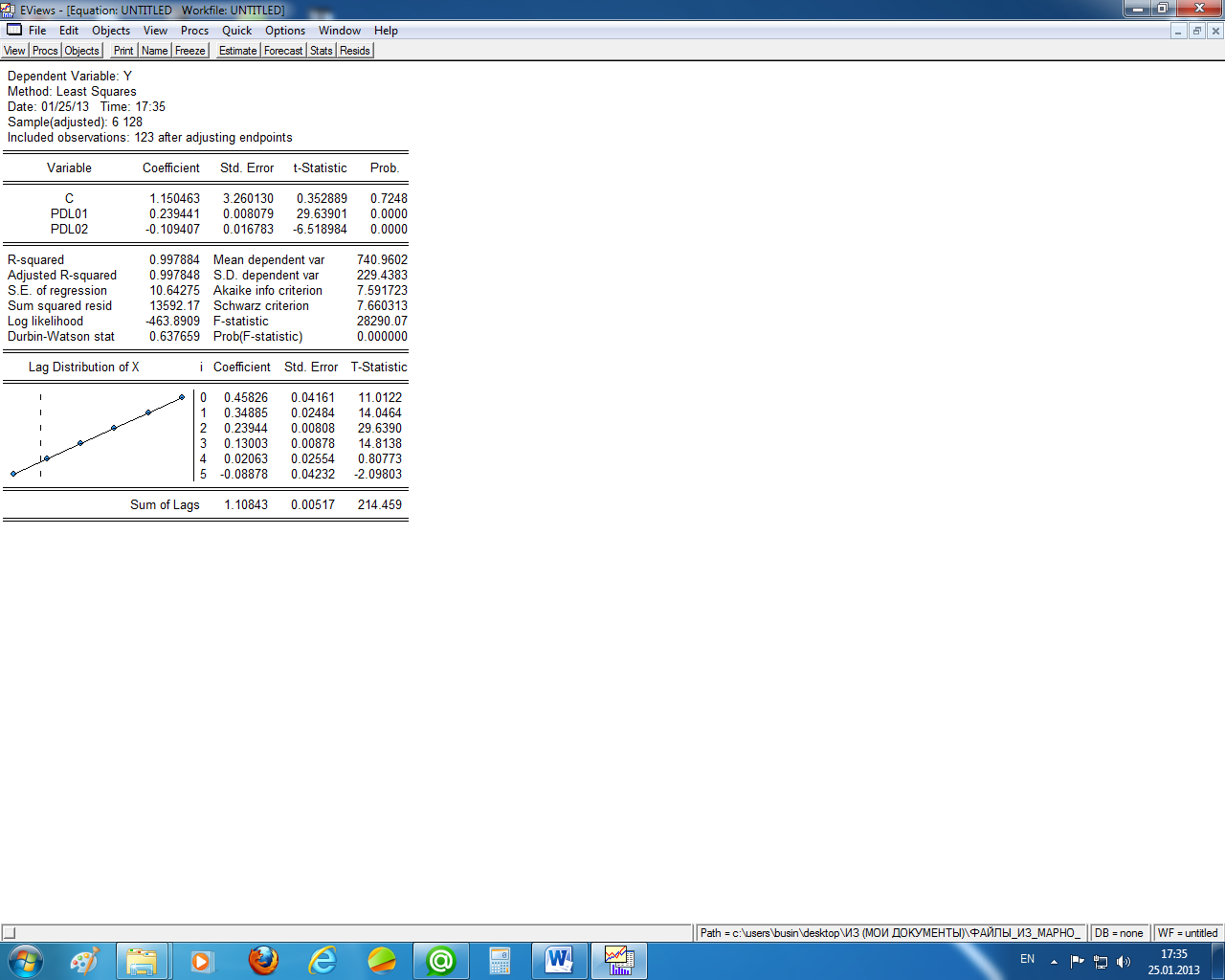
Рисунок 2.1 – Оценка параметров модели с распределённым лагом

Итак, в рассматриваемом примере уравнение с распределённым лагом в общем виде следующее:

y_t = c + b₀ x_t + b₁x_t-1 + b₂x_t-2 + b₃x_t-3 + b₄x_t-4 + b₅x_t-5 + e_t.

Коэффициенты этого уравнения рассчитываются из соотношений b_j=γ₀+γ₁(j-0,5) (полином 1-го порядка), (в нашем случае k=1 и c=k/2=0,5), а γ₀ и γ₁ определяются как оценки вспомогательного уравнения

y_t = α + γ₀ z_0t + γ₁ z_1t,

где z_0t и z_1t – вспомогательные переменные, являющиеся линейными комбинациями текущих и лаговых значений независимой переменной.

На рисунке 2.1 с – это ,PDLoj – это (j=1,2), а коэффициенты b_j (j=0,1,2.3.4.5) – это числа в последней части отчёта в столбце Coefficient. Левее их помещён график распределения лагов.

Итак, в нашем примере уравнение регрессии с распределённым лагом имеет вид (с округлениями):

y_t = 1,15 + 0,46x_t + 0,35x_t-1 + 0,24x_t-2 + 0,13x_t-3 + 0,02x_t-4 – 0,09x_t-5 + e_t.

В последней строке отчёта указан долгосрочный мультипликатор (Sum of Lags =1,11).

Отметим, что здесь найдено не лучшее уравнение регрессии. Свободный член уравнения с распределённым лагом незначим (Prob. для с равна 0,725), в остатках присутствует автокорреляция. Эти вопросы решаются отдельно и здесь не рассматриваются.