1.5. Аналитическое выравнивание временных рядов

На практике часто приходится определять функциональную зависимость уровней временного ряда от времени. С этой целью сначала необходимо выполнить выравнивание уровней временного ряда, используя одну из возможных процедур, разработанных для этих целей. После этого вид динамики просматривается более чётко.

Процесс определения зависимости уровней временного ряда как функции от времени называется аналитическим выравниванием временных рядов. Обычно такую зависимость определяют, используя обычный метод наименьших квадратов, в котором в качестве независимой переменной выступает фактор времени. При таком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.

Прогнозирование исследуемого показателя на перспективу при этом осуществляется на основе экстраполяции, т.е. на продление в будущее тенденции, наблюдавшейся в прошлом, путём подстановки в аналитически выраженную зависимость от времени значений будущих тактов времени. При этом к такой форме зависимости предъявляются все те требования, которые разработаны для классического регрессионного анализа.

Для иллюстрации применения аналитического выравнивания временного ряда рассмотрим рисунок 1.8, в котором изображены графики реального временного ряда, выравненный временной ряд по линейному тренду и график остатков уравнения тренда. Необходимо помнить, что на подобных графиках помещены две вертикальные оси координат: правая – для исходной информации, левая – для остатков.

На рисунке 1.9 приведены уравнение линейного тренда, показатели его точности и адекватности. Ясно, что данное уравнение тренда неадекватно отражает динамику временного ряда(статистика Дарбина-Уотсона близка к нулю), но пока цель определения адекватного тренда и не ставилась (здесь иллюстрируется сама идея аналитического определения уравнения тренда).

Рисунок 1.8 – Графики уравнения линейного тренда

Рисунок 1.9 – Уравнение линейного тренда

Уравнение тренда в нашем случае имеет вид (с округлениями).

y_t = 9,71 + 0,21t + e_t.

Здесь e_t – остатки, которые, как мы видим и по рисунку, и по статистике Дарбина – Уотсона, автокоррелированы (методы избавления от автокорреляции те же, что и в классическом регрессионном анализе).

Подставляя в это уравнение вместо t значения за пределами наблюдаемых значений (>50), будем получать прогнозные значения, вычисленные по тренду. При необходимости можно будет получить и интервальную оценку прогноза.

Здесь не приводится обсуждение разнообразия видов трендов, поскольку их разнообразие так велико, что только их перечень занял бы много места. При необходимости с этим можно ознакомиться в дополнительной литературе по эконометрике.

1.6. Проверка стабильности модели тренда (тест Чоу)

Идея этого теста связана с проверкой стабильности изучаемого процесса, в том числе для выявления стабильности тенденции временного ряда. Этот тест может быть реализован в двух вариантах. Один из них – Chow breakpoint test – основан на проверке гипотезы о сохранении значений всех коэффициентов модели при переходе от одного подпериода полного периода наблюдений к другому. Другой вариант теста Чоу (на качество прогноза – Chow forecast test) сравнивает качество прогноза, сделанного на основе оценивания модели на одной части периода, с качеством прогноза, сделанного на основе оценивания модели на всём периоде наблюдений.

Рассмотрим первый вариант. Допустим, что тенденция ряда имеет нестабильную тенденцию. Это значит, что, начиная с некоторого момента времени t = n₁, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику. Это означает, что момент времени n₁ сопровождается значительными изменениями ряда факторов, оказывающих воздействие на изучаемый показатель. При этом весь ряд динамики будем считать выборкой, которую можно разделить на две подвыборки: до момента n₁ и после момента n₁. При проведении теста предполагается, что на подвыборках может быть достигнута однородность информации.

Для проверки гипотезы о том, что исходная выборка однородна и разбиение её на две части не приведёт к значимому изменению оценок моделей, оценённых на подвыборках, находят параметры трёх уравнений тренда. Первое уравнение строится для всей совокупности наблюдений, второе и третье – для соответствующих выделенных подмножеств совокупности наблюдений. Для каждого из этих уравнений находят остаточную сумму квадратов SSE = Σe_i². Для общего уравнения обозначим её через SSE₀, а для уравнений по подмножествам – через SSE₁ и SSE₂ соответственно. Тогда равенство SSE₀ = SSE₁ + SSE₂ выполняется, если оценки параметров всех трёх трендов совпадают (совокупность однородная).

В противном случае SSE₀ > SSE₁ + SSE₂ и чем больше разница между разными частями этого неравенства, тем больше различие между двумя подмножествами с точки зрения значения оценок параметров уравнений трендов. Существенность различия проверяют с помощью F-критерия. Его фактическое значение находят по формуле

,

где m – число оцениваемых параметров уравнения тренда (без свободного члена), одинаковое для каждого уравнения. Если значение вычисленной статистики оказалось больше табличного (или, что всё равно, расчётный уровень значимости оказался меньше принятого), то гипотеза об однородности отклоняется и считается, что имеют место структурные сдвиги и целесообразно строить уравнение тренда для каждого подмножества в отдельности.

Рассмотренный критерий может быть применён для тестирования однородности выборки (проверки стабильности модели) при разбиении всей выборки на несколько подвыборок. В этом случае при проведении расчётов, например в EViews, надо указать точки деления выборки на подвыборки и тест проверит, есть ли существенное различие в указанных подвыборках.

Идея критерия Чоу на качества прогноза сходна с рассмотренным методом. Но есть и различия. Рассмотрим его подробнее.

Сначала оцениваются параметры модели тренда и значения уровней элементов временного ряда по всей совокупности наблюдений. Затем совокупность наблюдений разбивается на две части: по первой части оцениваются параметры модели тренда и по оценённой таким образом модели прогнозируются уровни элементов временного ряда для второй части выборки. После этого проверяется, значимо ли различаются оценённые значения уровней ряда для второй части выборки по двум моделям. Если модель стабильна, то это различие не должно быть значимым. Степень различия измеряет статистика

F = ,

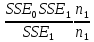где n₁ – объём первой части выборки;

SSE₀ – остаточная сумма квадратов модели, оценённой по всей выборке;

SSE₁ – остаточная сумма квадратов модели, оценённой по первой части выборки объёма n₁.

Если модель стабильна, то указанная статистика имеет распределение Фишера и гипотеза о стабильности отклоняется, если вычисленное значение этой статистики превышает табличное значение при заданном уровне значимости (или, что то же, если расчётный уровень значимости окажется меньше принятого).

Проиллюстрируем работу теста Чоу на примере проверки гипотезы об отсутствии структурных изменений в значении переменной lnGDP (поквартальные данные), уравнение линейного тренда для которой приведено на рисунке 1.10.

Рисунок 1.10 – Уравнение линейного тренда для анализируемого ряда

Особых «претензий» по качеству к уравнению тренда нет: высокий уровень коэффициента детерминации «говорит», что уравнение тренда довольно точно описывает динамику изучаемого ряда, а все его оценки значимо отличаются от нуля.

Но низкий уровень статистики Дарбина – Уотсона означает наличие высокой автокорреляции в остатках. На рисунке 1.11 изображены: график исходного ряда, линейного тренда и остатков.

Рисунок 1.11 – График анализируемого ряда, его линейного тренда и остатков

Как видно из рисунка 1.11, линейный тренд для данного ряда плохо аппроксимирует динамику этого ряда. По графику остатков видим, что где-то после 1967-го года направление динамики ряда изменилось по сравнению с линейным трендом. Проверим это по тесту Чоу (рисунок 1.12).

Рисунок 1.12 – Результаты теста Чоу на точку изменения тренда

Как видно из рисунка 1.12, расчётный уровень значимости (Probaility) меньше любого принятого уровня (обычно 0,05), следовательно, гипотеза о стабильности модели по отношению к линейному тренду отклоняется.