ДМ_Конспект

Декартовым произведением множеств X1 X 2 ... X n называется множество всех возможных упорядоченных наборов (x1 , x2 , ..., xn ) из n элементов (кортежей), в которых первый элемент (первая координата) принадлежит множеству X1 , второй (вторая координата) множеству X 2 , n -й

( n -ая	координата)		множеству		X n ,	т.е.
X1 X 2	... X n {(x1 , x2 , ..., xn ) | xi	X i , i 1,n}.
Пример.
Пусть X {a,b,c}, Y {d,e}, Z {l, m}.

Тогда

X Y Z {(a,d,l),(b,d,l),(c,d,l),(a,e,l),(b,e,l),(c,e,l),(a,d,m),(b,d,m), (c,d,m),(a,e,m),(b,d,m),(c,d,m)}.

Если X или Y , то X Y , так как не существует упорядоченных пар с отсутствующей первой или второй координатой.

Аналогично	X1 X 2 ... X n тогда и только тогда, когда хотя бы одно из
множеств X1 , X 2		,..., X n является пустым множеством.
Отдельным случаем операции декартова произведения является понятие
степени множества.
Определение.
Декартово		произведение	X X ... X , в котором			одно и	то	же
множество	X	умножается n раз само на себя,			называется декартовой
степенью множества и обозначается				X n . При этом	X 1 X .	Множество		X 2
называется	декартовым квадратом			множества	X , множество		X 3
декартовым кубом множества X .
Пример.		Пусть	X {d,e},		тогда	X 1	{d,e},

X 2 {(d,d),(d,e),(e,d),(e,e)},

X 3 {(d,d,d), (d,d,e), (d,e,d), (d,e,e), (e,e,e), (e,e,d), (e,d,d), (e,d,e)}.

Пример.

Пусть R множество действительных чисел, тогда множество R R R2множество точек на плоскости.

Определим мощность декартова произведения, используя теорему 3.1.

Теорема 3.1.

Пусть X1 , X 2 , ..., X n	конечные	множества и	| X1 | m1	, | X 2 | m2 , …,
| X n | mn . Тогда мощность	декартова	произведения	X1 X 2	... X n равна

произведению мощностей | X1 X 2 ... X n | | X1 | | X 2 | ... | X n | m1 m2 ... mn .

Доказательство теоремы можно провести методом математической индукции.

Следствие теоремы 1. Мощность декартовой степени множества X равна | X n | | X |n .

31

Пример. Пусть X {a,b,c},			Y {d,e}, Z {l, m}.
Мощность	множества	X Y Z		равна	| X Y Z | 3 2 2 12 ,	где
| X | 3 , | Y | 2 , | Z | 2 .
Мощность	множества	X 3	равна	| X 3 | | X X X | 3 3 3 27		или
| X |3 33 27.
3.2 Понятие отношений. Бинарные и n-арные отношения
Введем формальные понятия отношений.
Говорят, что (x1 , x2 , ..., xn )			находятся в		отношении R ( R является

множеством), если (x1 , x2 , ..., xn ) R .

Определение. n -арное ( n -местное) отношение R на	множествах
X1 , X 2 , ..., X n это подмножество декартова произведения этих	n множеств,

т.е. R X1 X 2 ... X n .

Определение. Унарное (одноместное) отношение R – это подмножество множества X . Такие отношения называются признаками: x обладает признаком R , если x R и R X .

Свойства унарных (одноместных) отношений – это свойства подмножеств множества X . Поэтому для случая n 1 термин «отношение» употребляется редко.

Пример.

Тернарным (трехместным) отношением являются: арифметические операции над числами; отношение между родителями и детьми (отец, мать, ребенок); множество троек нападающих в хоккейной команде.

Пропорция x : y z : u иллюстрирует четырехместное отношение.

Наиболее часто встречающимися и хорошо изученными являются бинарные, или двухместные, отношения. Эти отношения возникают между парами объектов.

Определение.

Бинарным отношением на паре множеств X и Y будем называть подмножество декартового произведения R X Y .

Пример. Отношение принадлежности (определяет связь между множеством и его элементами, обозначается ); отношение включения (определяет связь между двумя множествами); отношение равенства (=); отношение неравенства ( или ).

Примеры бинарных отношений.

1.Выражения: «быть братом», «делиться на какое-либо число»; «входить

всостав (чего-либо)».

2.Всѐ множество X Y есть отношение множеств X и Y .

32

3.

Если

A

множество

действительных

чисел,

то

{(x, y) A A | x2 y2 4}.

4.Пусть A множество товаров в магазине, а B множество действительных чисел. Тогда { x, y A B | y цена x} отношение множеств

Aи B .

5.Отношение « » выполняется для пар (7,9) и (7,7), но не выполняется для пары (9,7).

6.Если A множество людей, то {(x, y) A A | y есть родственник x}.

Для любого бинарного отношения можно записать соответствующее ему соотношение. В общем виде соотношение можно записать как xRy , где R

отношение, устанавливающее связь между элементом x из множества X (x X ) и элементом y из множества Y ( y Y ) .

Определение. Пусть | X | n , | Y | m, | X Y | n m . На паре множеств X

и Y можно построить 2nm бинарных отношений.

Определение. На множестве X , состоящем из n элементов, может быть

задано 2n2 бинарных отношений.

В дальнейшем будем рассматривать бинарные отношения, поэтому вместо термина «бинарное отношение» будем употреблять термин «отношение».

3.3 Область определения и область значений отношений

Определение.

Область определения отношения R на X и Y (обозначим DO (R) ) есть множество всех x X таких, что для некоторых y Y имеем x, y R , т.е.

область определения R есть множество первых координат упорядоченных пар из R . Область значений отношения R на X и Y (обозначим DЗ (R) ) есть

множество всех y Y таких, что x, y R для некоторого x X , т.е. область

значений есть множество всех вторых координат упорядоченных пар из R .

Пример.

В примерах отношений, приведенных выше, в частности, в (2), область определения есть все множество X , а область значений все множество Y . В

(3) как область определения, так и область значений совпадают с множеством {t | 2 t 2}. В (4) область определения есть множество A , а область значений

есть множество всех действительных чисел, каждое из которых совпадает с ценой некоторого товара в магазине. В (6) область определения и область значений есть множество всех людей, имеющих родственников.

Пример. X {2, 3} и Y {3, 4, 5, 6}. Декартово произведение этих множеств X Y {(2,3), (2,4), (2,5), (2,6), (3,3), (3,4), (3,5), (3,6)}.

33

Отношение		«быть		делителем»				есть		множество
R {(2,4),(2,6),(3,3),(3,6)}.			Отношение			«равенство		(=)» есть		множество
B {(3,3)}. Отношение « » есть пустое множество .
Области определения и значений отношения							R	это соответственно
множества DO (R) {2, 3} X и DЗ (R) {3, 4, 6} Y .
Области определения и значений отношения							B	это соответственно
множества DO (B) {3}, и DЗ (B) {3} Y .
Определение. Если x X и				y Y ,		то DO (R) X и			DЗ (R) Y . В таких
случаях R есть отношение от				X	к	Y , называется			соответствием и
обозначается X Y . Если			Y X , то		любое xRy		является подмножеством
множества X X и называется отношением в X . Если область определения
отношения совпадает с некоторым множеством X (DO (R) X ) , то говорят, что
отношение определено на X .
Существует три частных случая отношений в X :
	полное (универсальное отношение) P X X , которое имеет место
для каждой пары		x1 , x2 элементов из			X	(например, отношение «работать в

одном отделе» на множестве сотрудников данного отдела);

тождественное (диагональное) отношение, равносильное x x (например, равенство на множестве действительных чисел);

пустое отношение, которому не удовлетворяет ни одна пара элементов из X (например, отношение «быть братом» на множестве женщин).

3.4Способы задания отношений

Существует несколько способов задания отношений:

способ перечисления элементов (в виде списка);

способ задания характеристического свойства или (порождающей процедуры), выраженного в словесной или символической форме;

матричный способ;

графический способ (с помощью ориентированного графа);

с помощью фактор-множества.

Отношение полностью определяется множеством всех пар элементов (x, y) , для которых оно имеет место. Поэтому любое бинарное отношение R

можно рассматривать как множество упорядоченных пар (x, y) и задавать его в виде списка этих пар (x, y) .

Пример. На множествах чисел X {1,2,3,4,5,6,7,8,9} и Y {24,25,26}

построим отношение «делитель» ( R ), которое состоит из упорядоченных пар вида (x, y) , где x делитель y , x X , y Y :

R {(1, 24), (1, 25), (1, 26), (2, 24), (2, 26), (3, 24), (4, 24), (5, 25), (6, 24), (8, 24)}.

34

Часто отношение задается при помощи характеристического свойства,

выраженного в словесной или символической форме.
Пример. Пусть A множество женщин,					B множество мужчин. Тогда
отношение R ,	заданное		при	помощи характеристического			свойства,
выраженного	в	словесной		форме,	будет	иметь		вид
R {(a,b) A B | b является мужем а}.
Пример.	Если	A	множество		действительных		чисел,	то
R {(x, y) A A | x2 y2 4}.

Матричный способ задания отношений основан на представлении отношения соответствующей ему прямоугольной таблицей (матрицей). Еѐ строки соответствуют первым координатам, а столбцы – вторым координатам. На пересечении i -ой строки и j -ого столбца ставится единица, если выполнено

соотношение xi Ryj , и нуль, если это соотношение не выполняется (нулевые

клетки можно оставлять пустыми).

Эта матрица содержит всю информацию об отношении R .

Полному отношению соответствует квадратная матрица, все клетки которой заполнены единицами, тождественному – квадратная матрица, состоящая из нулей, с главной диагональю из единиц, а пустому – квадратная нулевая матрица.

Пример. Пусть заданы X {x1 , x2 , x3 , x4 , x5 },

Y {y1 , y2 , y3 , y4 }.

Отношение

R {(x1 , y1 ),(x1 , y3 ),(x2 , y1 ),(x2 , y3 ),(x2 , y4 ),(x3 , y1 ),(x3 , y2 ),(x3 , y4 ),(x4 , y3 )(x5 , y2 ),(x5 , y4 )}

может быть представлено следующей матрицей

	y1	y2	y3	y4
x1	1		1
x2	1		1	1
x3	1	1		1
x4			1
x5		1		1

Отношения можно задавать (или изображать) с помощью ориентированного графа. Вершины графа соответствуют элементам множеств X и Y (элементы изображаются точками на плоскости), а дуга, направленная из вершины xi к y j (направленная линия, соединяющая пары точек) означает,

что xi Ry j .

Пример. Отношение из предыдущего примера представлено в виде следующего ориентированного графа (рис.3.1).

35

x1

y1

x2

y2

x3

y3

x4

y4

x5

Рисунок 3.1 – Граф отношения R

Отношение в X отображается графом с вершинами, соответствующими элементам этого множества. При этом если имеют место соотношения xi Rx j и

x j Rxi , то вершины связываются двумя противоположно направленными

дугами, которые можно условно заменять одной ненаправленной дугой. Соотношению xi Rxi соответствует петля, выходящая из xi и входящая в эту же

вершину.

Пример. Пусть X {x1 , x2 , x3 , x4 , x5 , x6 }. Отношение

R1 {(x1 , x2 ), (x1 , x5 ), (x2 , x1 ), (x2 , x3 ), (x3 , x1 ), (x3 , x4 ), (x4 , x3 ), (x4 , y5 ), (x5 , x5 ), (x6 , y2 )}

может быть представлено в виде графа на рис. 3.2.

x6

x2

x3

x1

x4

x5

Рисунок 3.2 – Граф отношения R1

Пример.

Граф полного отношения для | X | 5 представлен в следующем виде

(рис. 3.3).

x1

x5 x2

x4 x3

Рисунок 3.3 – Граф полного отношения для | X | 5

36

Пример.

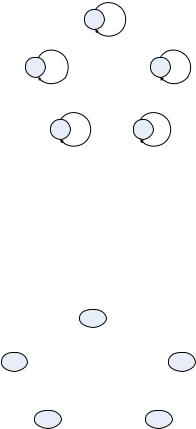
Граф тождественного отношения для | X | 5 представлен в следующем виде (рис. 3.4).

x1

x5

x2

x4 x3

Рисунок 3.4 – Граф тождественного отношения для | X | 5

Пример.
Граф пустого отношения для	| X | 5 представлен в следующем виде
(рис. 3.5).
	x1
x5	x2
x4	x3

Рисунок 3.5 – Граф пустого отношения для | X | 5

При рассмотрении способа задания отношения с помощью фактормножества введем понятие сечения отношения.

Определение

Пусть R X Y отношение на множествах X и Y . Если xi X , то сечение отношения R по элементу xi , обозначаемое R(xi ) , есть множество

R(xi ) Y ,	состоящее	из элементов	y Y	таких,	что	(xi, y) R , т.е.
R(xi ) {y Y | (xi , y) R}. Множество всех сечений отношения						R называется
фактор-множеством множества Y по отношению R и обозначают Y \ R .
Объединение сечений по элементам некоторого					подмножества Z X
называется сечением R(Z) относительно подмножества Z.
Фактор-множество полностью определяет отношение R .
Пример. Пусть заданы множества			X {a, b, c, d, e, f },			Y {1, 2, 3, 4} и
отношение	R X Y {(a,1), (a,2), (b,4), (d,1), ( f ,4)}.				Получим		сечения:
R(a) {1, 2},	R(b) {4}, R(c) , R(d ) {1}, R(e) ,				R( f ) {4}. Определим
фактор-множество		Y \ R {{1,2},{4},{1}, }.		Рассмотрим			множество
		37

D {d,e, f },

D X . Сечение отношения R по множеству D выглядит

следующим образом: R(D) R(d) R(e) R( f ) {{1}, , {4}}.

3.5 Операции над отношениями

Так как отношения – это множества, то над ними могут выполняться все теоретико-множественные операции: объединение, пересечение, дополнение и разность.

Кроме того, определяются специфические для отношений операции: сечение, обращение (симметризация) и композиция.

Рассмотрим два отношения R и S , определенные на множествах X и Y , R X Y , S X Y . В результате выполнения операций R S , R S , R \ S получаем множество упорядоченных пар, являющихся соответственно объединением, пересечением и разностью множеств R и S . Результаты выполнения этих операций также являются отношениями на множествах X и Y . Дополнение отношения R (обозначается R ) содержит все упорядоченные

пары			множества X Y ,		кроме	тех пар,	которые	принадлежат R ,		т.е.
	R {(x, y) X Y | (x, y) R}.
			Пример.	Пусть заданы		множества	X {1,2,3,4,5},		Y {a,b,c}	и
отношения				на	них	R X Y {(1,a), (1,b), (3,b), (4,c), (5,c)},
S X Y {(1,a), (2,b), (3,b), (5,a)}.
Тогда			R S {(1,a), (1,b), (2,b), (3,b), (4,c), (5,a), (5,c)};					R S {(1,a), (3,b)};
	R \ S {(1,b), (4,c), (5,c)};				S \ R {(2,b), (5,a)};

R{(1,c), (2,a), (2,b), (2,c),(3,a), (3,c),(4,a), (4,b), (5,a), (5,b)};

S{(1,b), (1,c), (2,a), (2,c),(3,a), (3,c),(4,a), (4,b), (4,c), (5,b), (5,c)}.

Пример операции сечения отношений приведен выше.

Рассмотрим операцию обращения (симметризации) отношений.

Определение

Отношение, симметричное (обратное) некоторому отношению R X Y , обозначается R 1 и представляет собой подмножество множества Y X , образованное теми парами ( y, x) Y X , для которых (x, y) R .

Если R X Y , то R 1 Y X , если R X 2 , то R 1 X 2 .

Переход от R к R 1 осуществляется взаимной перестановкой координат каждой упорядоченной пары.

Пример. Отношение R « x делитель y », а обратное к нему R 1 « y

кратно x ».

Пусть X {2, 3}, Y {3, 4, 5, 6} и A отношение «быть делителем» от X к Y . Тогда A {(2,4), (2,6), (3,3), (3,6)} и A 1 {(4,2), (6,2), (3,3), (6,3)}.

38

При переходе от R к R 1 область определения становится областью

значений и наоборот. Матрица R 1 транспонированная матрица отношения R . Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.

Рассмотрим операцию композиции отношений, которая позволяет получить отношение из двух других отношений.

Пусть даны три множества X , Y , Z и два отношения R X Y и S Y Z .

Определение

Композиция отношений R и S есть отношение C , состоящее из всех тех пар (x, z) X Z , для которых существует такое y Y , что (x, y) R и

( y, z) S .

Композиция C отношений R и S обычно обозначается как C S R (или C SR ).

Пример. Пусть заданы два отношения:

A{(x1 , y1 ),(x1 , y3 ),(x2 , y1 ),(x2 , y3 ),(x2 , y4 ),(x3 , y1 ),(x3 , y2 ),(x3 , y4 ),(x4 , y3 ),(x5 , y2 ),(x5 , y4 )}

иB {(y1 , z2 ),( y2 , z1 ),( y2 , z2 ),( y3 , z3 ),( y4 , z3 )}.

Очевидно, что композиция C B A будет представлена следующим образом

C {(x1 , z2 ),(x1 , z3 ),(x2 , z2 ),(x2 , z3 ),(x3 , z1 ),(x3 , z2 ),(x3 , z3 ),(x4 , z3 ),(x5 , z1 ),(x5 , z2 ),(x5 , z3 )}

Композиция отношений имеет следующие свойства:

S R R S , т.е. закон коммутативности не выполняется;

D (S R) (D S) R D S R , т.е. закон ассоциативности выполняется;

(S R) 1 R 1 S 1 ;

(R 1 ) 1 R .

Композиция отношений R X Y и S Y Z , где X , Y , Z множества,

наглядно представляется с помощью графов. Прежде всего, необходимо к графу отношения R достроить граф отношения S . Граф отношения C S R может быть получен при исключении вершин, соответствующих элементам множества Y . При исключении вершины yi каждый проходящий через неѐ

путь от вершин x j к вершинам zk заменяется одной дугой с тем же

направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам в C и рассматриваются как одна ветвь.

Пример. Пусть заданы множества A {a, b, c, d, e, f }, B {1, 2, 3, 4} и

C {w, x, y, z}, а также отношения R A B {(a,1), (a,2), (b,4), (d,1), ( f ,4)} и S B C {(1, x), (2, y), (3, x), (3, z)}. Построим отношение S R .

39

Построим	граф отношения R и достроим к нему граф отношения S
(рис. 3.6).
A	R		B	S	C
a
b			1		w
			2		x
c
			3		y
d
			4		z
e
f
Рисунок 3.6 Граф отношения R и отношения S
Исключим вершины yi		и каждый проходящий через неѐ путь от вершин
x j к вершинам zk	заменим одной дугой с тем же направлением, получим граф
отношения S R (рис. 3.7).
	a
	b			w
	c			x
	d			y
	e			z
	f
	Рисунок 3.7 Граф отношения S R
Аналогично	можно	получить	матрицу	композиции S R как
произведение матриц отношений S и			R (в порядке их следования), которое

выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.

3.6 Контрольные вопросы и задания

1.Как связаны между собой теория множеств и теория отношений?

2.Поясните понятие кортежа. Приведите примеры кортежей.

3.Что такое прямое (декартово) произведение множеств?

4.Как определяется мощность декартового произведения?

5.Что такое отношение множеств?

40