Raschetnye_metody_otsenki_prochnosti(1)

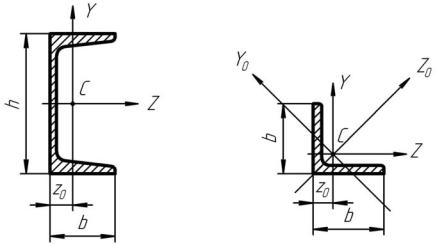
Рисунок 10 – Геометрические размеры сечений

Решение

1. Определим положение центра тяжести сложного сечения (рисунок 9). Разобьем это сечение на составляющие фигуры 1 и 2. За вспомогательные оси сечения выберем систему координат Z1 Y2. Это удоб-

но, так как в системе этих осей координаты центров тяжести элементарных фигур не будут принимать отрицательных значений. Найдем координаты центра тяжести сложного сечения по формулам:

zc

=

∑SУ 2

;

yc =

∑SZ1

,

∑A

∑A

где ∑SY 2 , ∑SZ 1 – суммарные статические моменты инерции эле-

ментарных фигур относительно вспомогатель-

ных осей Z1 Y2.

zc =

A1 z1

+ A2 z2

=

23,4 4,34 +12,3 0

= 2,84

cм;

A

+

A

23,4 +12,3

1

2

уc

=

A1 у1 + A2 у2

=

23,4 0 +12,3 7,73

= 2,66

см.

A1

+

A2

23,4 +12,3

В этом случае согласно рисунку 9:

z1 = z01 + z02

= 2,07 + 2,27 = 4,34 см;

z 2 =0;

y1 = 0;

у

2 =

h1

− y02

=

20

− 2,27 = 7,73 cм.

2

2

21

Полученные координаты центра тяжести сечения отложим от вспомогательных осей Z1 Y2 и через найденную точку проведем центральные оси Zс Yс параллельно осям Z1 Y 2 .

2. Найдем величины осевых и центробежных моментов инерции сечения относительно центральных осей Zс Yс. Для этого используем формулы перехода от центральных осей к параллельным:

J Zc = J Zc(1) + J Z(	с2) = J Z1 + A1 a12 + J Z 2 + A2 a22 ;
JYc = JYc(1) + JYc(2)	= JY 1 + A1в12 + JY 2 + A2 в22 ;
J ZcУc = J Zc(1)Уc + J Zc(2У) c		= J Z1У1 + A1 а1в1 + J Z 2У 2 + A2 a2 в2 ,	(1)
где J Zc(1) , JY(с1) , J Zc(1)Уc , J Zc(2) , JY(с2) , J Zc(2У) c		−осевые и центробежные моменты
		инерции элементарных фигур от-

носительно центральных осей всей сложной фигуры;

J Z1 , JУ1 , J Z 2 , JУ2 – осевые моменты инерции этих же фигур отно-

сительно собственных центральных осей. Эти величины находятся по таблицам сортамента прокатных профилей [1, 2, 3, 4];

a1 , в1 , a2 , в2 −координаты центров тяжести швеллера и уголка

относительно центральных осей всего сечения;

J Z1У1, J Z 2У 2 – центробежные моменты инерции швеллера и уголка относительно собственных центральных осей.

Как видно из рисунка 9,

а1 = −уc = −2,66 см;

в1 = z1 − zc	= 4,34 − 2,84 =1,5 см;
a2 = у2 − уc	= 7,73 − 2,66 = 5,07 см;

в2 = −zc = −2,84 см.

Поскольку оси Z1 Y1 являются главными осями сечения швеллера,

то J Z1У1 = 0 .

Для определения знака J X 2У 2 уголка пользуемся правилом: если зев

уголка с его центром тяжести располагается в 1 или 3 квадрантах координатных осей, центробежный момент инерции принимается отрицательным, если в 2 или 4 квадрантах – положительным. В нашем случае зев уголка расположен в 3 квадранте, значит

J X 2У2 = −42,85 см4 .

22

Подставив численные значения в формулы (1), получим:

J Zc	=1520 + 23,4(− 2,66)2 + 73,4 +12,3(5,07)2 =2075 см4;
JУС	=113 + 23,4(1,5)2 + 73,4 +12,3(−2,84)2 = 338,2 см4;

JУсZc = 0 + 23.4 (− 2.66) 1,5 − 42,85 +12,3 5,07(− 2,84)== – 313,3 см4.

3. Определим направление главных центральных осей V и U. Их угол наклона к осям Zc и Yс найдем по формуле:

	tg2α =	2J ZcYc	=	2(− 313,3)	= 0,36.
		JYc − J Zc		338,2 − 2075

Тогда 2α = 20,4˚; α =10,2˚.

Поворачивая оси Ζс и Yс против часовой стрелки (при положительном значении угла α) на угол α = 10,2˚, получаем положение главных центральных осей (рисунок 9).

4. Найдем величины моментов инерции относительно главных центральных осей по формуле:

J max =

J Zc

+ JYc

±

1

(J Zc − JУс )2 + 4J 2ZcУc .

2

min

2

Подставив числовые значения, получим:

J max

= JV

=

2075 + 338,2

+

1

(2075 − 338,2)2

+ 4 313,32

= 2130 cм4 ;

2

2

J min

= JU

=

2075 + 338,2

−

1

(2075 − 338,2)2

+ 4 313,32

= 283 cм4 .

2

2

Ось максимума (V) наклонена под меньшим углом к той из центральных осей, относительно которой центральный момент инерции сечения больше. В нашем случае

J Zc = 2075 см4 > JYc = 338,2 см4 ,

значит угол α получается между осями Zc и V. Выполним проверку по равенству

J и + J v = J Zc + JУс ,

2130 + 283 ≈ 2075 + 338,2 .

Следовательно, задача решена верно.

23

Вопросы к защите РГР № 2

1. Что такое S x , J x , J p , J xy и их единицы измерения?

2.Чему равен статический момент сечения относительно оси, проходящей через центр его тяжести?

3.Как определяются координаты центра тяжести сложного сече-

ния?

4.Как записываются формулы перехода для моментов инерции при параллельном переносе осей?

5.Чему равна сумма осевых моментов инерции сечения относительно двух взаимоперпендикулярных осей?

5.Формулы для определения осевых моментов инерции относительно центральных осей круга, прямоугольника, кольца?

7.Чему равны полярные моменты инерции круга и кольца относительно их центров?

6.Если в плоскости сечения несколько параллельных осей, относительно какой из них J x равен минимальному значению?

7.Изменяется ли сумма осевых моментов инерции относительно двух взаимоперпендикулярных осей при их повороте?

8.Как отражается на знаке центробежного момента инерции сечения расположение уголка по квадрантам координатных осей?

8.Что такое главные моменты инерции?

9.Какие оси называются главными и главными центральными осями инерции?

10.Чему равен J xy относительно главных осей инерции?

11.В каких случаях без вычисления можно установить положение главных осей инерции сечения?

12.Если J x = J y и J xy = 0 , токакие осисечения являются главными?

РГР № 3 – Внутренние усилия при изгибе стержней

Задание. Построить эпюры внутренних поперечных сил и изгибающих моментов.

Задача 1. Для заданных двух схем балок (рисунок 11) требуется написать выражения для поперечных сил Q и изгибающих моментов M для каждого участка в общем виде, построить эпюры Q и M.

Исходные данные приведены в таблице 3.

24

Рисунок 11 – Схемы балок

25

Рисунок 11 – Схемы балок

26

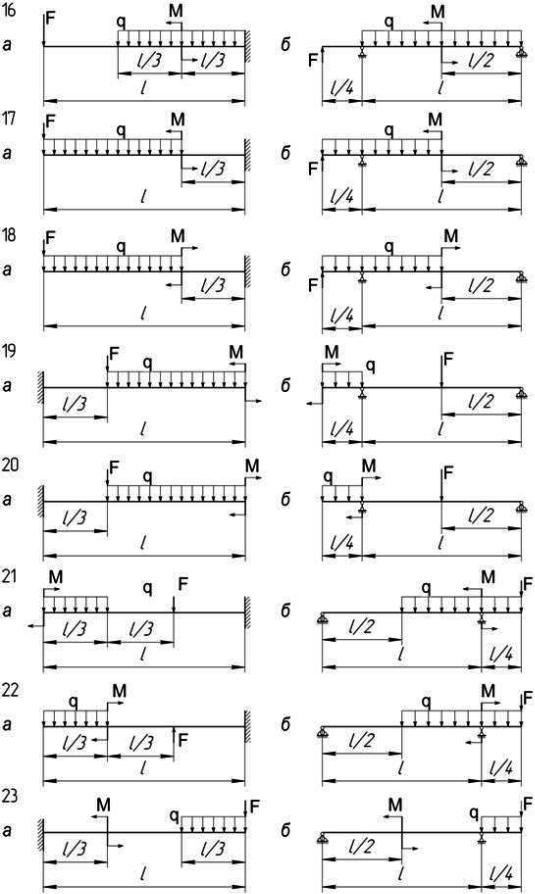
Рисунок 11 – Схемы балок

27

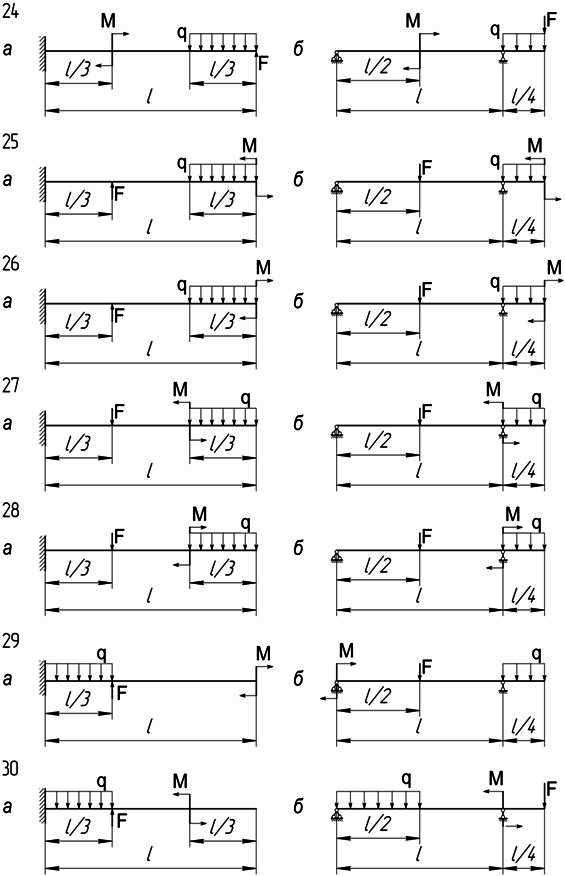
Рисунок 11 – Схемы балок

28

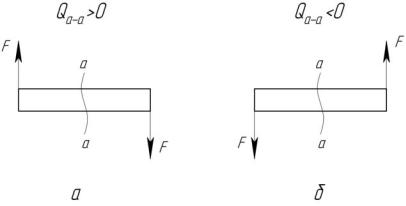
Таблица3 – Исходные данные к задаче 1

Вариант	l, м	M, кНм	F, кН	q, кН/м
1	4	10	20	4
2	6	12	22	5
3	8	14	24	6
4	8	16	26	8
5	9	16	18	4
6	6	12	16	6
7	8	14	16	8
8	4	8	14	4
9	3	10	24	2
10	9	8	26	8

Чтобы построить эпюры (графики) Q и М, надо помнить, что поперечная сила в любом сечении есть алгебраическая сумма проекций всех внешних сил, действующих по одну сторону сечения на ось, перпендикулярную оси балки. Поперечная сила Q считается положительной, если внешняя сила слева от сечения направлена снизу вверх, а справа – сверху вниз (рисунок 12 а), и отрицательна – в противоположном случае (рисунок 12 б).

Рисунок 12 – Схемы к определению знаков поперечной силы

Изгибающий момент в любом сечении определяется как алгебраическая сумма моментов всех внешних сил, действующих по одну сторону от этого сечения. Изгибающий момент считается положительным от тех нагрузок, момент которых изгибает горизонтальную балку выпуклостью вниз (рисунок 13 а), и отрицательным в случае изгиба балки выпуклостью вверх (рисунок 13 б).

29

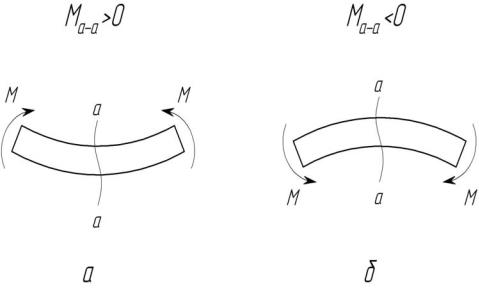
Рисунок 13 – Схемы к определению знаков изгибающих моментов

Для построения эпюр Q и М необходимо разбить балку на грузовые участки. Граница участка – это место приложения сосредоточенной внешней нагрузки или начало (конец) распределенной нагрузки.

Эпюра изгибающих моментов изображается на растянутых волокнах балки (на стороне ее выпуклости), а так как положительный момент соответствует направлению выпуклостью вниз, то положительный момент откладывается вниз, а отрицательный – вверх.

Для проверки правильности построения эпюр необходимо помнить, что в сечении, в котором к балке приложена сосредоточенная внешняя сила, перпендикулярная оси балки (в том числе и опорная реакция в виде сосредоточенной силы), значение поперечной силы Q изменяется скачкообразно на величину приложенной силы. Аналогично, в сечении, в котором к балке приложен сосредоточенный изгибающий момент (в том числе и опорная реакция в виде сосредоточенного момента), значение изгибающего момента М изменяется скачкообразно на величину приложенного момента.

На участке балки, на котором поперечная сила имеет постоянное значение, эпюра изгибающих моментов М будет ограничена прямой наклонной линией.

Изгибающий момент достигает максимума или минимума в тех сечениях балки, в которых поперечная сила равна нулю.

На участках балки, на которых распределенная нагрузка q отсутствует, поперечные силы Q постоянны, а изгибающие моменты М меняются по линейному закону.

30