
- •7. Дисперсионный анализ
- •7.1 Основные понятия
- •7.2 Однофакторный дисперсионный анализ
- •7.2.1. Теория однофакторного дисперсионного анализа
- •7.2.2. Планирование эксперимента при однофакторном дисперсионном анализе.
- •7.3 Двухфакторный дисперсионный анализ
- •7.3.1. Общие теоретические соображения
- •7.3.2. Планирование эксперимента при двухфакторном дисперсионном анализе
- •7.3 Трёхфакторный дисперсионный анализ
- •7.3.1 Общие теоретические соображения
- •7.3.3. Планирование эксперимента при трёхфакторном дисперсионном анализе
- •7.4. Многофакторный дисперсионный анализ
- •7.4.1. Общие теоретические соображения
7.2 Однофакторный дисперсионный анализ
С представленными выше воспоминаниями из математической статистики обратимся к теории неизбежного при дисперсионном анализе эксперимента. Для более выпуклого представления («для ясности») теоретических обоснований методики его проведенияпредельно упростимситуацию. В учебных целях предполагаем, что отклик У –один и зависит он отодного-единственногофактора А. Реально таких ситуаций почти не бывает, но упрощение ситуации облегчает усвоение основных принципов построения рабочих методик. А это создаёт надёжную теоретическую базу для усвоения болеесложных реальныхметодик.
7.2.1. Теория однофакторного дисперсионного анализа
При сформулированном выше допущении наш «чёрный ящик» выглядит (см. рисунок) очень просто. Здравый смысл и очевидные соображения подсказывают, что для вы-
явления
влияния фактора Ана величину от-
ИССЛЕДУЕМАЯ
СИСТЕМА клика следует несколько
раз(например,nраз)
измерить этот отклик при разных уровнях
Фактор А
Отклик У фактора А
(например, приа1,
а2,..
аi,...,аn),
получив при этом
n
штук (y1,y2,
…..yi…
,yn),
Рис. 7.3по всей видимости,разныхзначений отклика.
Очевидно,
что каждое yiиз этих значений будет определяться
реальным средним значениемY(n)Ср=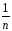
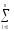 yiи прибавкой к нему ± Δyi,
обусловленной влиянием (если такое
влияние имеет место) фактораАна данном (аi)
уровне, и ошибкой ±έип
измерительного прибора.
yiи прибавкой к нему ± Δyi,
обусловленной влиянием (если такое
влияние имеет место) фактораАна данном (аi)
уровне, и ошибкой ±έип
измерительного прибора.
Фиксируем этот факт математически: yi =YСр± Δyi ±έ ип.
Далее Y(n)Ср будем обозначать символомYn, аέ ип– символом έn
Соотношение yi =Yn± Δyi ±έn равносильно(yi – Yn)= ± Δyi±έn и говорит о том, что дисперсияσ2 Генеральной совокупности слагается из двух составляющих:
- σέ2 – дисперсии, обусловленной неточностью измеренийέnи
- σА2– дисперсии, обусловленной возможным влиянием фактораА.
Аддитивность дисперсии позволяет записать: σ2 =σА2+ σέ2 илиσА2=σ2– σέ2.
На базе множества (yi –Yn), гдеi = 1,2,3… n,
можно сформировать упомянутую выше исправленную выборочную дисперсию
sи2
=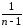 [
[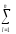 (yi)2
–
(yi)2
– (
(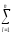 yi)2],
которая является оценкой дисперсииσ2
Генеральной совокупности
реальных значений отклика (sи2
~σ2),
ибоσn2
≡ σ2).
Но это –смешанзная оценка
(sи2
~
σА2+
σέ2)
потому, что в ней обе составляющиене
разделены. Разделить составляющие
этой смешанной оценки, ограничившись
только этимиn
измерениями,невозможно.
Предварительно следовало бы найтиотдельнооценкуs2иέдля дисперсии
σέ2и только потом можно искатьσА2
простым вычитанием:s2
–s2иέ.
~
σА2
yi)2],
которая является оценкой дисперсииσ2
Генеральной совокупности
реальных значений отклика (sи2
~σ2),
ибоσn2
≡ σ2).
Но это –смешанзная оценка
(sи2
~
σА2+
σέ2)
потому, что в ней обе составляющиене
разделены. Разделить составляющие
этой смешанной оценки, ограничившись
только этимиn
измерениями,невозможно.
Предварительно следовало бы найтиотдельнооценкуs2иέдля дисперсии
σέ2и только потом можно искатьσА2
простым вычитанием:s2
–s2иέ.
~
σА2
Для нахождения выборочной оценки s2иέдля дисперсииσέ2 необходимо создать такую выборку{ykj}m из Генеральной совокупности{yij}, в которой разброс значений был бы обусловлентолько ошибками измерений. Это мог бы быть, например, набор{ykj}m изmзначений отклика, полученных водинаковыхусловиях эксперимента, включая ипостоянство уровняфактораА (один из столбцов:аi =аk =Const, аj=1,2,3,..,m).
Эта выборзка позволяет вычислить её (выборки) параметры
Yk=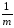
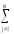 ykj
и s2иέm
=
ykj
и s2иέm
=
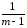
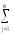 (ykj
–Ymk)2.
(ykj
–Ymk)2.
Однако, найденную на базе такой выборки по соответствующей формуле исправленную выборочную дисперсию s2иέm уженельзя вычитатьизsи2, ибо онине есть слагаемые однойоценки Генеральной дисперсии. Они– параметрыразныхвыборок. Из этого следует, что в ходе эксперимента необходимо получить ещё одну выборку{yij}q – такую, на базе которой можно вычислитьи s2иqέ,и sq2.
Реализовать это можно следующим образом.
Выполнив эксперимент, который был выше представлен первым и предполагал, что ykj =Yk± Δkj±έkj, и получивmзначений отклика, нужно проделатьэту же операциюn раз и получить nмалыхвыборок типа{yij}m, гдеj=1,2,3,..,m, и i=1,2,3,.., n.
Получившаяся
новая большая выборка{yij}q
– выборка из Генеральной совокупности
с объёмомq
= nm.
то есть для неё теперьY(nm)Ср≡
Yq=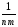
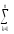
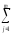 yij.
yij.
В итоге мы можем записать: σq2 =σА 2 + σέ2, где:
- σέ2– дисперсия, обусловленная инструментальной погрешностью, которая не зависит от индекса измеряемого параметра, а σq2 ≡ σ2– общая дисперсия большой Генеральной совокупности{y},выборочной оценкой для которой теперь будет
sq2
=(Σq):fq=(Σnm):fnm
=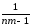 [
[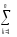
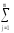 (yij)2
–
(yij)2
–
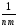 (
(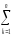
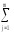 yij)2]=
yij)2]=
=
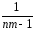 [СКq– КЧq].
где: - nm
– объёмбольшойвыборки и потому выше:
[СКq– КЧq].
где: - nm
– объёмбольшойвыборки и потому выше:
- fq =nm–1 ≡ fnm, -(Σq)= СКnm– КЧnm ≡ СКq– КЧq=(Σnm)
-
СКq=
 (yij)2≡
(yij)2≡
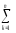
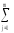 (ynm)2
=СКnm
и
(ynm)2
=СКnm
и
-
КЧq=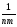 (
(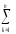
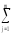 yij)2
≡
yij)2
≡
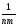 (
(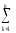
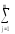 ykm)2
= КЧnm
ykm)2
= КЧnm
Общая дисперсия σ2, как и всегда, выглядит составленной из дисперсии σqип2 ≡ σέ2, которая обусловленатолько случайными факторами, и дисперсииσА2, которая обусловленатолькоизменениями уровня фактораА, то есть: σ2 =σА2 + σέ2.
Если теперь на
базе любой части{ykj)m
общей выборки{yij}q,
которая получена приодном и том жезначении фактораА,
то есть на баземалойвыборки{ykj)m
при
i=k,
вычислить исправленную выборочную
дисперсиюs2έm
=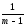
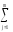 (ykj–Yk)2
, то она будет оценкой групповой исправленной дисперсиималой выборки.
(ykj–Yk)2
, то она будет оценкой групповой исправленной дисперсиималой выборки.
Таких оценок здесь будет n штук, и каждая из них будет характеризовать разброс значений отклика, обусловленныйвнутрисвоей малой выборкитолько случайнымифакторами.
Но n штук малых выборок образуют большую выборку из единой Генеральной совокупности всех возможных значений отклика. В таких случаях математическая статистикапозволяет усреднятьгрупповые оценки s2έm , а результат усредненияs2έq – рассматривать в качестве выборочной оценкиs2έqдисперсии σέq2≡ σέ2≡ σвэ2, которую ещё называют дисперсиейвоспроизводимостиэксперимента (s2έq ≡ s2вэ~ σέ2).
Итак,
s2έq
≡s2вэ
=
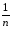
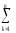 [s2έm],
а
s2έm
=
[s2έm],
а
s2έm
=
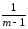 [
[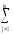 (ykj)2
–
(ykj)2
–
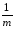 (
(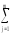 ykj)2].
ykj)2].
То
есть s2
вэ=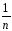
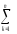
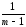 [
[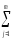 (ykj)2
–
(ykj)2
–
 (
(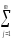 ykj)2]
=
ykj)2]
=
=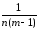 [
[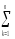
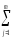 (ykj)2
–
(ykj)2
–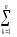
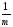 (
(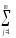 ykj)2]=
ykj)2]=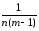 [СКq–
КЧq].
[СКq–
КЧq].
Количество степеней свободы дисперсии воспроизводимости f έв = n(m-1).
Особо подчеркнём,
что СКq
=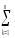
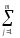 (ykj)2
=
(ykj)2
=
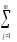 (yij)2,
а корректирующий членКЧq
“собирает” со всей выборки
средние квадраты откликов, вычисленныев каждомстолбце. В связи с этим
(в столбце факторАостаётся неизменным) иКЧqможно обозначитьКЧqА≡.
КЧА–
корректирующий член, обусловленный
фактором А.
(yij)2,
а корректирующий членКЧq
“собирает” со всей выборки
средние квадраты откликов, вычисленныев каждомстолбце. В связи с этим
(в столбце факторАостаётся неизменным) иКЧqможно обозначитьКЧqА≡.
КЧА–
корректирующий член, обусловленный
фактором А.
Действительно,
КЧq
=
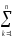
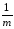 (
(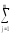 ykj)2≡
ykj)2≡
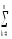
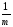 (
(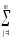 yij)2]
= КЧqА
≡.
КЧА
yij)2]
= КЧqА
≡.
КЧА
Всё это означает, что мы можем переписать выражение для выборочной оценки дисперсии воспроизводимости (повторим, что именно так в теории эксперимента часто называют дисперсию, обусловленную множеством сопровождающих эксперимент случайных факторов, включая ошибки измерений):
s2вэ
≡ s2έq
=
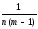 [СКq– КЧqА]=(Σ
вэ):f
вэ, где -f
вэ =n(m-1),
[СКq– КЧqА]=(Σ
вэ):f
вэ, где -f
вэ =n(m-1),
- (Σέ)q= [СКq– КЧА]
- СКq
=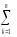
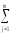 (yij)2
и
(yij)2
и
- КЧА
=
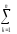
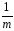 (
(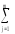 ykj)2
.
ykj)2
.
В этих условиях, в условиях однойбольшой выборки, гдеσ2 =σА 2 + σέ2,
а σέ 2 ≡σ έq, полученные выборочные оценки ужеможно комбинировать, то есть выразить:s2 – s2вэ ~ σqА2, то естьs2 – s2вэ ~ σА 2, где s2 ~ σ2, s2вэ ~ σέ2 и
s2
=
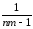 [СКq
–
КЧq]
, а
s2вэ
≡
s2έq
=
[СКq
–
КЧq]
, а
s2вэ
≡
s2έq
=
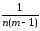 [СКq
–
КЧА].
[СКq
–
КЧА].
- s2 = sq2 = (Σq):fq = (Σ):f при (Σq)≡ (Σ) = [СК – КЧ] и fq ≡ f = nm–1;
- s2вэ≡s2έq= (Σέq):fέq = (Σέ):fέ при (Σ вэ) =[СКq – КЧq] = [СК – КЧА] и f вэ = n(m–1).
Таким образом, составляющие смешанной оценки для σ2 разделены, а
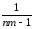 [СКq– КЧq]
–
[СКq– КЧq]
–
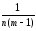 [СКq– КЧА]
~ σА
2
[СКq– КЧА]
~ σА
2
Но это ещё не вся информация, которую можно извлечь из результатов только что представленного здесь теоретически (мысленного) однофакторного эксперимента, в котором использовалась выборка объёмом q = mхn.
На базе каждой из
n
введённых в рассмотрение вышемалых выборок, кроме представленной
выше собственной групповой дисперсииs2έm,
можно вычислитьгрупповое среднеезначение отклика
Ykm
=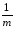
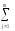 ykj.
Таких средних будетn
штук, все они будутразнымииотличающимисяот всеобщего
среднего – среднего большой выборкиYq
=
ykj.
Таких средних будетn
штук, все они будутразнымииотличающимисяот всеобщего
среднего – среднего большой выборкиYq
=
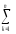
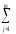 yij
. Это означает, что будут
существовать ещё иn
штук разностей типа (Ymq–Yq),
на базе которых можно вычислить
некую (ещё одну) выборочную дисперсию
yij
. Это означает, что будут
существовать ещё иn
штук разностей типа (Ymq–Yq),
на базе которых можно вычислить
некую (ещё одну) выборочную дисперсию
s2нвыб=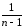
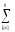 (Ymk–Yq)2=
(Ymk–Yq)2=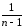 [
[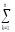 (Ymk)2
–
(Ymk)2
–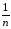 (
(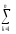 Yq)2],
которая является оценкой (s2нвыб≡
s2мг)межгрупповойдисперсииσмг2
= σА2+
σип2,
обусловленной и ожидаемым влиянием
фактораАи
неизбежным в ходе эксперимента влиянием
случайных факторов. В составе этой
дисперсии
составляющая от случайных ошибокσип
=
Yq)2],
которая является оценкой (s2нвыб≡
s2мг)межгрупповойдисперсииσмг2
= σА2+
σип2,
обусловленной и ожидаемым влиянием
фактораАи
неизбежным в ходе эксперимента влиянием
случайных факторов. В составе этой
дисперсии
составляющая от случайных ошибокσип
=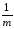 σέ2
– уменьшенная вm
раз дисперсияσип≡ σέ2
(σмг2=
σА2+
σέ2
– уменьшенная вm
раз дисперсияσип≡ σέ2
(σмг2=
σА2+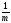 σέ2)
потому, что она входит в левую часть
этого соотношения через вычислениягруппового среднего, при которых
σέ2)
потому, что она входит в левую часть
этого соотношения через вычислениягруппового среднего, при которых
(при вычислениях
по формулеYmk
=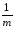
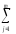 ykj)такие ошибки усредняются.
ykj)такие ошибки усредняются.
При справедливости соотношений:
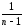 [
[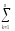 (Ymk)2
–
(Ymk)2
–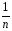 (
(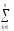 Yq)2]~ σмг
2 иσмг
2 =σА2
+
Yq)2]~ σмг
2 иσмг
2 =σА2
+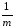 σέ2,
очевидно, что
σέ2,
очевидно, что
S
мг
~
σА2
+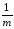 σέ
2 или
σέ
2 или
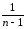 [
[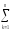 (Ymk)2
–
(Ymk)2
–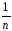 (
(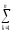 Yq)2]~
σА2
+
Yq)2]~
σА2
+ σέ
2
σέ
2
Переписав последнее соотношение в несколько ином виде, получаем:
s2
мг
=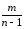 [
[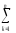 (Ymk)2
–
(Ymk)2
–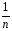 (
( Yq)2]~
mσА2
+ σέ2или s2мг
~
mσА2
+
σέ2,
Yq)2]~
mσА2
+ σέ2или s2мг
~
mσА2
+
σέ2,
откуда следует более точнаяпо сравнению с полученной на предыдущем листе выборочная оценкаs2А дисперсии σА2, обусловленной возможным влиянием исследуемого фактораА:
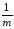 (sмг
2 –
sέ2)~ σА
2
(sмг
2 –
sέ2)~ σА
2
Приглядимся более внимательно к выборочной оценке s2мгдляσмг 2
s2мг
=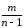 [
[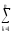 (Ymk)2 –
(Ymk)2 –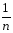 (
(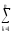 Yq)2]
Yq)2]
Во-первых, как обычно, s2 мг = (Σ мг) : f мг) Здесьf мг=n–1, следовательно,
(Σмг)=m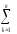 [(Ymk)2
–
[(Ymk)2
–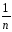 (
(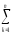 Yq)2].
Yq)2].
Во-вторых,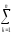 (Ymk)
2 =
(Ymk)
2 =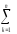 (
(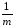
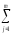 ykj)2
=
ykj)2
=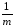 [
[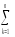
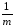 (
(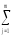 ykj)2]
=
ykj)2]
=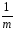 КЧА.
КЧА.
В-третьих,
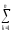 [(Yq)2
=
[(Yq)2
=
 (Yq)2(
(Yq)2(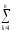 1)2
=
1)2
=
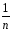 n
2(Yq)2
= n
(
n
2(Yq)2
= n
(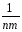

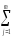 yij)2
=
yij)2
=
=
[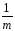
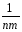 (
(
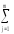 yij)2]
=
yij)2]
=
 КЧq
≡
КЧq
≡
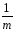 КЧq≡
КЧq≡
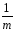 КЧ.
КЧ.
В итоге имеем:
(Σ
мг)
=m[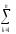 [(Ymk)2
–
[(Ymk)2
–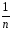 (
(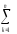 Yq)2]
=m{
Yq)2]
=m{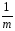 КЧА
–
КЧА
– КЧ}
= [КЧА
–КЧ]
КЧ}
= [КЧА
–КЧ]
Вспомним теперь ранее полученные соотношения:
(Σq)≡ (Σ)= [СК – КЧ] и(Σέ)= [СК – КЧА].
Сопоставив их с только что полученным (Σ мг)=[КЧА –КЧ], обнаруживаем:
(Σq)–(Σ έ)=[СК– КЧ –СК+ КЧА] = [КЧА –КЧ]= (Σмг).
Мы, следовательно, выяснили, что после вычисления выборочных оценок дисперсий mσА2 + σέ 2иσ2 можнонепосредственновычислить остаточную сумму(Σмг), которая потребуется для последующего нахождения выборочной оценкиs2вэдисперсии воспроизводимостиσвэ2 и уточнить оценку дляσА2.
Всё это означает, что представленный выше теоретически однофакторный эксперимент позволяет найти две (одна из которых уточняет другую) выборочные оценки для дисперсииσА2, обусловленной влиянием фактораА. Следовательно, такой эксперимент способен решить основную задачу дисперсионного анализа– задачуразделения составляющих общей дисперсии, а только что рассмотренные соотношения позволяют выполнить все необходимые вычисления, используя измеренные в ходе опытов значения{ylj} отклика.
Проблему решают три промежуточных интегральных параметра одной и той жевыборки СК, КЧ,КЧА.
