7.3 Двухфакторный дисперсионный анализ

7.3.1. Общие теоретические соображения

При проведении двухфакторного дисперсионного анализа опираются на более сложную модель «чёрного ящика», (см. рисунок) исследуемой системы.

Здравый смысл и очевидные соображения

ИССЛЕДУЕМАЯподсказывают, что для выявленияодновремен-

СИСТЕМА ного влияния факторов А и В на величину отк-

Фактор А Отклик У лика yследуетнесколько разизмерить этот

отклик при разныхуровнях фактора А (на при-

Фактор В мер: а₁,а₂,а₃, а₄,....а_n) приодном и том же

(например, при b_j) уровне фактора В, получив

Рис. 7.4при этомn штук (y_1j,y_2j, y_3j, y_4j, ..y_nj), по всей видимости, разных, значений отклика, а потомпроделать этоже ещёm – 1 раз, изменяя каждый раз уровень фактора В. Очевидно, что каждое конкретное значениеy_ijиз множества{y_ij}измеренных значений отклика будет складываться из реального среднего значенияY, прибавки к нему ± Δy_i, обусловленной влиянием (если такое влияние имеет мес- то) фактора Ана данномуровне, (уровне а_k) такой же прибавки ± Δy_u, обусловленной влиянием (если такое влияние имеет место) фактора В,на очередном(b_j) уровне и ошибки ±έ _ип измерительного прибора.

Фиксируем этот факт математически: y_ij =Y± Δy_i ± Δy_j±έ _ип. Это равносильно

(y_ij –Y)= (± Δy_i ± Δy_j±έ_ип) и говорит о том, что дисперсияσ² Генеральной совокупности{y}реальных значение отклика слагается из трёх составляющих:

- σ_έ² – дисперсии, обусловленной неточностью измерений(σ_έ²≡ σ_ип²);

- σ_А² – дисперсии, обусловленной ожидаемым влиянием фактора А;

- σ_В² – дисперсии, обусловленной ожидаемым влиянием фактора В.

Аддитивность дисперсии позволяет записать: σ² = σ_А² + σ_В² + σ_έ².

Таким образом, и здесь при обработке данных эксперимента, как и раньше, встаёт задача разделениясоставляющих общей дисперсии.

Рассмотрим способы такого разделения.

Прежде всего заметим, что для обозначения количества уровней второго фактора мы здесь используем символ m, которым в первом разделе было обозначено количество повторных измерения при одном и том же значении фактора А. Это «старое» значение символаmнаряду с «новым» сохраняется и здесь, что позволяет сохранить «старую» форму записи основных математических соотношений для случая двух факторов.

Теперь продолжим рассмотрение.

Предварительно следует найти выборочную оценку (s_έ²≡s²_ип) для дисперсия σ_έ², а потомs_В²иs_А²и отделить их друг от друга.

Начнём с вычисления общей выборочной дисперсииs_lj²≡s_q²≡s² на базе полученной в ходе представленного выше эксперимента выборки{y_ij}, объёмомq=nm.

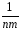
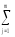
На базе множества разностей (y_ij –Y), гдеY=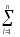(y_lj), i =1,2,3…k,, n, и j=1,2,3,.l ,,mможно сформировать исправленную выборочную дисперсию

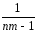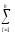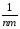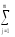
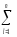s_ij² ≡ s²_mn≡ s²_q ≡ s² = [(y_ij)² –(y_ij)²] =

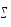= (_ij):f_ij = [СК_ij – КЧ_ij]:f_ij,, где:

- q = nm– объём выборки и потомуf_ij ≡f² = nm–1,

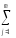
- СК_ij ≡СК =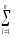(y_ij)² –сумма квадратов всех откликов, а

- КЧ_ij≡КЧ=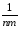(y_ij)² – усреднённый по всей выборке

квадрат суммы откликов.

Величина s² является выборочной оценкой (s² ~ σ²) дисперсииσ² Генеральной совокупности реальных значений отклика. Но и здесь (в случае двух факторов) это –

смешанная оценка (s² ~σ_А ²+σ _В ²+ σ_έ²).

Задача разделения дисперсий остаётся актуальной и усложняется. Решать её мы начнём, введя (как и раньше) в рассмотрение n малых выборок{y_kj}из общего массива измеренных значений отклика, которые получены принеизменных значениях фактора А. На базе каждой из таких малых выборок, кроме собственной групповой дисперсииs_k² можно вычислитьгрупповое среднеезначение отклика Y_k:=y_ij. Их (и групп, и средних) будет поn штук, все они будутразными, а средние– ещё и отличающимисяот всеобщего среднегоY =y_ij . Это означает, что будут существоватьnштук разностей типа (Y_k –Y), на базе которых длябольшойвыборки можно вычислить некую выборочную дисперсию(Y_k–Y)². А она является оценкой(s²(Y_k)≡ s²_k ≡s_Аε²)

межгрупповогоразброса– разброса значений групповых среднихY_k относительно всеобщего среднего Y. Очевидно, что этот разброс обусловлен как влияниемфактора А, так и влияниемслучайныхфакторов (потому и индекс «Аε»).

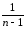
Математически это можно записать так: 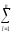(Y_k–Y)²~ σ_А ² + σ_Аип ² .

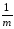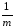
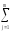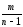
Влияние случайных ошибок σ²_Аип=σ_έ²здесь уменьшено вmраз потому, что они входят в левую часть этого соотношения через вычисления (по формуле Y_k =y_ij)группового среднего, при которых (при вычислениях) такие ошибки усредняются. Переписав обсуждаемое соотношение в целом в несколько ином виде (умножив обе его части наm), получаем: s²_k ≡s_Аε² =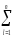(Y_k–Y)² ~ mσ _А ² + σ_έ².

Из этого следует, что роль итоговой суммы (∑_k) в выражении для выборочной дисперсииs²_Аε = (∑_Аε²):f_Аε, обусловленной ожидаемом в этом эксперименте фактора А, играет величинаm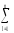(Y_k–Y)²,af_k≡f_Аε =n –1.

Это нам уже встречалось в параграфе 7.1, где мы получили:

(∑_k) =m[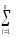(Y_i)² –(Y)²] =m{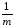КЧ_А –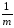КЧ_ij},

то есть (∑_k) ≡ (Σ_Аε)= КЧ_А –КЧ_ij= КЧ_А –КЧ.

Проведём точно такие жерассуждения относительно малых выборок{y_il} из общего массива{y_ij}, измеренных значений отклика, каждая из которых получена при неизменных значениях (например, приJ= l)фактораВ. Обнаруживаем, что таких выборок (строчных) будетm и что на их базе можно получитьещё однувыборочную оценку соответствующего межгруппового разброса групповых средних– разбросаY_l относительно всеобщего среднего Y, обусловленного ожидаемым влиянием фактора В.

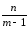
s²_Вε = 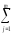(Y_l –Y) ² ~ nσ_В² + σ_έ².

Из этого следует, что роль итоговой суммы (∑_l)) ≡ (Σ _Вε)в выражении для выборочной дисперсииs²_l = (∑_Вε):f _Вε, обусловленной ожидаемом в этом эксперименте фактораB, играет величина

n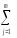(Y_l–Y)² af _Вε =m–1.

И здесь в итоге имеем:

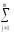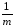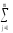(Σ _Вε)=n[(Y_l)² –(Y)²] =n{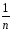КЧ_В –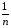КЧ_ij} = [КЧ_В –КЧ].

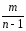
Обобщаем: s²_Аε =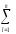(Y_k–Y)²=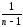[КЧ_А –КЧ] ~ mσ_А ² + σ_έ² и

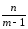
s²_Вε = 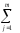(Y_l –Y)² =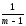[КЧ_B –КЧ] ~ nσ_В² + σ_έ².

С одой стороны, очевидно, что мы нашли раздельные выборочные оценки для дисперсий, обусловленных влияниями каждого фактора. С другой стороны, обе эти оценки –смешанные, в них присутствуют (замешаны) случайные ошибки. Всё это, казалось бы, заставляет нас продолжить поиск несмешанной выборочной оценки для дисперсии воспроизводимостиs_вэ² = (Σ_вэ):f_вэ.

Но, похоже, что делать дальше ничего не нужно. Ведь у нас есть (см. выше) опыт непосредственного нахождения остаточной суммы квадратовдисперсии воспроизводи-мостипутём вычитания (вспомните однофакторный эксперимент, для которого мы получили(Σ _вэ)= [СК – КЧ_А].

Конструируя аналогичным образом (Σ_вэ) для двухфакторного эксперимента, получаем: (Σ_вэ)= (Σ_ij)–(Σ _Вε)–(Σ_Аε), а при подробном развёртывании составляющих находим:(Σ_вэ)= [СК_ij– КЧ_ij–КЧ_А +КЧ_ij – КЧ_B +КЧ_ij], то есть

(Σ_вэ)= [СК_ij – КЧ_А – КЧ_B +КЧ_ij].

При таком подходе количество степеней свободы f_вэ для выборочной дисперсии воспроизводимости (s_вэ²) должно бытьf_вэ = f_lj– (f_А+ f_B)=

= nm-1- (n -1+ m-1) = nm-1- n +1- m+1=

= nm-1- n – m = n(m-1) - (m-1) = (m-1)(n -1).

Следовательно, несмещённой выборочной оценкой для дисперсии воспроизводимости двухфакторного эксперимента должна стать величина

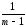
s_вэ² = (Σ_вэ):f_вэ= 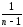[[СК_ij – КЧ_А – КЧ_B +КЧ_ij] =

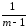
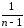= [[СК – КЧ_А – КЧ_B +КЧ].

.Всё это говорит о том, что и при планировании двухфакторного эксперимента можно воспользоваться точно такой жепрямоугольной план-матрицей, которая строилась при планировании однофакторного эксперимента, с тем, однако, отличием, что вместоm–кратного повторения опытов при каждом значении фактора А проводятся те жеmопытов приразных уровнях фактора В(см. макет план-матрицы на следующем листе). В связи с этим,немного изменятсяи алгоритмы обработки данных.

Наглядным образом-аналогом макета таблицы для данных двухфакторного эксперимента могла бы послужить m-этажная стеллаж-этажерка, на полках которой (друг под другом) размещены поn штук ячеек, по которым «разложены» результаты измерений отклика: весь массив{y_ij}, мощностьюnm.

Изменения алгоритмов обработки данных мы рассмотрим в следующем параграфе, а сейчас вспомним, что последнюю формулу мы «сконструировали по аналогии», опираясь на теоретический анализ однофакторного эксперимента. Убедительней было бы найти подтверждение правомерности такой аналогии путём анализа условий двухфакторного эксперимента, что явилось бы основанием для опоры на эту же аналогию и при трёх-, и при четырёх- (и т. д.) факторном эксперименте. При многофакторном эксперименте вообще. Ниже мы таким анализом и займёмся.

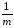
Обратимся ещё раз к малым выборкам. Ещё раз взглянем на одну из nуже рассмотрены выше малых выборок (вертикальный столбец) из общего массива{y_ij}измеренных значений отклика, которые получены при неизменных значенияхфактора А. Но теперь взглянем уже под другим углом зрения: рассмотрим разброс измеренных значенийy_ij относительно группового среднегоY_i(Y_i =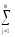y_ij) внутри каждой малой выборки.

При однофакторном анализе такой разброс был обусловлен толькослучайными ошибками, но здесь при смене номера опытаодновременноизменяется и уровень факто-ра В (этим и объясняется наличие индекс «_В»у выборочной дисперсииs²_Вl≡s²_Вε). Следовательно, только что представленная выборочная дисперсия являетсясмешаннойоценкой для суммы двух дисперсий такой малой выборки:

- дисперсии σ_В, обусловленных изменениями уровня фактора В, и

- дисперсии σ_έ, обусловленной случайными ошибками измерений.

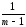
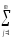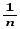В связи с этим можно записать: s²_Вэ =(y_ij–Y_i)² ~ σ_В ² +σ_έ².

Легко заметить, что это соотношение справедливо для любойи, следовательно, длякаждоймалой выборки (столбца) рассматриваемого здесь типа. Следовательно, усреднив это соотношение повсем таким выборкам, мы получимболее точнуювыборочную оценку, для которой уже не нужен исходный «столбиковый» индекс.

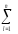
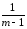
s²_Ввэ ≡ s²_вэ = s²_Вi = 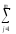(y_lj–Y_l)² ~ σ_В² + σ_έ².

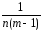
Или: s²_вэ ~ σ_В ² + σ_έ², то есть 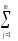(y_ij –Y_l)² ~ σ_В ² + σ_έ².

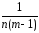
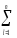
Это – хороший промежуточный результат в наших стараниях разделить дисперсии разного происхождения, потому, что он даёт возможность, рассмотрев два разныхсоотношения: 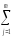(y_ij –Y_i)² ~σ_В ²+ σ_έ²и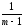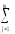(Y_j–Y)²~ σ_В 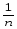² +σ_έ²,

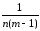
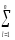
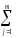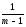
и разность левых ((y_lj–Y_l)² –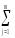(Y_j–Y)²) их частей. При этом, разностьлевыхчастей сравниваемых нами здесь оценочных соотношений:

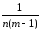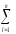
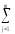[(y_ij –Y_l)²–n (Y_j–Y)²] остаётся выборочной оценкой разностиправыхих частей:

Σ _В ² + σ_έ²– σ_В² –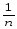σ_έ² =σ_έ²–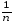σ_έ² =σ_έ² (1 –) =σ_έ²().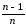

Это, в свою очередь, позволяет (не «конструировать», а математически точно выразить раздельную (несмешанную) оценку для дисперсииσ_έ², обусловленнойтолькослучайными ошибками.

Действительно, умножив обе только что представленные разности на ,

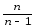получаем: 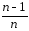(σ_έ²)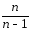=σ_έ² – с одной стороны, и

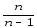
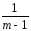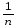
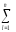
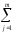[(y_ij –Y_l)²–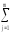(Y_j– Y)²]=

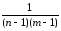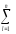
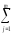= [(y_lj–Y_l)²–n (Y_j– Y)²] – с другой.

Всё это означает, что сконструированная здесь оценка

s²_вэ =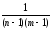 [(y_ij –Y_l)²–n(Y_j–Y)²], которая вычисляетсятолько по данным эксперимента, является несмешанной выборочной оценкой для дисперсии воспроизводимостиэксперимента(s²_вэ ~ σ²_вэ≡ σ_έ²).

По аналогии с предыдущим параграфом, этот же результат можно представить в несколько иной форме:

s²_вэ =(_вэ):f _Ввэ =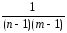 [СК _вэ– КЧ _вэ]_, где

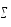( _вэ ) =[СК _вэ – КЧ _вэ ]–пока удобныеи чистоформальные обозначения,

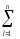
в которых: СК _вэ =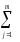(y_ij –Y_l)², а КЧ _вэ =n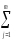(Y_j–Y)².

С каждым из этих соотношений будем разбираться отдельно.

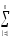
СК_вэ =(y_ij – Y_l) ² =[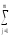(y_ij –Y_i) ²]=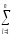[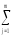(y_ij)²–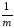(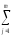y_ij)²]=

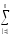
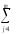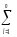
= (y_lj)² –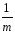(y_ij)² = СК_ij–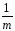(A_l)²= СК– КЧ_А.

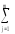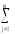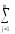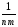
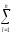
Второе:КЧ_вэ =n(Y_j–Y)²=n[(Y_j)²–2Y_jY + n (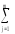y_ij)²] =

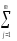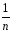
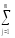
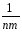
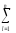
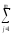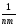
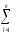
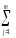= n(Y_j)² –2n (y_lj)(y_ij)+ n(y_ij)²1] =

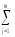
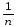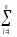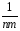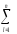
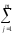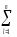
= (y_ij)² – 2(y_ij)² + nm(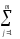y_ij)²]=

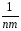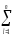
= КЧ_B – (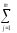y_ij)²] = КЧ_B – КЧ.

Таким образом, записанное вышеформально, соотношение:

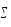(_вэ) = [СК _вэ – КЧ _вэ]=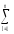(y_ij –Y_i)² – n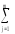(Y_j–Y)² уточняется:

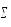(_вэ) = [СК _вэ – КЧ _вэ]=СК– КЧ_А – КЧ_B + КЧ.

Теперь вспомним, что при однофакторном эксперименте

(Σ_вэ)= [СК_ij– КЧ_А] =(Σ_lj)–(Σ_А) =[СК_ij– КЧ_ij–КЧ_А +КЧ_lj] и сопоставим с тем результатом, который получили только что.

С одной стороны, здесь (в двухфакторном эксперименте), действуя по аналогии, мы получили: (Σ_вэ)= [СК – КЧ_А– КЧ _B +КЧ].

С другой стороны, только что строго показали (Σ_выб)= (Σ_lj)–(Σ_А)–(Σ_B).

Но последнее можно переписать:

(Σ_вэ)= (Σ_lj)–(Σ_А)–(Σ_B) =[СК_ij – КЧ_ij]–[КЧ_А–КЧ_ij]–[КЧ_B –КЧ_ij] или

(Σ_вэ)= [СК – КЧ_А – КЧ_B +КЧ].

Оба результата совпадают. Следовательно, приведённые выше математические упражнения показали, что и при однофакторном, и при двухфакторном экспериментах остаточная сумма квадратов (Σ_вэ), необходимая для вычисления дисперсии воспроизводимости, может быть вычислена по данным экспериментанепосредственнопутём вычитания остаточных сумм факторных дисперсий из остаточной суммы общей дисперсии.

Мы убедились, что выделенные ранее промежуточные величины (СК иКЧ) оказались полезными и при рассмотрении двухфакторного эксперимента. Пригодятся они нам и далее.

При обобщении на случай многих (S) факторов полученный выше результат будет

выглядеть следующим образом: (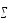_вэ) = [СК –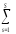КЧ_i +КЧ].

В этом выражении у величин: (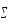_вэ), СК иКЧ не проставлены (из-за громоздкости) полагающиеся там поSштук индексов.

Вспомним теперь полученные ранее смешанные оценки:

s²_Аε~ mσ_А² + σ_έ² и s ² _В = ~ nσ_В² + σ_έ ²

Вычислив s²_вэ можно записать:

s²_Аε ~ mσ_А² + s²_вэ и s² _Вε ~ nσ_В² + s²_вэ или

{(s²_Аε – s²_вэ):m} ~ σ_A² и {(s²_Вε – s²_вэ):n} ~ σ_В ²

Таким образом, представленный в данном параграфе теоретически двухфакторный эксперимент способен представить достаточно данных для вычисления раздельных выборочных оценок длявсехслагаемых общей дисперсии (σ_ij² =σ_А ²+ σ_В² + σ_έ²) Генеральной совокупности возможных значений отклика исследуемой системы.