2.6. Нормальное распределение

Если случайная величина формируется под действием большого количества независимых факторов, вклад каждого из которых в значение случайной величины мал, то в силу центральной предель­ной теоремы эта случайная величина будет иметь нормальное распределение. В роли таких величин могут выступать: объем продаж в конкурентной отрасли или в промышленности в целом, суммарные инвестиции, суммарное потребление домашних хозяйств и тому подобные величины, имеющие аддитивную природу, то есть склады­вающиеся из многих малых взаимно независимых величин.

Основная особенность случайной величины состоит в том, что нельзя предвидеть, какое значение она примет в результате испытания. Однако при достаточно большом числе испытаний поведение суммы независимых случайных величин почти утрачивает случайный характер и становится почти закономерным. При увеличении числа слагаемых в сумме противоположные случайные колебания отдельных величин сглаживаются и распределение вероятностей суммы становится весьма простым, приближаясь при определенных условиях к нормальному распределению.

Нормальное распределение одной случайной величины Xоднозначно определяется лишь двумя параметрами: средним значением, обычно обозначаемым, и стандартным отклонением, обычно обозначае­мым. Это обычно обозначают так:Х=N(,)

2.6.1. Свойства нормального распределения

Рассмотрим основные свойства нормального распределения.

1⁰. Если ряд случайных величин(X₁,X₂, …X_n)имеет нормальное распределение, то их сумма(X₁+X₂+ …+X_n)или любая линейная комбинация (₁X₁+₂X₂+ …+_nX_n)также будет иметь нормальное распределение.

2⁰. Распределение величины , представляющей собой взвешенную суммупнезависимых нормально распределенных случайных величин Х_k=N(_k,_k) с параметрами_k и_k, также будет иметь нормальное распределение с параметрами и.

В частности, если все c_k=1/n, все_kи_k, одинаковы и равны_l,_l,соответственно, то=_l, а . Обозначая , имеем, таким образом,М[] = М[Х],[Х] =[Х]/. Отсюда видно, что разброс среднего арифметического независимых нормально распределенных случайных величин стремится к нулю при неограниченном увеличении числа этих величин. Если, например, взята достаточно большая репрезентативная выборка населения, то средний доход в выборке почти наверняка окажется близким к действительному среднему доходу населения.

2.6.2 Плотность вероятности и функция нормального распределения

График плотности вероятности нормального распределения имеет типичный колоколообразный вид и показан на рис. 2.5. Максимум этой функции находится в точке х=, а "растянутость" вдоль осиXопределяется параметром. Чем меньше значение этого параметра, тем более острый и высокий максимум имеет плотность нормального распределения. Аналитически плотность вероятности нор­мального распределения на интервале (-,+).

,

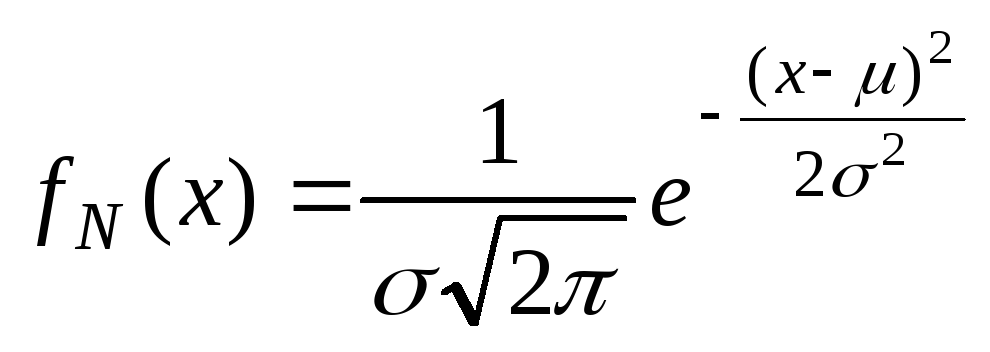а функция распределения

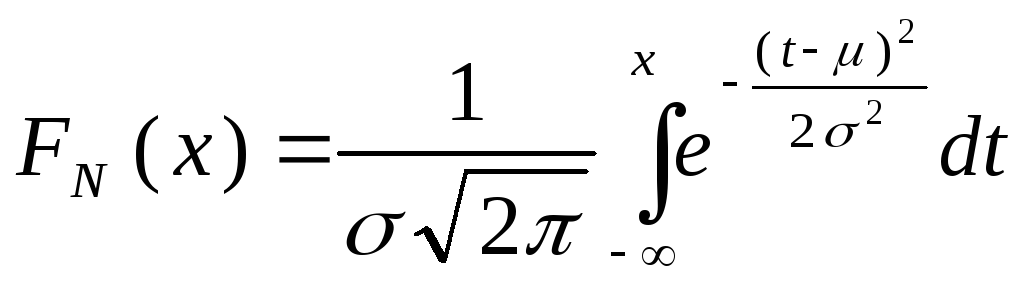
M[X]= , D[X]= ², V[X]=

Плотность вероятности нормального распределения пропорциональна величине ехр, гдеz- безразмерная величина, определяемая выражениемz=. Поэтому плотность нормального распределения достаточно быстро убывает при удалениихот среднего значения. Случайная величинаzимеет нулевое математическое ожидание и единичную дисперсию; это вытекает из их определений и свойств, учитывая, чтоz=.

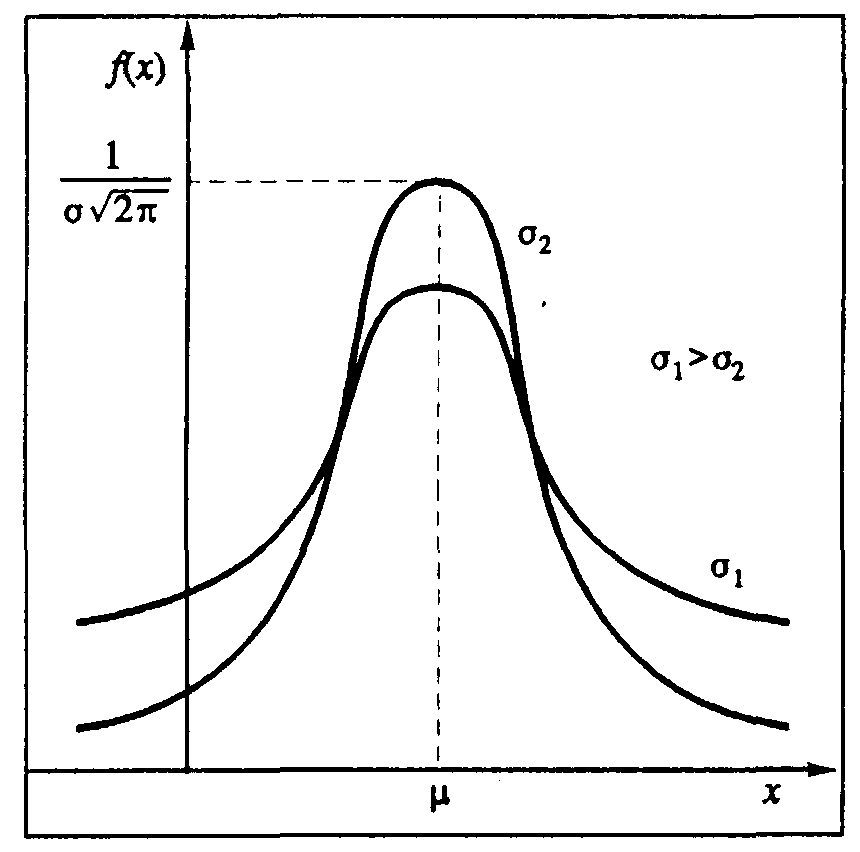
Рис. 2.5. Функция плотности вероятности нормального распре­деления

Она как и исходная случайная величинах,нормально распределена, но уже не зависит от каких-либо параметров. Поэтому достаточно протабулировать стандартное нормальное распределение (то есть представить в виде таблиц значения плотности вероятностиf_Z(z)), чтобы определить характеристики любой нормально распределенной величины. Эта функция называется плотностью стандартного нормального распределения. Стандартное нормальное распределение - это нормальное распреде­ление с параметрами = 0, =1 (ZN(0,1))

На практике чаще используют таблицы значений не плотности, а функции распределения стандартной нормальной величины F(x). Интересуясь, например, вероятностью того, что нормально распре­деленная случайная величинаXпопадает в интервалx₁X<x₂ мы вначале находим соответствующий интервал для нормально распределенной стандартной случайной величиныZ(z₁Z<z₂):z₁=иz₂=. Затем по таблице находим значения функции распределенияF{z₁)иF(z₂)и определяем вероятность попадания случайной величиныZв заданный интервал

Prob{z₁Z<z₂} =F{z₁) -F(z₂), совпадающую с искомой вероятностью попадания случайной вели­чиныXв заданный интервалProb{x₁X<x₂}. Геометрически эта вероятность изображается площадью под графиком функции плот­ности вероятности в интервале отx₁ доx₂.

Аналогично можно решать и обратную задачу - нахождения интервала, в который нормально распределенная случайная величина попадает с заданной вероятностью. Эта процедура часто используется в задачах теории оценивания и проверкигипотез. Так, например, пусть мы хотим проверить гипотезу о равенстве среднего значения нормально распределенной случайной величиныX(для генеральной совокупности) нулю, допуская вероятность ошибки 0,05 в случае, если эта гипотеза верна. В этом случае выборочное значение стандартной нормально распределенной случайной величиныZдолжно попадать в такой интервал, что вероятностьProb{z₁Z<z₂}= 0,95. Из этого условия и соображений симметрии можно найти границы интервала - критические значенияz_кр=z₂=-z₁, такие, чтоProb{Z z₁} =Prob{Z z₂}= 0,05/2 = 0,025.

Сравнивая выборочное значение величины называемое z-статистикой с критическим значениемz_кр, мы принимаем (если z₁z<z₂) или отвергаем (еслиz<z₁ или z₂<z) проверяемую гипотезу с точ­ностью (уровнем значимости)ε=0,05 (5%).