3.3.2 Свойства оценок мнк

Для того, чтобы полученные МНК оценки a и b обладали желательными свойствами, сделаем следующие предпосылки об отклонениях _i:

1) величина _iявляется случайной переменной;

2) математическое ожидание _i, равно нулю: М[_i] =0;

3) дисперсия _iпостоянна:D[_i] =D[_i] =²для всехi,j;

4) значения _iнезависимы между собой. Откуда вытекает, в частности, что

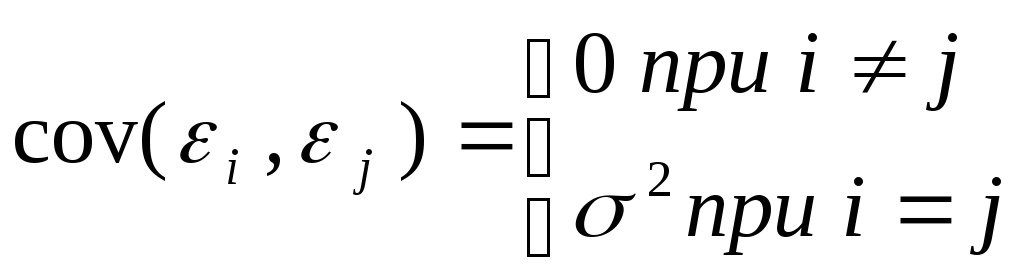
Известно, что, если условия 1)-4) выполняются, то оценки, сде­ланные с помощью МНК, обладают следующими свойствами:

1) Оценки являются несмещенными, т.е. математическое ожида­ние оценки каждого параметра равно его истинному значению:М[а] =,М[b]=. Это вытекает из того, чтоМ[_i] =0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2) Оценки состоятельны, то есть дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю:;

Иначе говоря, если nдостаточно велико, то практически навернякаaблизко к, аbблизко к: надежность оценки при увеличении выборки растет.

3) Оценки эффективны, они имеют наименьшую дисперсию относительно истинного значения оцениваемых параметровипо сравнению с любыми другими оценками, линейными относительно величину_i.В англоязычной литературе такие оценки называютсяBLUE(Best Linear Unbiased Estimators -наилучшие линейные несмещенные оценки).

Перечисленные свойства не зависят от конкретного вида распределения величин _i, тем не менее, обычно предполагается, что они распределены нормальноN(0,²).Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но среди всех несмещенных оценок.

Если предположения 3) и 4) нарушены, то есть дисперсия возмущений непостоянна и/или значения _iсвязаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности - нет.

Рассмотрим теперь процедуру оценивания параметров парной линейной регрессии аиb.Для того, чтобы функция

Q=

достигала минимума, необходимо равенство нулю ее частных производных:



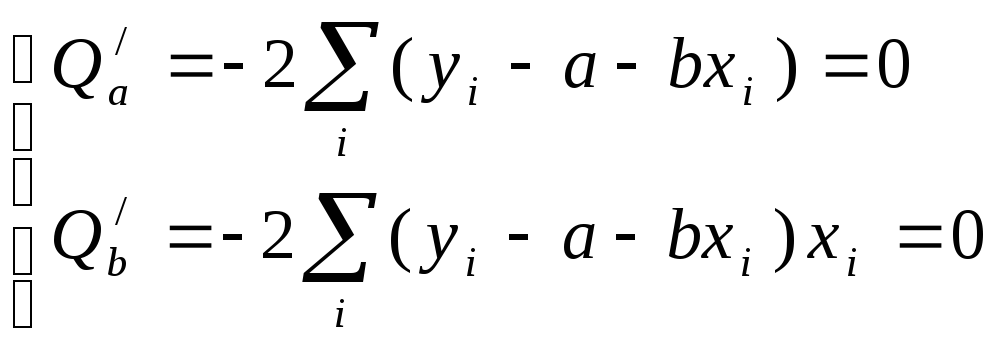
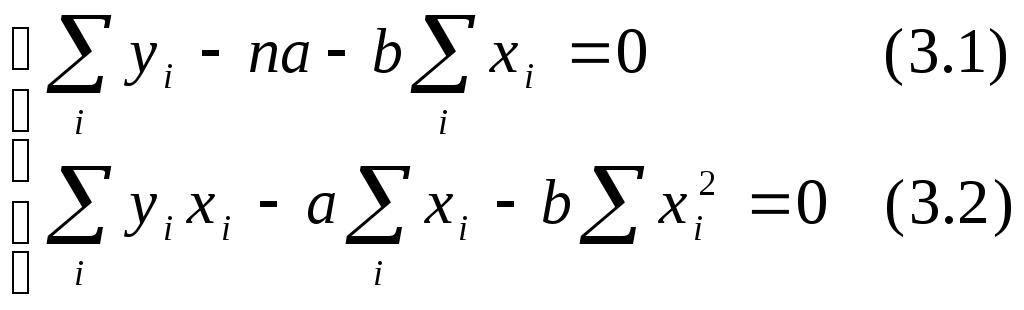
Если уравнение (3.1) разделить на п,то получим(здесьсредние значенияхиу).Таким образом, линия регрессии проходит через точку со средними значениями. Подставив величинуаиз (3.1) в (3.2), получаем

Откуда

;

Иначе можно записать, что

(где r -коэффициент корреляциихи у). Таким образом, коэффициент регрессии пропорционален показателю ковариации и коэффициенту корреляциихиу,а коэффициенты этой пропорциональности служат для соизмерения перечисленных разноразмерных величин. Оценкиaиb,очевидно, являются линейными относительноу_i(еслих _iсчитать коэффициентами) - выше об этом упоминалось.

Итак, если коэффициент rуже рассчитан, то легко рассчитать коэффициент парной регрессии, не решая системы уравнений. Ясно также, что если рассчитаны линейные регрессиих(у)иу(х),то произведение коэффициентовb_xиb_yи, равноr²:

3.4. Анализ статистической значимости коэффициентов линейной регрессии

Величины y_i, соответствующие даннымx_iпри некоторых теоретических значенияхи, являются случайными. Следовательно, случайными являются и рассчитанные по ним значения коэффициентоваиb.Их математические ожидания при выполнении предпосылок об отклонениях_iравны, соответственно,и. При этом оценки тем надежнее, чем меньше их разброс вокругаиb, то есть дисперсия. По определению дисперсииD[b] =М[b-]²,D[a] =М[a-]². Надежность получаемых оценокаиbзависит, очевидно, от дисперсии случайных отклонений_i, но поскольку поданным выборки эти отклонения (и, соответственно, их дисперсия) оценены быть не могут, они заменяются при анализе надежности оценок коэффициентов регрессии на отклонения переменнойуот оцененной линии регрессииe_i =y_i-a-bx_i.

Можно доказать (доказательство опускаем), что

D[b]=S_b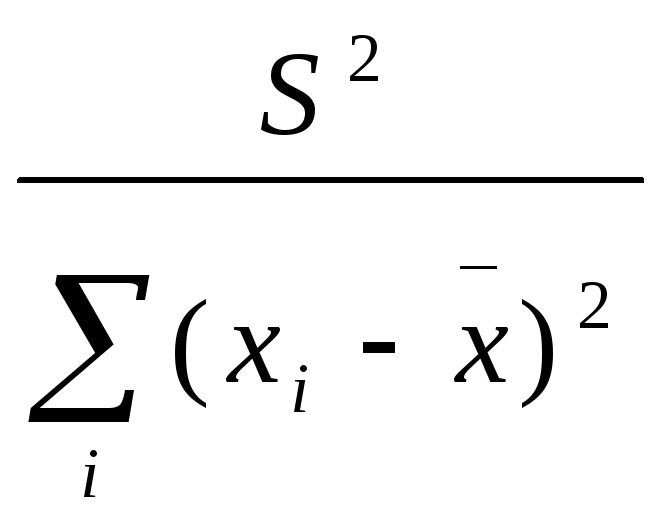²=; D[a]=S_a²=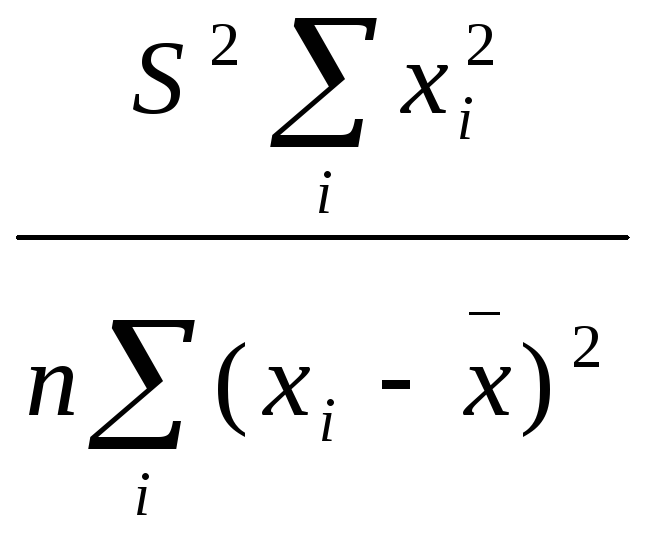;где

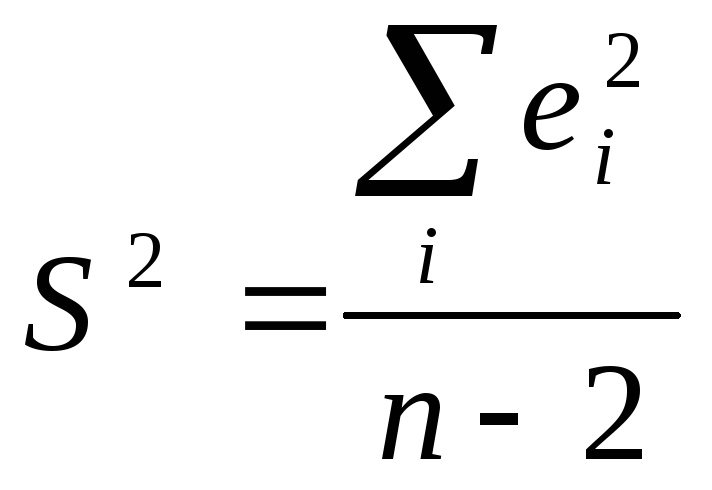
- мера разброса зависимой переменной вокруг линии регрессии (необъясненная дисперсия). S_aиS_b- стандартные отклонения случайных величинаиb. Полученный результат можно проинтерпретировать следующим об­разом.

Коэффициент bесть мера наклона линии регрессии. Очевидно, чем больше разброс значенийувокруг линии регрессии, тем больше (в среднем) ошибка в определении наклона линии регрессии. Если такого разброса нет совсем (_i= 0 и, следовательно,²=0), то прямая определяется однозначно и ошибки в расчете коэффициентоваиbотсутствуют (а отсюда и значениеS²,"замещающее"²,равно нулю).

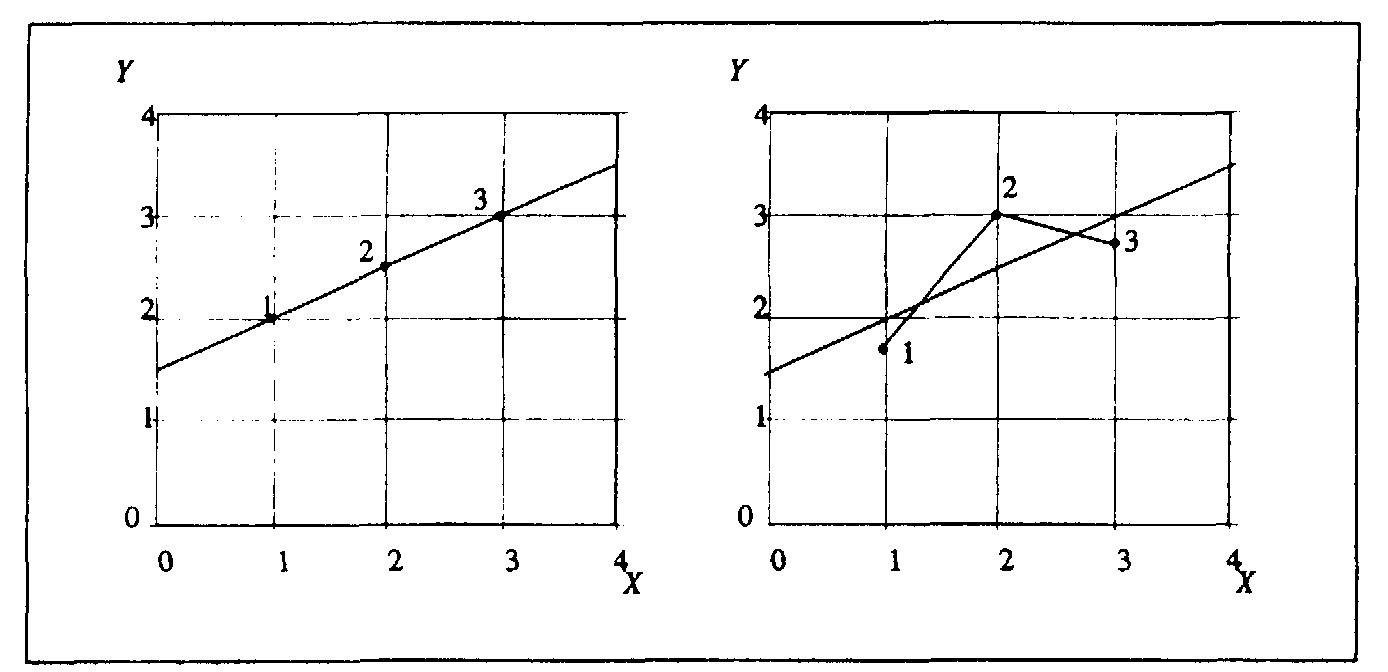
a b

Рис. 3.5

На рис. 3.5а отклонения в значениях переменной уот линии регрессии отсутствуют, и через три точки проводится та же прямая, что и через любые две из них. На рис. 3.5bчерез три точки проводится такая же линия регрессии, но колебания значений переменной у вокруг этой линии значительны. Поэтому через пары точек (1,2) и (1,3) проходят совершенно разные прямые, отличные от общей прямой. Следовательно, стандартные ошибки коэффициентов регрессии в этом случае будут значительными.

В знаменателе величины D[b] стоит сумма квадратов отклоненийхот среднего значения.Эта сумма велика в том случае, если регрессия оценена на достаточно широком диапазоне значений переменнойх,и в этом случае, при данном уровне разбросаy_i, очевидно, ошибка в оценке величины наклона прямой будет меньше, чем при малом диапазоне изменения переменнойх.Попробуйте провести прямую по двум точкам: если х₁и х₂, лежат рядом, то даже небольшое изменение одного изу_iсущественно меняет наклон прямой (если х₁и х₂, далеки друг от друга - ситуация обратная).

Так, на рисунке 3.5 через пары точек (1,2) и (1а,2) проходят одни и те же прямые, в то же время разброс переменной хдля первой из пар больше. Если у второй точки из каждой пары изме­нить значение переменнойу(перевести ее в точку 2а или 2b), то наклон прямой для пары (1,2) изменится значительно меньше, чем для пары (1а,2).

Кроме того, чем больше (при прочих равных) число наблюдений п,тем больше и, тем самым, меньше стандартная ошибка оценки. Дисперсия свободного члена уравнения регрессии равнаD[a]=D[b]

-она пропорциональнаD[b]и, тем самым, также соответствует уже сделанным пояснениям о влиянии разбросаy_iвокруг регрессионной прямой и разбросаx_iна стандартную ошибку. Чем сильнее меняется наклон прямой, проведенной через данную точку(),тем больше разброс значений свободного члена, характеризующего точку пересечения этой прямой с осьюу.Кроме того, дисперсия и стандартная ошибка свободного члена тем больше, чем больше средняя величинах_i².При больших по модулю значенияхх даже небольшое изменение наклона регрессионной прямой может вызвать большое изменение оценки свободного члена, поскольку в этом случае в среднем велико расстояние от точек наблюдений до осиу.

Рис. 3.6

На рис. 3.6 через пары точек (1,2) и (3,4) проходит одна и та же прямая линия. Ее свободный член равен а.Для второй из этих пар значения переменнойхбольше по абсолютной величине (при одинаковом разбросе значенийхиу).Если в первой из этих пар от точки 1 перейти к точке 1а, а во второй - от точки 3 к 3а, что вызвано одинаковыми изменениями одного из значений переменнойу,то обе линии становятся горизонтальными. Изменения коэффициента наклона прямой одинаковы, но свободный член в первом случае становится равнымa₁, а во втором –a₂,-таким образом, он меняется значительно больше там, где больше абсолютные значения переменнойх.

Формально значимость оцененного коэффициента регрессии b может быть проверена с помощью анализа его отношения к своему стандартному отклонению . Эта величина в случае выполнения исходных предпосылок модели имеетt-распределение Стьюдента с (n-2) степенями свободы(п -число наблюдений). Она называетсяt-статистикой:

.

Дляt-статистики проверяется нулевая гипотеза, то есть гипотеза о равенстве ее нулю. Очевидно,t= 0 равнозначноb= 0, посколькуt пропорциональнаb.

Рис. 3.7