kurs_lekcii_mo_matematicheskomu_analizu / Понятие непрерываности функций

f2(x)

f1(x)

ЛЕКЦИЯ 5. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ.

Графиками числовых последовательностей являются множества точек, которые находятся на некотором расстоянии друг от друга (дискретное множество точек). Графиком же, например, степенной функции является кривая, которая похожа на ”сплошную”, ”непрерывную” линию. Оказывается, это явление характеризует точное математическое понятие непрерывности функции, которое будет введено в данном параграфе.

1.Непрерывные функции

Пусть функция f (x)	определена в точке x0 и в некоторой ее окрестности.
Обозначим x − x0 =	x , откуда x = x0 + x, x – приращение аргумента в точке

x0.

Говорят, что для перехода от значения аргумента x0 к значению x первоначальному значению аргумента придано приращение x .

Приращением y функции y = f (x) , соответствующим приращению аргумента x в точке x0 , называется разность

y = f (x0 + x) − f (x0).

Например, приращением функции y = x3 , которое соответствует приращению x аргумента x в точке x0 , будет величина

y = (x0 + x)3 − x30 = 3x20 x + 3x0(Δx)2 + (Δx)3.

Определение 1. Функция называется непрерывной в точке x0 , если бесконечно

малому приращению	x аргумента x в точке x 0 соответствует бесконечно малое
приращение функции	y , т. е.
	lim y =	lim [f (x0 + x) − f (x0)] = 0.
	x→0	x→0

Отсюда функция y = f (x) непрерывна в точке x0 , если

lim f (x) = f (x0),

x→x0

т. е. предел функции в точке x0 равен значению функции в этой точке.

Утверждение 1. Если функции f1(x) и f2(x) непрерывны в точке x 0 , то непрерывны в этой точке также их алгебраическая сумма f1(x)± ±f2(x) , произведение f1(x)f2(x) и при условии f2(x) =6 0 частное .

Эта теорема вытекает из свойств пределов.

Утверждение 2. Если функция u = ϕ(x) непрерывна в точке x 0 , а функция y = f (u) непрерывна в точке u0 = ϕ(x0) , то сложная функция y = f (ϕ(x)) непрерывна в точке x 0 .

1

Доказательство. Ввиду непрерывности u = ϕ(x) имеем

lim ϕ(x) = ϕ(x0) = u0.

x→x0

Поэтому в силу непрерывности f (u)

lim f (ϕ(x)) = f ( lim ϕ(x)) = f ( lim u) = f (u0) = f (ϕ(x0)).
x→x0	x→x0	u→u0

Теорема доказана.

Утверждение 3. Все основные элементарные функции непрерывны там, где они определены.

y = C (постоянная) непрерывна (Δy = 0) ;

y = x непрерывна ( lim	y = lim x = 0 ); y = xn , n натуральное число, также
x→0	x→0

непрерывна. Непрерывность тригонометрических функций sin x, cos x имеет место всюду; функции tg x, ctg x непрерывны там, где они определены.

Определение 2. Функция f (x) непрерывна в точке a справа (слева), если

lim f (x) = f (a)	( lim f (x) = f (a)).
x→a+0	x→a−0

Замечание 1. Если f (x) непрерывна в точке a и слева, и справа, то она непрерывна в этой точке. Действительно, в этом случае существует предел функции в точке a , равный f (a) .

2.Точки разрыва

Точки, в которых функция не обладает свойством непрерывности, называются

точками разрыва этой функции.

Выясним возможные типы точек разрыва.

1. Устранимый разрыв

Точка a называется точкой устранимого разрыва функции y = f (x) , если предел функции f (x) в точке a существует, но в самой точке a значение f (x) либо не существует, либо не равно пределу f (x) в этой точке.

Таким образом, изменив значение функции всего в одной точке a, можно устранить разрыв.

2. Разрыв первого рода

Точка a называется точкой разрыва первого рода, если в этой точке f (x) имеет конечные, но не равные друг другу правый и левый пределы

lim f (x) 6= lim f (x).

x→a+0

x→a−0

Такой разрыв можно назвать скачком.

3. Разрыв второго рода

Точка a называется точкой разрыва второго рода, если в этой точке f (x) не имеет, по крайней мере, одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.

2

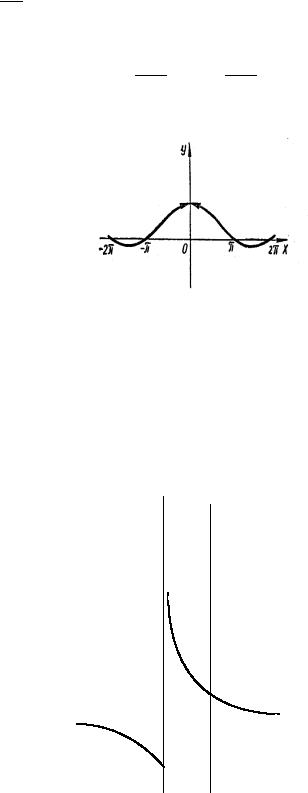
Пример 1. Показать, что точка x = 0 является точкой устранимого разрыва для

функции f (x) = sin x .
x
Решение. Функция f (x) = sin x не определена при x = 0, но определена при всех
x
x =6 0. Односторонние пределы функции в точке x = 0 равны между собой:
lim	sin x =	lim	sin x = 1.
x→−0	x	x→+0	x

Тогда по определению заключаем, что точка x = 0 является точкой устранимого разрыва.

1

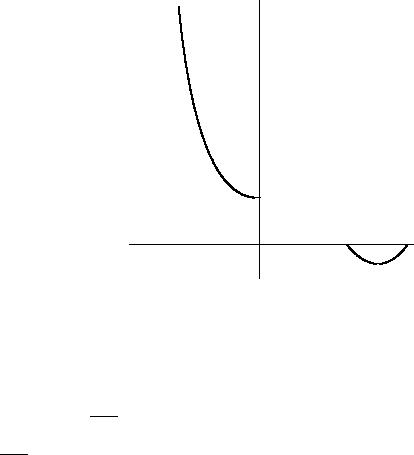
Пример 2. Исследовать на непрерывность функцию y = 3

x+1

при x1 = 2 и x2 =

−1 . Определить тип разрыва. Сделать схематический чертеж.

Решение. Элементарные

функции

в

точках

определения непрерывны. Значит,

1

1

функция y = 3

x+1

(элементарная, y(2) = 3 3 ) непрерывна в точке x1 = 2 . В точке

x2 = −1 она не определена. Найдем

1

1

lim

3

x+1

= ∞;

lim

3

x+1

= 0.

x→−1+0

x→−1−0

Имеем разрыв второго рода. Найдем еще

1

lim 3

x+1

= 1.

x→∞

y

6

			1
		-1	0	-
				x
Пример 3. Исследовать на непрерывность функцию
f (x) =		x2 + 1	при	−∞ < x ≤ 0,
		x + 1	при	0 < x < π,
			при
		sin x		π ≤ x < ∞.

3

Найти точки разрыва функций. Сделать чертеж.

Решение. Область определения функции (−∞, ∞) . В интервалах (−∞, 0), (0, π), (π, ∞) функция непрерывна, так как в этих интервалах она задана элементарными функциями. Поэтому разрывы возможны в точках x = 0, x = π , в которых изменяется аналитическое задание функции

f (0) = (x2 + 1)|x=0 = 1,	lim f (x) =	lim (x2 + 1) = 1,
x→0−0		x→0−0
lim f (x) =	lim (x + 1) = 1.
x→0+0	x→0+0
В точке x = 0 функция непрерывна, так как

lim f (x) =	lim f (x) = f (0) = 1.
x→0−0	x→0+0

Далее,

f (π) = sin π = 0, lim f (x) = lim (x + 1) = π + 1,

	x→π−0	x→π−0
lim	f (x) = lim	sin x = sin π = 0.
x→π+0	x→π+0
В точке x = π функция терпит разрыв 1-го рода, так как
	lim f (x) =6	lim f (x).
	x→π−0	x→π+0
		6y

x

-

0 π

Пример 4. Исследовать на непрерывность и найти точки разрыва функции

	f (x) =	|x+1|	· x −	1	,	при	x =6 −1,
		x+1
			1,			при	x = −1.

Решение. Данная функция определена для всех значений x . Если x > −1 , то x+1 >

0 , |x + 1| = x + 1 и |xx+1+1| = 1 . В этом случае f (x) = 1x − 1 = x − 1 , поэтому для всех значений x > −1 функция непрерывна как многочлен первой степени. Аналогично, при

x < −1 , |x+1| = −1 и f (x) = −x − 1 непрерывна как многочлен первой степени.

x+1

4

Исследуем точку x0 = −1 . Выясним, существует ли предел функции в этой точке. Вычислим односторонний предел при x → −1 слева и справа. При x < −1 , f (x) = −x − 1 ; а при x > −1 , f (x) = x − 1 , поэтому

lim	f (x) = lim		(−x − 1) = 1 − 1 = 0,
x→−1−0		x→−1−0
lim	f (x) =	lim	(x − 1) = −1 − 1 = −2.
x→−1+0		x→−1+0

Следовательно, односторонние пределы функции f (x) в точке x0 = −1 существуют, но не равны между собой; в этой точке данная функция имеет разрыв первого рода. Ее график состоит из двух полупрямых и точки.

f (x) =		1, 1	,	при	x = −1,
		x −		при	x > −1,
				при
	−x − 1,				x < −1.

Пример 5. Исследовать на непрерывность и найти точки разрыва функции

6

f (x) = (x − 3)2 .

Решение. Функция определена во всех токах, кроме точки x = 3. Найдем односторонние пределы. Имеем

6

lim = +∞,

x→3−0 (x − 3)2

6

lim = +∞.

x→3+0 (x − 3)2

Точка x = 3 является точкой разрыва второго рода.

5

Пример 6. Исследовать на непрерывность и найти точки разрыва функции

	y =			1	.
		1 + 21/(x−1)
Эту функцию можно представить как сложную:
1				1
y =			,	где u =			.
	1 + 2u					x − 1
Знаменатель первой дроби нигде в нуль не обращается ( y =								1	непрерывная функция
								1+2u
при любом значении u ). Функция u =				1/(x − 1 ) непрерывна для всех значений x ,

кроме x = 1 . Данная сложная функция непрерывна для всех x 6= 1 . При x → 1 слева x − 1 < 0 и, следовательно, 1/(x − 1) → −∞ , a 21/(x−1) → 0 , поэтому

lim	1	=	1	= 1.
	1 + 21/(x−1)
x→1−0			1 + 0

При x → 1 справа x − 1 > 0 и, следовательно, 1/(x − 1) → ∞ и 21/(x−1) → ∞ , поэтому

1

lim = 0.

x→1+0 1 + 21/(x−1)

Таким образом, пределы справа и слева существуют, но не равны, то точка x0 = 1 является точкой разрыва первого рода.

6

3.Свойства функции, непрерывной на отрезке

Функция y = f (x) называется непрерывной на [a, b], если она непрерывна в каждой точке (a, b), непрерывна в точке a справа и непрерывна в точке b слева.

Утверждение 4. Пусть f (x) непрерывна на [a, b]. Тогда имеем:

1. Функция f (x) ограничена на [a, b], т. е. существуют такие числа m , M , что

x [a, b] : m ≤ f (x) ≤ M. y

M 6

m						-
		a		b			x

2. Функция f (x) достигает на [a, b] своих наименьшего и наибольшего значений,

т. е. α, β [a, b] :
f (α) = min f (x),	f (β) = max f (x).
x [a,b]	x [a,b]
y
6

								-
a β			α			b x

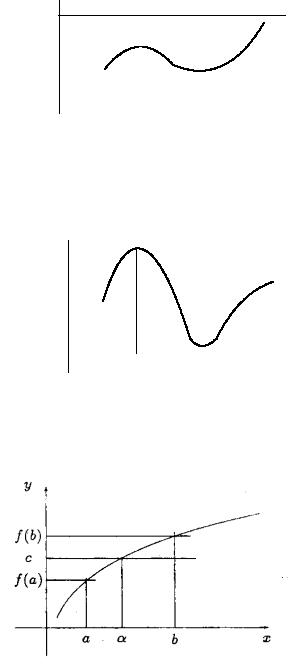
3. Если c лежит между f (a) и f (b), то α [a, b] : f (α) = c.

Теорема приводится без доказательства.

Замечание 2. Если f (x) непрерывна на [a, b], f (a)·f (b) < 0, то уравнение f (x) = 0 имеет на [a, b] хотя бы один корень.

7