kurs_lekcii_mo_matematicheskomu_analizu / Определение предела

ЛЕКЦИЯ 2. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ, ФУНКЦИИ. ЧИСЛО e.

1.Определение предела функции

Введем важнейшее в математике понятие предела функции, играющее фундаментальную роль в математическом анализе.

Пусть функция y = f (x) определена в некоторой окрестности точки x0, т. е. в некотором интервале с центром в точке x0, кроме, быть может, самой точки x0. Пусть независимая переменная неограниченно приближается к числу x0, т. е. мы придаем x значения, сколь угодно мало отличающееся от x0. Запишем это так: x → x0 (читается ¾ x стремится к x0 ¿).

Может оказаться при этом, что соответствующие значения f (x) неограниченно приближаются к некоторому числу A, тогда говорят, что число A есть предел функции f (x) при x, стремящемся к x0.

Определение 1. Число A называется пределом функции y=f(x) при x → x0, если для всех x , достаточно мало отличающихся от числа x0, соответствующие значения функции f (x) сколь угодно мало отличаются от числа A.

Это записывается так:
lim f (x) = A			или f	x	A, при x	→	x0.
x	→	x0		( ) →
Точка x0 называется предельной точкой.
Заметим, что выражение ¾ f (x)			сколь угодно мало отличается от A ¿ означает, что

для любого (сколь угодно малого числа) ε выполняется неравенство

|f (x) − A| < ε.

Выражение ¾ x достаточно мало отличается от x0 ¿ означает, что существует такое малое число δ, что неравенство |x − x0| < δ достаточно для выполнения некоторого неравенства с f (x).

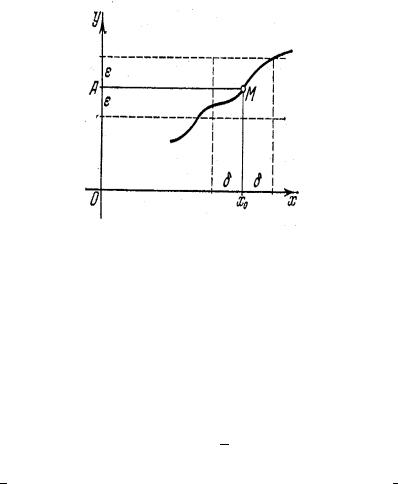
Определение 2. Число A называется пределом функции y=f(x) при x → x0, если для любого числа ε > 0 существует такое число δ(ε) > 0 , что для всех x =6 x0, удовлетворяющих условию |x − x0| < δ, имеет место неравенство

|f (x) − A| < ε.

Наличие у функции y = f (x) при x → x0 предела, равного A, графически иллюстрируется следующим образом.

1

Пример 1. Показать, исходя из определения предела функции, что lim(3x−1) = 2.

x→1

Решение. Зададим число ε > 0. Для того чтобы имело место неравенство

|(3x − 1) − 2| < ε

или

3|x − 1| < ε,

достаточно, чтобы было выполнено неравенство

|x − 1| < 3ε .

Возьмем δ = 3ε , тогда оказывается, что для любого ε нашлось δ = 3ε > 0, такое, что при всех x 6= 1, для которых |x − 1| < δ , следует неравенство |(3x − 1) − 2| < ε. Здесь оговорка x 6= 1 не существенна, т. к. неравенство выполняется и при x = 1.

Пример 2. Показать, исходя из определения предела функции, что

lim x2 = 4.

x→2

Решение. Пусть ε любое положительное число. Требуется доказать, что можно

подобрать такое δ > 0 , что для

всех x , удовлетворяющих неравенству

|

x

− 2|

< δ, будет

2

выполняться неравенство 0 < |x − 4| < ε .

2

Если |x −2| < δ , то |x + 2| = |x −2 + 4| ≤ |x −2|+ 4 < δ + 4 и |x −4| = |x −2||x + 2| <

δ(δ + 4) . Здесь мы воспользовались неравенствами

|a + b| ≤ |a| + |b|, |ab| = |a||b|.

Теперь

для выполнения неравенства

|

x2

− 4|

< ε достаточно потребовать δ

δ

ε .

δ

2

(

+ 4) =

То есть

+ 4δ − ε = 0 . Решая данное квадратное уравнение относительно δ,

получаем

√

√

два корня δ1 = −2 + 4 + ε и δ2 = −2 −

4 + ε . Второй корень отбрасываем, так как δ

должно быть положительным.

√

Таким образом, для любого ε

найдется δ

= −2 +

+ ε такое, что из неравенства

x

< δ следует неравенство

x

2

4

2

= 4 .

|

− 2|

|

− 4|

< ε . То есть lim x

x

→

2

2

В дальнейшем для нахождения пределов подобную проверку (существования δ по любому ε ), часто очень громоздкую и затруднительную можно будет проводить, используя свойства пределов.

Рассмотрим ситуацию, когда независимая переменная x функции y = f (x) неограниченно возрастает, т. е. становится больше любого заданного положительного числа. При этом говорят, что x стремится к плюс бесконечности, и записывают x → +∞. Если x неограниченно убывает, т. е. становится меньше всякого заданного отрицательного числа, то говорят, что x стремится к минус бесконечности, и записывают x → −∞.

Если оказывается, что при x → +∞ (x → −∞) соответствующее значение f (x) сколь угодно приближается к некоторому числу A, то говорят, что A есть предел f (x)

при x → +∞ (x → −∞).

Рассмотрим случай, когда x → +∞.

Определение 3. Число A называется пределом функции y = f (x) при x → +∞, если для любого ε > 0 существует такое число N (ε) > 0, что для всех значений x, удовлетворяющих неравенству x > N выполняется неравенство |f (x) − A| < ε.

Аналогично дается определение при x → −∞.

Если при x → +∞ и при x → −∞ функция стремится к одному и тому же пределу

A. Тогда пишут
lim f (x) = A или		f (x)	→	A при x	→ ∞	.
x	→∞
Определение 4. Число A называется пределом функции						y = f (x) при x → ∞,
если для любого ε > 0 существует такое число				N (ε) > 0, что для всех значений x,

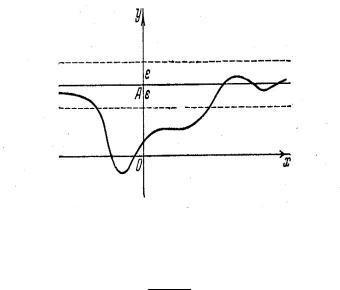
удовлетворяющих неравенству |x| > N выполняется неравенство |f (x) − A| < ε.

Геометрическая иллюстрация этого дается рисунком:

Пример 3. Доказать, исходя из определения предела функции, что

x2

lim = 1.

x→∞ x2 + 1

3

Решение. Пусть ε любое положительное число. Требуется доказать, что можно подобрать такое N > 0 , что для всех x, удовлетворяющих неравенству |x| > N, будет выполняться неравенство

x2 + 1 − 1

< ε.

x2

Если

2

2

.

x > N , то x > N

| |

x2

+ 1 <

N 2 .

+ 1 − 1

= x2 + 1 < N 2

x2

1

1

1

Следовательно, для

выполнения неравенства

x2 + 1 − 1

< ε

x2

1

достаточно найти N из условия

/N

2

есть N

1

= ε , то

= √

ε

. Итак, для любого ε найдено

N , что из неравенства

|

x > N

следует неравенство

x2

− 1

< ε. Доказано, что

2

+1

такое x2

|

x

xlim

= 1 .

x2+1

→∞

2.Предел последовательности. Число e

Рассмотрим теперь функцию натурального аргумента:

y = f (n), n = 1, 2, 3, ... .

Значения y1 = f (1), y2 = f (2), ..., yn = f (n), ..., принимаемые функцией целочисленного аргумента, образуют последовательность.

Определение 5. Последовательностью {yn} называется бесконечное перенумерованное множество чисел, расположенных в порядке возрастания номеров.

Например, члены геометрической прогрессии 12 , 14 , 18 , . . . образуют последовательность

1 .

2n

Определение 6. Число A называется пределом последовательности {yn}, если при всех достаточно больших значениях номеров n соответствующие значения yn сколь угодно мало отличаются от A.

Отсюда видно, что понятие предела последовательности является частным случаем предела функции, когда аргумент стремится к бесконечности.

Предел последовательности обозначается так:

A = lim yn.

n→∞

Определение 7. Последовательность {yn} называется ограниченной сверху, если существует такое число M, что для всех n

yn < M.

4

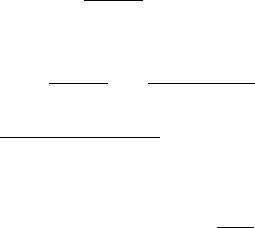
Определение 8. Последовательность {yn} называется монотонно возрастающей, если при всех n

yn < yn+1.

Укажем, в виде теоремы, признак существования предела.

Теорема 1. Если последовательность

{yn}

возрастает и ограничена сверху, то она

имеет предел.

Существование предела такой последовательности очевидно из рисунка.

yn

6

r

r

r

r

r

r

r

r

-

n

1

2

3

4

5

6

Рассмотрим один важный предел последовательности, называемый вторым замечательным пределом.

Теорема 2. Последовательность

yn =

n

1 + n

1

имеет предел при n → ∞.

Доказательство. Воспользуемся формулой бинома Ньютона:

(a + b)n = an +

n

an−1b +

n(n − 1)

an−2b2

+ ... + bn,

1!

2!

здесь k! = 1 · 2 · ... · k

(знак ! называется факториал), тогда

n

1! n

2!

n2

3!

n3

n

yn = 1 +

1

= 1 +

n

1

+

n(n − 1)

1

+

n(n − 1)(n − 2)

1

+ . . .

. . . +

n(n − 1) . . . (n − n + 1)

1

=

= 1 + 1 + 1

1 2 1 − n +

n!

nn

1 2 3 1 − n 1 − n + . . .

1

1

1

2

·

·

·

·

1 · 2 · . . . · n

− n

− n ·

−

n

. . . +

1

1

1

1

2

. . .

1

n − 1

.

(1)

Из последнего равенства следует, что последовательность

1

n

возрастает при

1 + n

возрастании n.

5

Действительно, при переходе от значения

n к значению n + 1 каждое слагаемое

последней суммы возрастает

< 1 · 2 1 − n + 1

и т. д.

1 · 2 1 − n

1

1

1

1

и добавляется еще один член. (Все члены разложения – положительны.)

последовательность yn

1

n

ограничена сверху. Заметим, что

Докажем, что

=1 1 + n

1

2

1 −

< 1;

1 −

1 −

< 1

и т. д.

n

n

n

Тогда заменив в (1) выражения стоящие в скобках единицей, получим неравенство

	1 + n			n							+ 1 · 2 · 3 + . . . + 1 · 2 · 3 · . . . · n .
				< 1 + 1 + 1 · 2
		1						1						1						1
Замечая, далее, что
	1	<		1	,			1			<	1		, . . . ,							1					<	1		,
1 · 2 · 3				22		1 · 2 · 3 · 4															1 · 2 · . . . · n						2n−1
											23
можем написать неравенство
			1 + n					n						2 +			22			+ ... + 2n−1 .
								< 1 + 1 +
						1									1		1						1

Члены, начиная со второго, правой части этого неравенства образуют геометрическую прогрессию со знаменателем q = 1/2 и первым членом a = 1, поэтому

n

< 1 +

1 + 2 +

22 + ... +

2n−1

=

1 + n

1

1

1

1

1

q

1

2

"

−

2

#

< 3.

= 1 + a − aqn = 1 + 1 −

21

n

= 1 + 2

1

n−1

−

−

1

Следовательно, для всех n получаем:

yn =

n

1 + n

< 3.

1

Последовательность

1 + 1

n

монотонно

возрастает

и

ограничена сверху,

n

1 она имеет предел. Этот предел обозначается e :

следовательно, по теореме

n

n→∞

n

lim

1 +

1

= e.

Число e иррациональное, приближенно оно равно 2, 718. Число e играет очень важную роль в математическом анализе.

Если в формуле

e = lim 1 + 1 n

n→∞ n

положить z = 1 , то она примет вид

n

1

e = lim(1 + z) z .

z→0

Оказывается, эта формула верна последовательность значений zn = нулю.

не	только тогда, когда переменная z пробегает
1 ,	но и при любом другом законе стремления z к
n

6