kurs_lekcii_mo_matematicheskomu_analizu / ПРямая и плоскость в пространстве

ТЕМА 12. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ.

1.Условие параллельности и перпендикулярности прямой и плоскости

Рассмотрим прямую L :
	x − x1	=	y − y1	=	z − z1
	m		n		p

и плоскость α :

Ax + By + Cz + D = 0.

Прямая L и плоскость α :

а) перпендикулярны друг другу тогда и только тогда, когда направляющий вектор

прямой

s

= (m, n, p) и нормальный

вектор

N = (A, B, C) плоскости коллинеарны, т.

е.

A

B

C

и

N ||

=

=

;

(8)

s

m

n

p

б) параллельны друг другу тогда и только тогда, когда векторы s = (m, n, p) и N =

(A, B, C) перпендикулярны, т. е.

(

Am + Bn + Cp = 0.

(9)

s, N ) = 0 и

Пример 1.

M1(2, −3, 4) параллельно

Написать уравнение плоскости, проходящей через точку

прямым

y − 1

z − 3

x + 1

y − 1

z + 5

x

=

=

и

=

=

.

1

2

2

8

4

0

Решение. Запишем уравнение связки плоскостей, проходящих через данную точку

M1 :

A(x − 2) + B(y + 3) + C(z − 4) = 0.

Так как искомая плоскость должна быть параллельна данным прямым, то ее нормальный вектор N должен быть перпендикулярен направляющим векторам s1 = i + 2j + 8k и

s2 = 4i + 0j + 2k этих прямых. Поэтому в качестве вектора N можно взять векторное произведение векторов s1 и s2 :

N = s1				s2 =								8		= 4i + 30j 8k.
						1			2
							i			j		k
			×			4			0			2						−

Следовательно, A = 4, B = 30, C = −8. Подставляя найденные значения A, B, C в уравнение связки плоскостей, получим

4(x − 2) + 30(y + 3) − 8(z − 4) = 0 или 2x + 15y − 4z + 57 = 0.

1

2.Точка пересечения прямой и плоскости

Пусть требуется найти точку пересечения прямой L :

	x − x1	=	y − y1	=	z − z1
	m		n		p

и плоскости α :

Ax + By + Cz + D = 0.

Запишем уравнение прямой в параметрическом виде (3):

x = x1 + mt,

y = y1 + nt,

z = z1 + pt.

Каждому значению параметра t соответствует точка прямой. Нужно выбрать такое значение t, при котором точка прямой будет лежать на плоскости. Подставляя значения x, y, z в уравнение плоскости, получим уравнение, из которого найдем значения параметра t :

A(x1 + mt) + B(y1 + nt) + C(z1 + pt) + D = 0, t(Am + Bn + Cp) = −(Ax1 + By1 + Cz1 + D),

t = −Ax1 + By1 + Cz1 + D . Am + Bn + Cp

Найденное значение t будет единственным в том случае, если прямая и плоскость не параллельны и, следовательно, направляющий вектор прямой s = (m, n, p) и нормальный вектор N = (A, B, C) плоскости не перпендикулярны, и их скалярное произведение не равно 0:

(N ,

s

) = Am + Bn + Cp 6= 0.

Значение t подставим в параметрические уравнения

прямой (3) и определим

координаты точки пересечения прямой и плоскости.

Пример 2.

Найти точку пересечения прямой

x − 1

=

y + 1

=

z − 5

и плоскости 2x+3y

−

2z +2 =

2

3

2

0.

Решение. Запишем уравнения данной прямой в параметрическом виде:

x = 2t + 1,

y = 3t − 1,

z = 2t + 5.

Подставим эти выражения для x, y, z в уравнение плоскости:

2(2t + 1) + 3(3t − 1) − 2(2t + 5) + 2 = 0 t = 1.

Подставим t = 1 в параметрические уравнения прямой. Получим

x = 2 · 1 + 1 = 3,

y = 3 · 1 − 1 = 2,

z = 2 · 1 + 5 = 7.

Итак, прямая и плоскость пересекаются в точке M (3, 2, 7).

2

3.Угол между прямой и плоскостью

6N

7

s

γ

ϕ

α

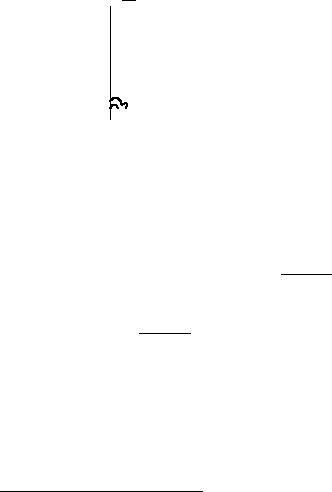
Пусть ϕ – угол между прямой

L и плоскостью α, а γ – угол между нормальным

вектором плоскости N и направляющим вектором прямой

s, тогда

π

(

(

s, N )

s, N )

cos γ = cos

± ϕ = ± sin ϕ =

;

sin ϕ =

|

|

;

2

s

s

N

N

|

| · |

|

|

| · |

|

ϕ = arcsin

|(

s, N )|

.

(10)

|

s

| · |N |

Пример 3.

x = 5 + t,

−

−

Найти угол между

прямой

−

3 + t,

и

плоскостью

4x

2y

2z

+ 7 = 0.

y =

z = 4 − 2t

Решение.

(10). Так как s

= (1

,

1

,

2)

,

N

= (4

,

2

,

2)

, то

Применяем формулу

−

−

−

sin ϕ =

|4 · 1 + (−2) · 1 + (−2) · (−2)|

=

6

=

1

.

√

√

√ √

2

1 + 1 + 4 16 + 4 + 4

6 24

Следовательно, ϕ = 30o .

4.Пучок плоскостей

Совокупность всех плоскостей, проходящих через заданную прямую L, называется

пучком плоскостей, а прямая L – осью пучка.

Пусть ось пучка задана уравнениями (1)

A1x + B1y + C1z + D1 = 0,

A2x + B2y + C2z + D2 = 0.

Почленно умножим второе уравнение системы (1) на постоянную λ и сложим с первым уравнением:

A1x + B1y + C1z + D1 + λ(A2x + B2y + C2z + D2) = 0.

(11)

Уравнение (11) имеет первую степень относительно x, y, z и, следовательно, при любом численном значении λ определяет плоскость. Так как (11) есть следствие уравнений (1), то координаты точки, удовлетворяющие уравнениям (1), будут удовлетворять и

3

уравнению (11). Следовательно, при любом численном значении λ уравнение (11) есть уравнение плоскости, проходящей через прямую (1).

Уравнение (11) есть уравнение пучка плоскостей.

Пример 4.

Найти уравнение плоскости, проходящей через прямую

2x + 3y − 5z + 1 = 0, 3x − y + z + 28 = 0

и точку M1(1, −2, 3).

Решение. Запишем уравнение пучка плоскостей, проходящих через данную прямую:

2x + 3y − 5z + 1 + λ(3x − y + z + 28) = 0.

Подставив в уравнение пучка координаты точки M1 , найдем значение λ :

2 · 1 + 3 · (−2) − 5 · 3 + 1 + λ(3 · 1 − 1 · (−2) + 3 + 28) = 0 λ = 12 .

Подставив λ = 12 в уравнение пучка, получим уравнение искомой плоскости:

2x + 3y − 5z + 1 +	1	(3x − y + z + 28) = 0	или 7x + 5y − 9z + 30 = 0.
	2

Пример 5.

Найти точку, симметричную точке P (2, 7, 1) относительно плоскости x−4y+z+7 = 0. Решение. Искомая точка Q является вторым концом отрезка P Q, для которого серединой будет точка R – проекция точки P на данную плоскость. Найдем точку R. Уравнения прямой, перпендикулярной к данной плоскости и проходящей через точку P ,

имеют вид

x = 2 + t,

y = 7 − 4t,

z = 1 + t.

Точка R является точкой пересечения полученного перпендикуляра и данной плоскости.

Подставляя выражения	для x, y, z в уравнение плоскости, получаем
(2	+ t) − 4(7 − 4t) + (1 + t) + 7 = 0 t = 1.

Подставим t = 1 в параметрические уравнения прямой и получим координаты точки R

y = 7		4			1 = 3,				R(3, 3, 2).
	x = 2 + 1 = 3,
		−		·
	z = 1	+ 1		= 2
По формулам деления отрезка пополам:
x =	x1 + x2		, y =			y1 + y2		, z =		z1 + z2	,
2					2				2

которые в данном случае целесообразно представить в виде

x2 = 2x − x1, y2 = 2y − y1, z2 = 2z − z1,

находим

x2 = 2 · 3 − 2 = 4, y2 = 2 · 3 − 7 = −1,

z2 = 2 · 2 − 1 = 3,

т.е. координаты точки Q(4, −1, 3) .

4