gos / Гетманов2

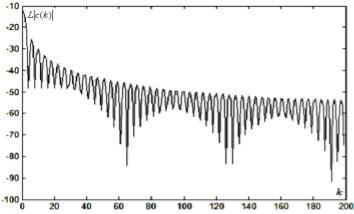
y(i) 1 для 0 i N0 1,

y(i) 0

для N0 i N 1. (4.1.12)

Нахождение ДПФ для данного сигнала сводится к суммированию комплексной геометрической прогрессии со знаменателем W k :

N0 1

kN

kN0

kN0

KN0

1

1 1 W

0

1 W

2

W 2 W

2

c(k)

1 W ki

,

N

N 1 W k

N

k

k

k

i 0

W 2 W

W

2

2

k 0, 1,...,

N 1.

Cделаем необходимые выкладки, чтобы получить формулы для значений амплитудного и фазового спектров

1 W

kN0

kN0

W

kN0

k

kN0

sin

N0k

2

W 2

2

1

N

W 2

2

,

N W

2

W 2

W 2

N

sin k

k

k

k

N0k

N

1

sin

2 k

kN0

N

с(k)

N

k

, (k)

(1

N0 )k ,

2

2

N

N

sin N

k 0, 1,...,

N 1.

(4.1.13)

Для расчётов c(k)

по формулам (4.1.13)

взяты значения N 512,

N0 126. На рис. 4.1.1 изображен логарифмический амплитудный

сигнала (4.1.12) для точек k 0, 1,..., 199.

спектр ДПФ L

c(k)

Рис. 4.1.1. Логарифмический амплитудный спектр ДПФ для прямоугольного импульса

117

В практике обработки дискретных наблюдений, как правило, приходится иметь дело с действительными сигналами. Однако многие программы алгоритмов вычисления коэффициентов ДПФ ввиду определённых удобств записываются в комплексной форме. Чтобы можно было воспользоваться этими программами для вычисления ДПФ действительных сигналов, необходимо положить в комплексных наблюдениях мнимую составляющую, равную нулю:

y(i) y1(i) j 0,

y2 (i) 0,

i 0, 1,..., N 1.

Для комплексного сигнала с нулевой мнимой составляющей проведём вычисления коэффициентов ДПФ, получим

		1	N 1		2			1	N 1	2
	c1(k)		y1	(i)cos		ki, c2	(k)		y1(i)sin		ki,
		N i 0			N			N i 0		N
				k 0, 1,...,			N 1.

Коэффициенты комплексного и действительного ДПФ связаны простыми соотношениями, которые следует применять для пересчёта:

a k 2c1 (k) ,

k 0,1,..., N 1,

bk 2c2 (k) , k 1,..., N 1.

4.2. Свойства дискретного преобразования Фурье

4.2.1. ДПФ для комплексной экспоненциальной функции

Необходимость вычисления дискретного преобразования Фурье для комплексной экспоненциальной функции может возникать для многих задач ЦОС.

Комплексная экспоненциальная функция определяется в дис-

кретных точках i 0, 1,..., N 1 с помощью формулы
y(i) Ae j(2 f Ti ) ,	(4.2.1)

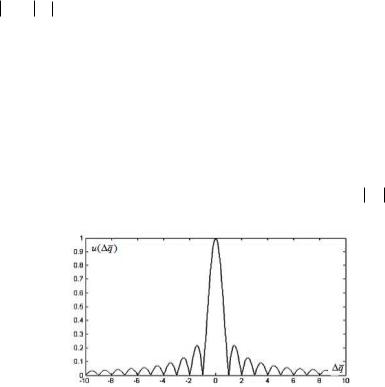
где A – амплитуда; f – частота, Гц; – начальная фаза; T – интервал дискретизации; NT – длительность интервала наблюдения. Величина T0 1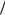 f является периодом рассматриваемой функции. Возможно

представление (4.2.1) в эквивалентном виде:

y(i) Acos(2 f Ti ) j sin(2 fTi ),

i 0, 1,..., N 1.

Вычисление ДПФ для (4.2.1) может быть реализовано на основе суммирования с применением табличных тригонометрических формул

118

cc((kk)) cc((kk)) jcjc

((kk))

11

22

1

N 1

2

2

=

( Acos(2 f Ti ) jAsin 2 f Ti cos

ki j sin

ki ,

N i 0

N

N

1

N 1

2

2

c1

(k)

Acos(2 f Ti )cos

ki Asin(2 fTi )sin

ki ,

N i 0

N

N

1

N 1

2

2

c2

(k)

Acos(2 fTi )sin

ki

Asin(2 f Ti )cos

ki .

N i 0

N

N

Вычисление ДПФ для комплексной экспоненциальной функции может быть произведено с помощью суммирования специально сформированной геометрической прогрессии. Введём параметр q, равный числу периодов функции (4.2.1), укладывающихся на интервале наблюдения, и приведём очевидные равенства

q	NT		NT	f NT ,	f T	q	,	2 f Ti	2	qi,	e j2 fTi W qi .
	T0		1 / f			N			N

Функция (4.2.1) может быть записана с учётом последнего равенства следующим образом:

y(i) Ae j(2 fTi ) Ae j e j 2 fTi Ae j W qi , i 0, 1,..., N 1. (4.2.2)

Для y(i) в форме (4.2.2) нахождение коэффициентов с(k) ДПФ сводится к вычислению суммы N членов комплексной геометрической прогрессии со знаменателем W q k

				1	N 1
		с(k)			Ae j W qiW ki
				N i 0
	1	N 1		1		1 W (q k ) N
		Ae j W (q k )i			Ae j		, k 0, 1,..., N 1.
	N			N		1 W q k
		i 0

Воспользуемся приёмом, который был ранее использован в (4.1.12), сделаем необходимые преобразования для с(k) :

(q k ) N

(q k ) N

с(k)

1

Ae j

1 W

1

Ae j

W

2

N

1 W q k

N

q k

W 2

Получим амплитудные с(k) и фазовые (k)

ного ДПФ, k 0, 1,..., N 1:

W	(q k ) N				W	(q k ) N
			2			2			.
	W		q k		W	q k
				2		2

зависимости для дан-

119

c(k)

A

W

(q k ) N

(q k ) N

2

W

2

N

q k

q k

W

2

W 2

A

sin

2 (q k)N

A

sin (q k)

N

2

,

(4.2.3)

N

sin

2

(q k)

N

sin (q k)

N

2

N

(q k ) N

q k

2 (q k)N

2

(q k)

(k) arg W

2

arg W

2

N

2

N

2

(q k)

N 1

.

(4.2.4)

N

Вычисление

модулей

нормированных

коэффициентов

ДПФ

c0 (k) c(k) N удобно проиллюстрировать с помощью аппаратной

функции u( q, q0

, k),

которая образуется

на основе (4.2.3):

u( q, q0 , k)

1

sin (q0

q k)

, k 0, 1,...,

N 1,

N

sin

(q

q k)

N

0

q .

На рис. 4.2.1 изображён график аппаратной функции

u( q) при

q0 k,

N 512

и переменная q удовлетворяет

неравенству

10 q 10. Нетрудно убедиться в том, что аппаратная функция быстро уменьшается с ростом q; так, при q 10 и q N значения функции u( q) 0,05 становятся существенно малыми.

Рис. 4.2.1. График аппаратной функции

120

Аппаратная функция может быть представлена в зависимости от частотного параметра f в виде u( f ); очевидно, для f 10 f , где f – шаг дискретности по частоте, должно выполняться неравенство u( f ) 0,05.

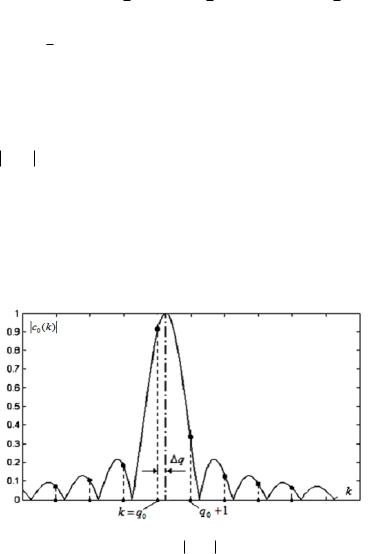
На рис. 4.2.2 помещён график для вычисления нормированных

коэффициентов ДПФ		c0 (k)	, для примера взяты численные значе-
ния N 512, q0 4,	q 0,25. На этом графике представлена ап-

паратная функция, смещённая вправо на величину q0 q. Значения c0 (k) отмечены жирными точками и пунктирными линиями,

которые соответствуют целочисленным k. Ясно, что максимальное значение модуля коэффициента ДПФ приходится на номер k q0.

Очевидно, что при				q 0 и k q0 4 модуль коэффициента ДПФ
	с(4)		1; для k 4		с0 (k)		0 – все остальные модули коэффициен-

тов ДПФ равняются нулю. Для q0 4 имеет место						с0 (4)		1 и для
k 4 выполнятся условие		с0 (k)		0.

Рис. 4.2.2. График для вычисления нормированных коэффициентов ДПФ c0 (k)

В том случае, когда комплексная синусоида укладывается почти целое число периодов на интервале наблюдения, примерно равное q0 , амплитудный спектр ДПФ сосредоточен в области значений k,

121

близких к q0 ; вне этой области амплитудный спектр ДПФ является

почти нулевым. Для случаев, когда комплексная синусоида не укладывается целое число периодов на интервале наблюдения, амплитудный спектр ДПФ является «размазанным».

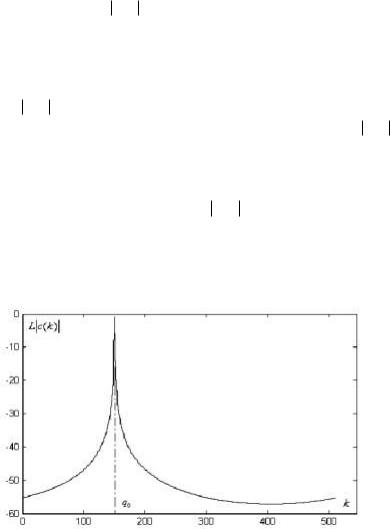
Рассмотрим вид зависимости амплитудного спектра ДПФ – модулей коэффициентов с(k) от дискретного номера k для комплексной экспоненциальной функции. Для (4.2.1) зададим А 1, f 29,4 Гц, 0,5, N 512, T 0,01 c; для данной функции параметр q NTf 150, 25, q0 150, q 0,25. На рис. 4.2.3 изображён график амплитудного спектра ДПФ в логарифмическом масштабе L c(k) , k 0, 1,..., N 1. Шаг дискретности по частоте спектра составляет величину f 1/ NT 0,1953 Гц. Значениям L c(k)

могут быть	поставлены	в соответствие дискретные	частоты
fk f k [Гц],	k 0, 1,...,	N 1, которые изменяются в	диапазоне

0 fk fN 1.

Из рис. 4.2.3 следует, что график L c(k) содержит резкий спектральный максимум в области k q0 : в указанной области со-

средоточены основные значения амплитудного спектра, вне области значения амплитудного спектра пренебрежимо малы. На основе графика амплитудного спектра может быть произведена оценка

Рис. 4.2.3. Амплитудный спектр ДПФ комплексной экспоненциальной функции в логарифмическом масштабе

122

параметров комплексной экспоненциальной функции. По значению номера k , соответствующего спектральному максимуму на графи-

ке рис. 4.2.3,

k arg{ min
	L	c(k)	}
0 k N	1

и в предположении малого значения q, оценивается частота f и амплитуда A исходной экспоненциальной функции. В данном случае k 150 и можно считать, что с некоторой погреш-

ностью f fk	29,295 Гц и	А	с(k )	,	L	c(k )	1,5 Дб,

с(k ) 10 1,5/20 0,8411 . Максимальная погрешность оценки час-

тоты составляет величину f			f / 2 0,0977 Гц. Максимальная
погрешность амплитуды определяется формулой
A		A	1	sin / 2			,
		N		sin
					2N
и при N 512 принимает	значение				A 0,38. Разумеется, при

q 0 величины данных погрешностей стремятся к нулю.

С использованием (4.2.4) можно заключить, что оценка начальной фазы

(k ) (q k) N 1,

N

и для случая q 0 близка к значению начальной фазы .

4.2.2. Элементарные свойства ДПФ

Рассмотрим некоторые простейшие свойства ДПФ, которые будут использованы в дальнейшем.

1. ДПФ является линейной операцией. Пусть дискретная последо-

вательность z(i)	образуется как	сумма последовательностей
x(i), y(i) , i 0, 1,..., N 1, с весами		, и известны ДПФ этих по-
следовательностей:	cх (k), cy (k),	k 0, 1,..., N 1. Тогда ДПФ

сz (k) для последовательности z(i) представляет собой взвешенную сумму ДПФ cx (k), cy (k) :

123

z(i) x(i) y(i), i 0, 1,..., N 1, сz (k) cx (k) cy (k),

k0, 1,..., N 1.

2.Благодаря особенностям ДПФ от комплексной экспоненциальной функции и свойству линейности с использованием ДПФ оказывается удобным производить анализ многочастотных сигналов. Пусть наблюдаемый сигнал представляет собой сумму нескольких синусоид с частотами, которые различаются в достаточной степени. Тогда амплитудный спектр ДПФ такого сигнала содержит набор спектральных максимумов: количество спектральных максимумов равняется числу частотных составляющих в сигнале, а частотные координаты и высоты спектральных максимумов определяются частотами и амплитудами составляющих. На основе амплитудного спектра ДПФ возможно приближённое решение достаточно сложной задачи оценивания параметров многочастотных сигналов.

Проведём вычисления ДПФ для суммы трёх комплексных экспоненциальных функций с различными частотами

		3
	y(i) As e j(2 fsTi s ) , i 0, 1,..., N 1.				(4.2.5)
		s 1
Для (4.2.5) примем значения			параметров	A1 0,5;	f1 14,6 Гц;
1 1,0;	A2 1,0;	f2 29,4 Гц;	1 0,5 и	A3 1,5;	f1 48,76 Гц;
1 1,5;	N 512;	T 0,01 c; f 1/ NT 0,1953 Гц. На рис. 4.2.4

Рис. 4.2.4. Амплитудный спектр ДПФ для трехчастотной комплексной функции

124

изображён логарифмический амплитудный спектр ДПФ трёхчастотной комплексной функции (4.2.5). Видно наличие в нём трёх спектральных максимумов, соответствующих частотам f1, f2 и f3.

По виду графика L c(k) рис. 4.2.4 определяются положения спектральных максимумов k1 74, k2 150, k3 249, на основе ко-

торых

оцениваются

соответствующие

частоты

fs fks ;

s = 1, 2, 3; f1 0,1953 74 14,45 Гц;

f21 0,1953 150 29,29 Гц;

f3 0,1953 249 48,63 Гц и

логарифмические

амплитуды

L

c(k1 )

7 Дб;

L

c(k2 )

1 Дб;

L

c(k3 )

20 Дб.

После пере-

счёта

получаются

оценки

амплитуд

А 10 7/20 0,447;

1

А2 10 1/20 0,891; А3 10 20/20 0,1. В силу различия в достаточной степени частот f1 f3 амплитудный спектр ДПФ для подобной

трехчастотной функции может представляться в виде суммы амплитудных спектров ДПФ составляющих.

3. Воспользовавшись свойством линейности можно вычислить ДПФ действительной косинусоидальной (синусоидальной) функции

y(i) cos2 f Ti,	i 0, 1,..., N 1. Приведём известные соотношения
W qi e j2 fTi	cos2 f Ti j sin 2 f Ti, q NTf , W Ni 1,
		W qi W	qi		W qi W ( N q)i
cos 2 f Ti						.	(4.2.6)
		2			2

Из (4.2.6) следует, что ДПФ для функции y(i) cos2 f Ti представ-

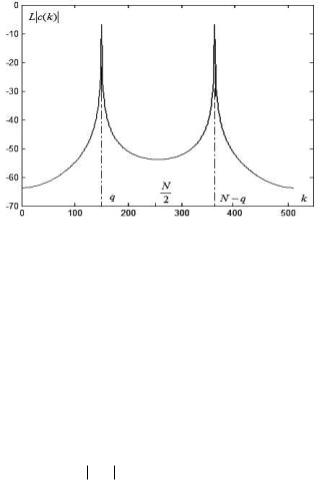
ляет собой сумму ДПФ для комплексных экспоненциальных функций с параметрами q и (N q). На рис. 4.2.5 изображён логарифми-

ческий амплитудный ДПФ-спектр для косинусоидальной функции y(i) cos2 fTi.

Анализируя график рис. 4.2.5 можно сделать вывод, что ДПФ косинусоидальной функции состоит из двух составляющих, симметричных относительно точки N/2.

4. Рассмотрим влияние сдвигов при вычислении ДПФ. Пусть задана последовательность y(i), i 0, 1,..., N 1. Продолжим эту по-

следовательность с периодом N. Осуществим сдвиг данной последовательности на i0 единиц, образуем новую последовательность

z(i) y(i i0 ). Вычислим коэффициенты ДПФ для последовательности z(i), с учётом периодичности

125

		1	N 1	1	N 1
	сz (k)		y(i i0 )W ki		y(i i0 )W k (i i0 )W ki0	W ki0 cу (k).
		N i 0		N i 0

Рис. 4.2.5. Амплитудный спектр ДПФ для косинусоидальной функции

Справедливо и обратное утверждение. Если z(i) W k0i y(i), тогда c помощью почти аналогичных выкладок получим

	1	N 1		1		N 1
сz (k)		W k0i y(i)W ki				y(i)W (k k0 )i cy (k k0 ).
	N i 0			N i 0
5. Коэффициенты ДПФ			c(k)			можно рассматривать для

k . Тогда можно утверждать, что c(k) периодичны по k с периодом N. В самом деле

		1	N 1	1	N 1
	c(k)		y(i)W ki		y(i)W ( k N )i c(k N ).
		N i 0		N i 0

6. Установим для действительных последовательностей модулей коэффициентов ДПФ с(k) свойство симметрии относительно точки

k N /2. Положив мнимую составляющую наблюдений y2 (i) 0, представим выражения для действительной и мнимой частей ДПФ:

		1	N 1	2			1	N 1	2
	c1(k)		y1(i)cos		ki,	c2 (k)		y1(i)sin		ki.
		N i 0		N			N i 0		N

Запишем очевидные равенства

126