gos / Гетманов2

На основе системы модельных сигналов (4.4.16) произведены вычисления оценки функции коэффициента когерентности xy (k).

На рис. 4.4.2а приведён график оценки xy (k), соответствующий m 32; 1 1,5; 2 1,5, – расчётный пример 1.

Рис. 4.4.2а. Оценка коэффициента когерентности модельных сигналов (4.4.16) – пример 1

На рис. 4.4.2б приведён график оценки xy (k), соответствующий m 32; 1 7,5; 2 7,5, – расчётный пример 2 с увеличен-

ной дисперсией шумов. На рис. 4.4.2в приведён график оценкиxy (k) параметров m 64; 1 7,5; 2 7,5, – расчётный пример

3 с увеличенным числом локальных интервалов.

Рис.4.4.2б. Оценка коэффициента когерентности модельных сигналов (4.4.13) – пример 2

157

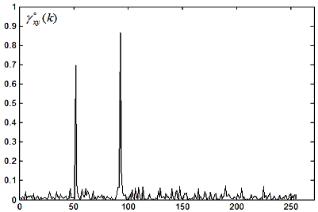
Рис.4.4.2в. Оценка коэффициента когерентности модельных сигналов (4.4.13) – пример 3

Введённая эмпирическим путём функция коэффициента когерентности является чувствительным индикатором наличия связей между сигналами.

4.5. Алгоритм быстрого преобразования Фурье

Оценим временные затраты, необходимые для вычисления коэффициентов дискретного преобразования Фурье (ДПФ) для последовательности данных y(i), i 0, 1,..., N 1, непосредственно

по формулам из определения. Запишем ещё раз выражение для прямого ДПФ, включающее в себя операции сложения, умножения и вычисления тригонометрических функций:

		1	N 1
	c(k)		y(i)W ki ,	k 0, 1,..., N 1.
		N i 0

Если предположить, что в памяти ЭВМ заранее сформирована таблица значений базисных синусоидальных функций W ki , а также справедливо соотношение для времени выполнения операций комплексного сложения tc и умножения ty в виде неравенства tc ty ,

то время вычисления N комплексных коэффициентов ДПФ приближённо оценивается по формуле

158

T	N 2t	y	.	(4.5.1)
ДПФ

Временные затраты вычисления коэффициентов дискретного преобразования Фурье на основании определения растут пропорцио-

нально N 2 и для больших N составляют значительную величину.

Предлагаемый алгоритм быстрого преобразования Фурье (БПФ) обеспечивает существенное снижение временных затрат вычис-

ления коэффициентов ДПФ. Однако применение этого алгоритма возможно только для некоторых значений N; здесь будет рассмот-

рен вариант алгоритма БПФ для N 2r – числа наблюдений, равного целой степени двойки. В основе предлагаемого алгоритма БПФ лежит возможность сведения вычисления ДПФ для N чисел к вычислению двух ДПФ для N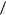2 чисел с проведением дополни-

тельных операций умножения.

Рассмотрим снова выражение для вычисления коэффициентов ДПФ; опустим для дальнейших удобств выкладок множитель 1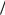 N , который можно будет учесть на последнем шаге:

N 1
c(k) y(i)W ki ,	k 0, 1,..., N 1.
i 0

Разобьём последовательность y(i), i 0, 1,..., N 1, на две подпос-

ледовательности с чётными и нечётными номерами входных данных:

g(s) y(2s), h(s) y(2s 1), s 0, 1,..., N2 1.

Коэффициенты ДПФ исходной последовательности могут быть записаны в виде двух сумм, k 0, 1,..., N 1:

	N /2 1		2		N /2 1		j	2	k (2s 1)
с(k)	g(s)e	j N k 2s			h(s)e			N			.
	s 0				s 0
Сформируем указанные суммы в виде ДПФ размерности N 2 :
N /2 1			2		2	N /2 1				2
с(k)	g(s)e j			ks e j N k		h(s)e j					ks .
			N /2							N /2
	s 0					s 0

Обозначим коэффициенты ДПФ cg (k), ch (k) для введённых чётных и нечётных подпоследовательностей:

159

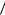
N /2 1

2

N /2 1

2

сg (k) g(s)e j

ks ,

сh (k)

h(s)e j

ks ,

N /2

N /2

s 0

s 0

k 0,

1,....,

N 2 1.

Запишем,

введя

множитель

W k ,

первые N /2

коэффициентов

N

ДПФ с(k) :

W k

e

j

2

с(k) c

(k) W

k c (k),

k 0, 1,..., N /2 1.

N ,

g

N

N

h

Eсли осуществить сдвиг индекса k на N /2, то оставшиеся коэффициенты ДПФ исходной последовательности с номерами от N /2 до N /2 1 записываются аналогично:

WN (k N /2) WN k , с(k N /2) cg (k) WN k ch (k), k 0, 1,..., N /2 1.

Из приведённого рассмотрения следует, что нахождение ДПФ для последовательности из N чисел свелось к вычислению двух ДПФ для двух подпоследовательностей из N /2 чисел и N /2 операций

комплексных умножений.

Вычисление ДПФ можно реализовать пошагово. На предпоследнем шаге можно осуществить переход к вычислению ДПФ для подпоследовательностей из N /2 чисел через ДПФ для подпосле-

довательностей из N /4 чисел и т.д. Общее число шагов подобного алгоритма составляет значение показателя степени двойки

r log2 N.

Проанализировав структуру формул алгоритма вычисления ДПФ из N чисел через вычисление ДПФ для подпоследовательностей из N /2 чисел, можно заметить, что алгоритм распадается на

последовательность однотипных подалгоритмов. Действительно, выделим типовой подалгоритм

с(k) c	g	(k) W k c (k),	с(k N /2) c	g	(k) W k c (k),
		N h			N h
		k 0, 1,..., N /2 1.			(4.5.2)

Указанный подалгоритм называется «бабочка»; граф «бабочки» – схематическое изображение вычислительных операций, соответствующих (4.5.2) представлен на рис. 4.5.1.

160

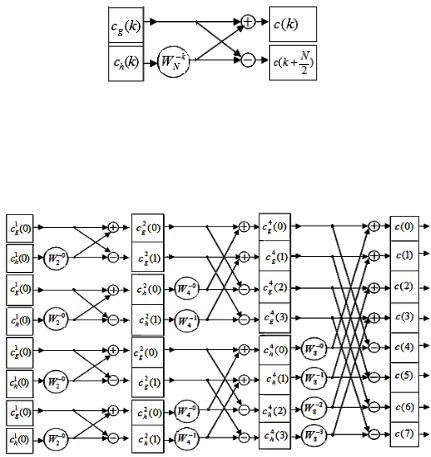
Рис. 4.5.1. Граф операции «бабочка»

Комбинации однотипных «бабочек» при вычислении коэффициентов ДПФ составляет основу алгоритма БПФ. На рис. 4.5.2 представлен в качестве примера граф алгоритма БПФ для N 8, состоящий из трёх шагов.

Рис. 4.5.2. Граф алгоритма БПФ для N 8

Для удобств рассмотрений введены индексы для промежуточ-

ных коэффициентов ДПФ сN /2	(k),	сN /2	(k); показатель	N /2 опре-
g		h

деляет размерности ДПФ, реализуемых на соответствующем шаге работы алгоритма.

Чтобы предлагаемый алгоритм БПФ начал работать, необходима всего лишь предварительная перетасовка входных данных во временной области. Работу алгоритма перетасовки, в соответствии с разработанным графом рис. 4.5.2, удобно анализировать с право-

161

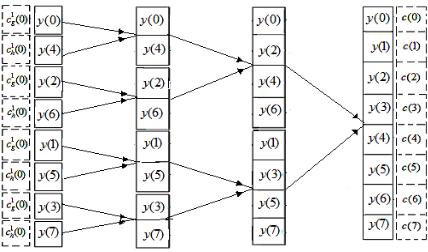
го конца (от конца к началу), что приллюстрировано на диаграмме рис. 4.5.3.

Оценим временные затраты, необходимые для работы алгоритма БПФ. На каждом шаге алгоритма БПФ выполняется N /2 опера-

ций «бабочка»; в каждой «бабочке» реализуется только одно комплексное умножение, поэтому временные затраты на каждом шаге предлагаемого алгоритма приближённо составляют величину N /2 ty . Число шагов в алгоритме БПФ уже было подсчитано ра-

нее; поэтому время вычисления N коэффициентов дискретного преобразования Фурье по предлагаемому алгоритму БПФ представится следующей оценкой

TБПФ N /2ty log2 N.

(4.5.3)

Рис. 4.5.3. Перетасовка входных данных для алгоритма БПФ с N 8

Определим возможный выигрыш во времени по предлагаемому алгоритму БПФ по сравнению с вычислением ДПФ на основе фор-

мул (4.5.1) и (4.5.3):

	T		N 2t	y		2N
	ДПФ						.
	ТБПФ		(N / 2)ty log2 N			log2 N

Имеем следующие значения введённого показателя эффективности:

N 512,	9 113,	N 1024,	10 204,	N 8192,	13 1203. Из
			162

полученных оценок выигрышей следует, что алгоритм БПФ радикально уменьшает временные затраты при вычислении ДПФ.

Список вопросов для самопроверки к гл. 4

1.В чём состоит формулировка задачи аппроксимации дискретных наблюдений сигналов полигармоническими моделями и каковы особенности её решения?

2.В чём состоят особенности задачи аппроксимации дискретных наблюдений сигналов на основе моделей, линейных по части параметров?

3.В чём состоит формулировка задачи аппроксимация дискретных наблюдений сигналов на основе дискретного преобразования Фурье для действительного случая?

4.В чём состоит формулировка задачи аппроксимация дискретных наблюдений сигналов на основе дискретного преобразования Фурье для комплексного случая?

5.В чём состоит алгоритм вычисления дискретного преобразования Фурье для комплексной синусоиды?

6.В чём состоит определение для разрешающей способности ДПФ?

7.Какие свойства дискретного преобразования Фурье приведены в разд. 4.2?

8.В чём заключается формулировка теоремы Парсеваля для случая непрерывных сигналов?

9.Каким образом реализуется вывод теоремы Парсеваля для случая дискретных сигналов?

10.В чём состоит определение для функции спектральной плотности мощности сигналов (СПМ)?

11.Каким образом реализуется вывод оценки функции СПМ для стационарных эргодических дискретных сигналов?

12.Для каких целей применяются временные окна?

13.Каким образом реализуется алгоритм вычисления оценок параметров сигналов на основе функции СПМ?

14.Каким образом определяется функция взаимной спектральной плотности мощности сигналов (ВСПМ)?

15.Каким образом реализуется алгоритм вычисления оценок разностей фаз на основе функции ВСПМ?

163

16.Каким образом реализуется алгоритм вычисления оценок передаточных функций линейных систем на основе функции ВСПМ?

17.Каким образом реализуется алгоритм вычисления оценок функции когерентности на основе функций СПМ и ВСПМ?

18.Каким образом реализуется алгоритм быстрого преобразования Фурье (БПФ)?

Список задач к гл. 4

1. Вычислить коэффициенты ДПФ ck ,

если

1

N 1

y(i), i 0, 1,...,

N 1,

сk

y(i)W ki ,

k 0, 1,..., N 1,

N i 0

для заданных временных дискретных последовательностей:

1)

y(i) Ae j(2 f0Ti ) ;

y 0, 1,..., N 1;

k 0, 1,..., N 1;

2)

y(i) Acos(2 f0Ti );

i 0, 1,...,

N 1;

k 0, 1,..., N 1;

3)

y(i) Asin(2 f0Ti );

i 0, 1,...,

N 1;

k 0, 1,..., N 1;

i 0,...,

0

1;

1,

N

k 0, 1,...,

N 1;

4)

y(i)

0,

i N0 ,..., N 1,

0

5)

1,

i i

;

k 0, 1,..., N 1;

y(i)

i 0,..., i0

1,

i0 1,..., N 1,

0,

1

2

1;

1,

i N ,..., N

k 0, 1,..., N 1;

6)

y(i)

i 0,...,

N1 1,

i N2 ,...,

N 1,

0,

7)

y(i) Ae Ti ;

i 0, 1,..., N 1; k 0, 1,...,

N 1;

8)

y(i) Ae Ti ;

cos(2 fTi ); i 0, 1,..., N 1; k 0, 1,..., N 1;

Asin(2 f0Ti ),

i 0,..., N0 1;

,

k

0, 1,..., N 1;

9. y(i)

i N0 ,...,

N 1,

0,

10)

Asin(2 f0Ti),

i N1,...,

N2 1;

k 0, 1,..., N 1;

y(i)

i 0,...,

N1 1, i N2 ,...,

N 1,

0,

11)

y(i) Ti;

i 0,

1,..., N 1;

k 0, 1,...,

N 1;

12)

y(i) x(i) z(i);

k 0, 1,...,

N 1

13)

y(i), i 0, 1,...,

N 1,

y(i) y(i i0 ),

k 0, 1,..., N 1;

164

14) y(i), i 0, 1,..., N 1,

y(i) y(i)e j( Ti ) ,

k0, 1,..., N 1;

15)y(i) x(i)z(i), k 0, 1,..., N 1.

2. Определить характеристики разрешения составляющих двухчастотного сигнала на основе ДПФ

	y(Ti) A1 cos 2 f1Ti A2 cos 2 f2Ti, i 0, 1,..., N 1.
1.	Разрешимы ли составляющие сигнала с параметрами: A1 1,0;
A2 1,5; f1		5 Гц; f2 5,5 Гц; T 0,01 c; N 512?
2.	Разрешимы ли составляющие сигнала с параметрами:
A1 1,0; A2 1,5; f1 5 Гц;			f2 10,5 Гц; T 0,01 c; N 512?
3.	Для	параметров	сигнала:	A1 1,0; A2 1,5;	f1 5 Гц;
f2 5,5 Гц;		T 0,01 c, какое необходимо задать N для обеспече-
ния разрешения составляющих?
4.	Для	параметров	сигнала:	A1 1,0; A2 1,5;	f1 5 Гц,

f2 5,5 Гц, какой необходимо задать интервал наблюдения NT для

обеспечения разрешения составляющих?
5. Для параметров cигнала: A1 1,0;	A2 1,5;	f1 5 Гц и ин-

тервала наблюдения NT 4 c, какое минимальное значение частоты f2 может обеспечить разрешение составляющих?

165