gos / Гетманов2

2

N

2

N

2

N

cos

k i cos

k

i,

sin

k i

N

2

N

2

N

2

=sin

2 N

k

i,

N

2

из которых следует свойство симметрии

N

N

N

N

с1

k

c1

k ,

с2

k

c2

k

,

2

2

2

2

N

N

c

k

c

k

.

2

2

При анализе действительных сигналов вполне оправданно рассмотрение амплитудных спектров ДПФ для точек k 0, 1,..., N /2 1.

Аналогичным образом может быть установлено свойство центральной симметрии для фазовых углов ДПФ (k) относительно точки k N /2.

4.2.3. Разрешающая способность ДПФ

Амплитудный спектр ДПФ для многочастотных сигналов в общем случае, с учётом некоторых упрощающих предположений, состоит из набора спектральных максимумов. С помощью оценивания параметров амплитудного спектра ДПФ возможно решение многих задач анализа сложных колебательных сигналов.

Однако в ряде случаев проведение анализа сигналов на основе амплитудного спектра ДПФ сопряжено с рядом проблем. Эффективность анализа сигналов зависит, в частности, от разрешающей способности ДПФ-возможности различения на амплитудном спектре ДПФ спектральных максимумов составляющих для многочастотных сигналов с близкими частотами.

Рассмотрим пример двухчастотного действительного сигнала

y(i) A1 cos(2 f1Ti 1) A2 cos(2 f2Ti 2 ),			i 0, 1,..., N 1. (4.2.7)
с параметрами A1 1; A2 1,5;	1 0,5;	2	0,8; Т 0,01. Для

(4.2.7) f1 20 Гц, f2 20,06 Гц – частоты составляющих. Для рассматриваемого двухчастотного сигнала разность частот для составляющих принимает значение f1 f2 0,06 Гц. Для (4.2.7) вычис-

127

лим ДПФ при различных вариантов величин интервалов наблюдений. Вид амплитудного спектра зависит от разности частот f1, f2 и

шага дискретности спектра по частоте и особенностей аппаратной функции.

На рис. 4.2.6а изображены результаты вычисления логарифмиче-

ского амплитудного спектра	L		c( fk )		для N1 512 2 1024 и
длины интервала наблюдения,	составляющей 10,24 c . Кружками

Рис. 4.2.6а. Логарифмический амплитудный спектр ДПФ двухчастотного сигнала, f1 0,0976 Гц

Рис. 4.2.6б. Логарифмический амплитудный спектр ДПФ двухчастотного сигнала, f2 0,0031 Гц

128

отмечены восемь значений L c( fk ) с шагом дискретностиf1 1/ N1T 0,0976 Гц,для k 201 208, соответствующих часто-

там 19,62 20,30 Гц .

В данном случае		f1 f2		f1, (		f1 f2		/ f1 0,62 – расстоя-

ние по частоте между составляющими сигнала меньше шага дискретности спектра. В силу указанных неравенств на данном амплитудном спектре принципиально не могут быть видны раздельно составляющие сигнала – частотные составляющие в сигнале не разрешимы на основе ДПФ с f1 0,0976 Гц.

Для повышения разрешающей способности ДПФ производится увеличение временного интервала наблюдения. На рис. 4.2.6б изображены результаты вычисления логарифмического амплитудного спектра L c( fk ) для N2 512 64 32768; длина временного интер-

вала наблюдения и дискретность спектра по частоте составляют

327,68 c				и f2	1 / N2T 0,0031 Гц.					Поскольку в данном случае
	f1 f2			f2	(		f1 f2		/ f2 19,35),	то в силу указанных нера-

венств амплитудный спектр ДПФ состоит из двух отчётливо видимых раздельно спектральных максимумов – две частотные составляющие в сигнале разрешимы на основе ДПФ с f2 0,0031 Гц .

Разрешающая способность ДПФ определяется величинойf 1/ NT , которая совпадает с шагом дискретности по частоте ам-

плитудного спектра. Если обратиться к (4.2.7) и учесть свойства аппаратной функции, то спектр первой составляющей сосредоточен около частоты f1 и для частот fk , удовлетворяющих неравенству

fk f1 10 f , спектр первой составляющей становится сущест-

венно малым. Аналогично, для второй составляющей спектр сосредоточен около частоты f2 и для частот дискретных fk , удовлетво-

ряющих неравенству fk f2 10 f , спектр второй составляющей

становится существенно малым.

Общее правило приближённого определения разрешимости составляющих сигнала с близкими частотами f1, f2 на основе спектра ДПФ с учётом значения шага дискретности по частоте f может

быть сформулировано следующим образом. Если для частот составляющих в сигнале выполняется неравенство

129

f1 f2		(5 10) f ,

то составляющие не разрешимы на основе ДПФ. Если для частот составляющих в сигнале выполняется противоположное неравенство

f1 f2		(5 10) f ,

то составляющие разрешимы на основе ДПФ.

4.3. Функция спектральной плотности мощности сигналов

4.3.1. Теорема Парсеваля

Существуют два подхода, которые обычно применяются при исследовании свойств и характеристик сигналов. Первый подход базируется на обычных представлених во временной области, при которых сигналы у(t) рассматриваются как функции времени для

t . Второй подход связан с представлениями в частотной области, при которых сигналы или образы сигналов в виде преобразований Фурье C( j ),рассматриваются как функции частоты для

. Указанные подходы, являющиеся равноправными и двойственными, базируются на возможности реализации прямого и обратного преобразований Фурье, взаимнооднозначно связывающих временные и частотные представления сигналов. Теорема Парсеваля позволяет устанавливать величину полной энергии комплексных сигналов с помощью интегрирования либо во временной, либо в частотной областях.

Основываясь на разд. 2.2, обратимся к выражению для вычисления энергии E комплексного сигнала у(t) во временной области в

виде интеграла

Е y* (t) y(t)dt.	(4.3.1)

Используем обратное и комплексно-сопряжённое обратное преобра-

зования Фурье, сформируем выражения для сигналов y(t)		и y* (t) :
y(t) C( j )e j t d ,	y* (t) C* ( j )e j t d .	(4.3.2)

Подставим выражения (4.3.2) в интеграл (4.3.1) и переставим порядки интегрирования

130

E C(

E C(

		C* ( j )e j 1t d
j )e j t d					dt,	(4.3.3)
			1	1
j )d C( j 1)d 1			e j( 1)t dt.

Последний интеграл будет представлять собой -функцию из разд. 2.5.3

e j( 1)t d 2 ( 1).

Нетрудно видеть, что справедливо равенство, из которого величина полной энергии сигнала может быть вычислена на основе интегрирования в частотной области:

E	C( j )d C* ( j 1)d 12 ( 1) 2 С*( j )С( j )d .,		(4.3.4)
	Е	y* (t) y(t)dt 2 С* ( j )С( j )d .	(4.3.5)

Равенство (4.3.5) представляет собой формулировку теоремы Парсеваля и позволяет вычислять полную энергию сигнала как во временной, так и в частотной областях.

Прямое и обратное ДПФ может служить дискретным аналогом прямого и обратного непрерывного преобразования Фурье. Разберём вывод дискретного аналога теоремы Парсеваля.

Запишем обратное и сопряжённое обратное ДПФ для дискретных значений сигнала y(i), i 0, 1,..., N 1:

N 1	N 1
y(i) c(k)W ki ,	y* (i) c* (k)W ki .
k 0	k 0

Образуем произведения y*(i) y(i), просуммируем их по i, изменим порядок суммирования и получим

N 1	N 1 N 1		N 1
E y* (i) y(i)		c* (k)W ki c(k)W si
i 0	i 0	k 0	s 0

N 1	N 1	N 1	N 1
c* (k) c(s) W (s k )i N c* (k)c(k).				(4.3.6)
k 0	s 0	i 0	k 0
			131

На основе (4.3.6) сформируем выражение, которое является дискретным аналогом теоремы Парсеваля:

N 1	N 1
E y* (i) y(i)	N c* (k)c(k).	(4.3.7)
i 0	k 0

4.3.2. Определение функции спектральной плотности мощности сигналов

Определение функции спектральной плотности мощности (СПМ) сигналов связано с аналогией из электротехники – вычислении мощности, выделяемой на активном сопротивлении

(см. разд. 2.2).

Применим теорему Парсеваля (4.3.5) для нахождения величины энергии сигнала y(t), приходящейся на узкий интервал частот

( , d ) :

E( y, , d ) 2 C*y ( j )Cy ( j )d .

Для функции спектральной плотности мощности для стационарного эргодического сигнала Pyy ( ) в непрерывном случае сформи-

руем отношение части мощности сигнала в частотном диапазоне ( , d ) к величине d . Для этого рассмотрим прямое и ком-

плексно-сопряжённое прямое	преобразование Фурье для сигнала
y(t) на интервале времени T0		/ 2 t T0 / 2,		которые представля-
ются интегралами
		T /2
Сy ( j ,T0 )	1	0	y(t)e j t dt,
	2 T0		/2	(4.3.8)
		T /2
С*y ( j ,T0 )	1	0	y* (t)e j t dt.
	2 T0 /2
Энергия сигнала y(t) длительностью T0 в				частотном диапазоне

( , d ) может быть найдена на основе интегралов (4.3.8)

E( у, , d , T0 ) 2 C*y ( j , T0 )Cy ( j , T0 )d .

Функция СПМ Pyy ( ) для рассматриваемого стационарного эрго-

дического сигнала запишется в виде предела, в предположении, что этот предел существует:

132

	1	E( y, , d ,T )		2	C* ( j ,T )C			( j ,T )d
							y
	0				y	0		0
Pyy ( ) lim	T0		lim	T0					,
		d				d
T0			T0

P ( )	lim	2	C* ( j ,T )C		( j ,T ).	(4.3.9)
yy			y	0 y	0
	T0 Т0

Функция Pyy ( ) в общем случае определена во всём частотном диапазоне и является положительной Pyy ( ) 0.

Рассмотрим обобщение определения функции СПМ сигналов (4.3.9) для дискретного случая. Пусть задаётся набор дискретных значений сигнала y(i) y(Ti), i 0, 1,..., N 1, T – интервал дис-

кретизации. Интегралы Фурье из (4.3.8) могут быть заменены дискретными суммами, которые являются фактически оценками ука-

занных интегралов

для

заданной

частоты

k 2 k/(NT ),

k 0, 1,..., N 1 и и с учётом t Ti,

T0 TN :

1

N 1

j

2

kTi

1

Cy ( j k , TN )

T y(i)e

NT

TNcу (k),

2

i 0

2

C

* ( j , TN )

1

TNc*

(k). .

y

k

2

у

Нетрудно видеть, что оценки интегралов Фурье сформированы в виде ДПФ. Поэтому Pyy ( k ) – оценка функции СПМ дискретизо-

ванного сигнала для фиксированных частот k – может быть вычислена через коэффициенты ДПФ:

P ( )

2

C

*

( j ,TN )C

( j ,TN )

2

1

TNc* (k)

1

TNc(k),

y

y

yy k

TN

k

k

TN

2

2

P ( ) P c*(k)c(k),		k 0, 1,..., N 1,	P	TN	.	(4.3.10)
yy k	0		0	2
4.3.3. Функции временных окон
Погрешности	предложенной оценки (4.3.10) функции СПМ

Pyy ( k ) стационарного эргодического сигнала обусловливаются, в

основном, двумя факторами: заменой непрерывного сигнала на дискретный и конечностью интервала наблюдения. Точность оце-

133

нивания функции СПМ будет повышаться при уменьшении интервала дискретизации и увеличении длительности времени наблюдения.

Проанализируем возможность повышения точности оценивания функции СПМ для фрагмента сигнала, определённого на некотором конечном интервале времени. Рассмотрим погрешность, которая вносится конечностью интервала интегрирования при вычислении преобразований Фурье. Для сигнала y(t) запишем преобра-

зование Фурье на бесконечном и конечном симметричном временном интервале Т0 /2 t T0 /2 :

		1						1	T0 /2
	C( j )				y(t)e j t dt,	C ( j ,T )				y(t)e j t dt.
		2						2
						0	0
									T /2
									0
	Очевидно,	что			С( j ) С0 ( j , T0 )		и	С( j , T0 ) С( j )

С0 ( j , T0 ) – погрешность преобразования Фурье сигнала y(t),

вызванная					конечным интервалом интегрирования;			С2 (T )
								0
				С( j ,	T0 )		– мера погрешности. Преобразование Фурье на ко-

нечном интервале может замениться вычислением интеграла на бесконечном интервале, если ввести функцию прямоугольного

временного окна w0 (t, T0 ) 1				для Т0 /2 t T0 /2 и			w0 (t, T0 ) 0
для t T0 /2,	t T0 /2:
	С ( j , T )		1	w (t, T ) y(t) e j t dt.
	0	0	2		0	0

При стремлении величины временного интервала интегрирования T0 к бесконечности имеет место очевидный предел

lim С2 (Т0 ) 0.

T0

Согласно сделанным ранее рассмотрениям в разд. 2.5.3, преобразование Фурье от произведений функций вычисляется как интегральная свёртка преобразований Фурье сомножителей:

C0 ( j , T0 ) W0 ( j( 1), T0 )С( j 1)d 1,	(4.3.11)

где W0 ( j , T0 ) – преобразование Фурье функции прямоугольного временного окна w0 (t, T0 ). Приведём выражение преобразования

134

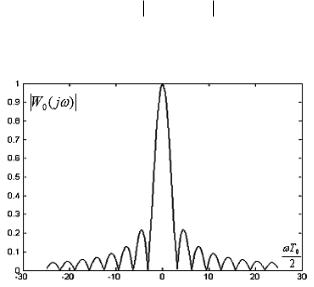
Фурье, которое в силу чётности w0 (t, T0 ) является действительной функцией

					T		sin		T0
									2
		W ( j , T )			0						.	(4.3.12)
					2
0			0					T0
									2
График модуля		W0 ( j , T0 )		для частного значения T0 /2 1 изо-

бражён на рис. 4.3.1. Функция W0 ( j , T0 ) состоит из главного лепестка, ширина которого определяется из соотношения T0 /2 , и системы медленно спадающих по амплитуде боковых лепестков.

Рис. 4.3.1. Модуль преобразования Фурье функции прямоугольного окна

При увеличении Т0 для прямоугольного окна его преобразование Фурье W0 ( j , T0 ) вида (4.3.12) стремится к -функции; преобразование Фурье С0 ( j , T0 ), в соответствии с формулой интегральной свёртки (4.3.11), стремится к С( j )

lim W0 ( j , T0 ) ( ),	lim С0 ( j , T0 ) С( j ).
T0	T0

Возможность снижения погрешности оценивания функции СПМ, возникающей из-за конечности временного интервала, может реализовываться на основе выбора подходящей функции вре-

менного окна w(t, T0 ) w0 (t, T0 ),	w(t, T0 ) 0 вне интервала
135

Т0 /2 t T0 /2. Умножение сигнала y(t) на функцию временного

окна w(t, T0 ) на интервале Т0 /2 t T0 /2,			y(t, T0 ) y(t)w(t, T0 )
описывается свёрткой в частотной области
C		( j ,T0 ) W ( j( 1),T0 )С( j 1)d 1.		(4.3.13)

Пусть функция временного окна w(t, T0 ) будет устроена таким образом, что её преобразование Фурье W ( j , T0 ) оказывается близким к -функции; W ( j , T0 ) должна будет иметь высокий и

узкий главный лепесток и систему малых боковых лепестков. Тогда имеются основания полагать, что в результате интегрирования

свёртки (4.3.13) преобразование Фурье C( j ) будет близко к C( j ). Последнее соответствует реализации приближённого равенства C( j ) C( j ), что эквивалентно снижению погрешности

при оценивании функции СПМ.

Перейдём к дискретным значениям сигнала y(i), 0 i , и функции временного окна w(i), определённой на конечном интер-

вале наблюдения i 0, 1,...,		N. После умножения наблюдений на
функцию	временного окна	получим последовательность y(i)
w(i) y(i),	i 0, 1,..., N..

Вычислим z-преобразование для последовательности y(i), ко-

торое может быть найдено на основе z-преобразований последовательностей y(i) и w(i) :

	N
Y (z) y(i)z i ,	W (z) w(i)z i ,	Z{y(i)} Y		(z).
i 0	i 0

Воспользуемся материалами разд. 2.6 и формулой (2.6.3), сделаем подстановку z e j T и запишем выражение для частотной функции Y (e j T ) на основе свёртки частотных функций окна W (e j T ) и сигнала Y (e j T ) :

				T	2 /T
			(e j T )			W (e j 1T )Y (e j( 1)T )d 1.
	Y
				2
					0

Очевидно, для того, чтобы частотная функция Y (e j T ) была близка к частотной функции Y (e j T ), необходимо, чтобы частотная

136