gos / Гетманов2

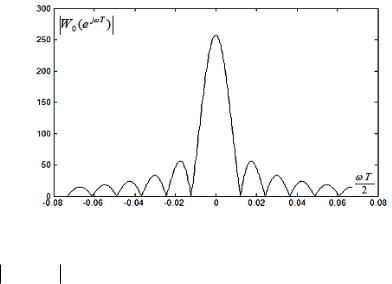
функция окна W (e j T ) была близка к -функции – имела бы высо-

кий главный лепесток в узком частотном диапазоне и незначительные боковые лепестки.

Рассмотрим некоторые варианты оконных функций. Примем для удобств выкладок временной интервал симметричным, положим N чётным и определим окно в точках N /2 i N /2 (в N + 1

точках).

Функция прямоугольного временного окна w0 (i) является ба-

зисной для настоящего рассмотрения и представляется соотношениями

w0 (i) 1 для N /2 i N /2 , w0 (i) 0 для i N /2, i N /2 .

Вычислим в соответствии с (2.6.3) частотную функцию для прямоугольного окна

		N /2		e j TN /2 e j TN /2e j T
W0 (e j T )		e j Ti
						1 e j T
		i N /2
	e j T ( N 1)/2		e j T ( N 1)/2			sin( T (N 1)/2)	.	(4.3.14)
	e j T /2		e j T /2			sin( T /2)

В силу чётности w0 (i) функция W0 (e j T ) является действительной.

Рис. 4.3.2. Модуль частотной функции прямоугольного окна

На рис. 4.3.2 изображён график модуля частотной функции W0 (e j T ) в зависимости от переменой Т /2, для примера взято

137

значение N 256. Частотная функция W0 (e j T ) является аналогом преобразования Фурье W0 ( j , T0 ).

Функции временных окон Хэннинга wH (i) и Хэмминга wHm (i) отличаются параметрами и описываются формулой

wH (i) (1 )cos(2 i / N) для N / 2 i N / 2,

wN (i) 0 для i N / 2, i N / 2, (4.3.15)

для окна Хэннинга выбирается значение 0,5 , для окна Хэмминга – 0,54 .

Вычисления частотных функций окон Хэннинга и Хэмминга производятся на основе частотных функций прямоугольного окна, сдвинутых вправо и влево на :

W (e j T ) sin( T (N 1) / 2)

H

sin( T / 2)

1 sin( T (N 1) / 2

(N 1) / N )

(4.3.16)

2

sin( T / 2

/ N )

1 sin( T (N 1) / 2

(N 1) / N )

.

2

sin( T / 2

/ N )

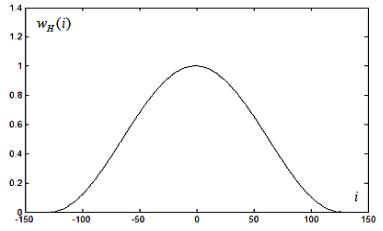
На рис. 4.3.3а, 4.3.3б изображены функция временного окна Хэннинга wH (i) для N 256 и модуль её частотной функции в зависимости от переменой Т /2.

Рис. 4.3.3а. Функция временного окна Хэннинга

138

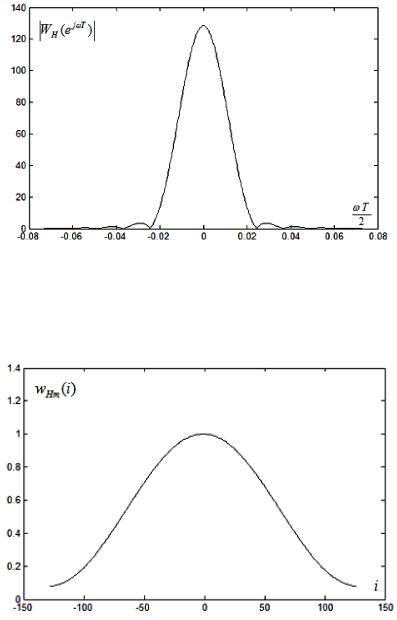
Рис. 4.3.3б. Модуль частотной функции окна Хэннинга

Рис. 4.3.4а, 4.3.4б содержат изображения функции временного окна Хэмминга wHm (i) для N 256 и модуля её частотной функции.

Рис. 4.3.4а. Функция временного окна Хэмминга

139

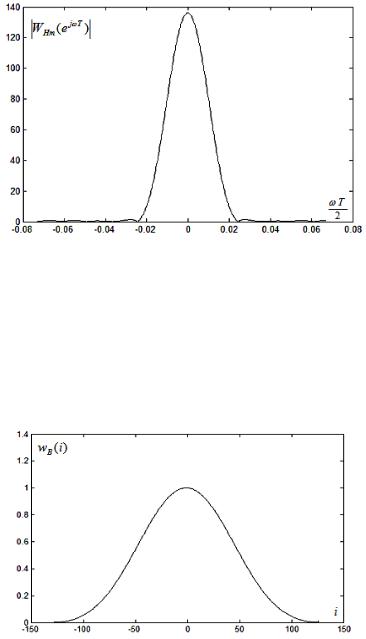
Рис. 4.3.4б. Модуль частотной функции окна Хэмминга

Функция временного окна Блэкмана wB (i) описывается весовой функцией

wB (i) 0, 42 0,5сos2 i / Ni 0,08cos 4 i / N
для	N /2 i N /2 ,	(4.3.17)
wB (i) 0	для i N /2, i N /2 .

На рис. 4.3.5а, 4.3.5б изображены функция временного окна Блэкмана wB (i) для N 256,и модуль частотной функции окна Блэкмана.

Рис. 4.3.5а. Функция временного окна Блэкмана

140

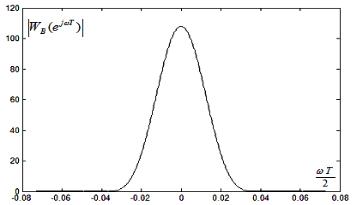
Рис. 4.3.5б. Модуль частотной функции окна Блэкмана

Функции временных окон wH (i), wHm (i) и wB (i) при визуаль-

ном анализе не очень сильно отличаются друг от друга. Однако различия в кривизне окон во временной области приводят к их существенным отличиям в частотной области – в размерах главного и боковых лепестков модулей частотных функций. Очевидно, что требования снижения ширины главного лепестка и амплитуд боковых лепестков являются противоречивыми.

Наглядное представление о частотных характеристиках функций временных окон могут дать графики модулей частотных функций в логарифмическом масштабе. С их помощью можно оценить ширину главных лепестков В Т и соотношение амплитуд главных

и первого бокового лепестков – коэффициент пульсации k р . На

рис. 4.3.6а для

прямоугольного

окна

изображён график

L

W (e j T )

20log

W (e j T )

,

на рис. 4.3.6б–4.3.6г, соответст-

0

10

0

венно, – графики

L

W (e j T )

,

L

W

(e j T )

и L

W (e j T )

.

H

Hm

B

Сравнительные характеристики функций временных окон для N 256, позволяющие судить об их эффективности при решении задачи повышения точности оценивания функций СПМ, помещены в табл. 4.3.1.

141

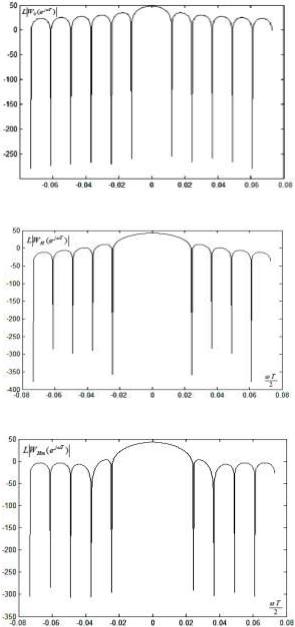
Рис. 4.3.6а. Модуль частотной функции прямоугольного окна в логарифмическом масштабе

Рис. 4.3.6б. Модуль частотной функции окна Хэннинга в логарифмическом масштабе

Рис. 4.3.6в. Модуль частотной функции окна Хэмминга в логарифмическом масштабе

142

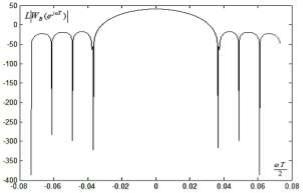
Рис. 4.3.6г. Модуль частотной функции окна Блэкмана в логарифмическом масштабе

			Таблица 4.3.1
	Тип окна	Ширина главного	Коэффициент
		лепестка В Т	пульсаций K р , %
	Прямоугольное окно	2 / N	21,7
	Окно Хэннинга	4 / N	2,64
	Окно Хэмминга	4 / N	1,23
	Окно Блэкмана	6 / N	0,112

4.3.4. Технологические этапы оценивания функции СПМ сигналов

Теперь опишем последовательность технологических этапов получения оценок функции СПМ для стационарных эргодических сигналов, наблюдаемых на большом интервале времени 0 t t f .

Будем полагать, что обрабатываемые сигналы y(t) задаются в не-

прерывной форме, например в виде записей на аналоговом магнитофоне.

Этап 1. Выбор частоты дискретизации. Пусть – верхнее значение частоты полосы сигнала. Чаще всего величина должна быть известной из априорных сведений о сигнале; полоса может регулироваться с помощью противомаскировочного фильтра. Согласно теореме Котельникова, частоту дискретизации d следует

выбирать, исходя из неравенства d 2 ( fd d /2 , Гц; T 1/ fd ). На практике обычно принимают частоту дискретизации

143

равной d (4 10) . Если в обрабатываемом сигнале доминирует

синусоидальная составляющая с частотой , то на период синусоиды T0 2 / должно приходиться (4 10) точек дискретизации. Общее число дискретизванных значений сигнала равняется вели-

чине N f	t f /T. Объём памяти ЭВМ (ДЗУ),	который займут вве-
дённые дискретизованные сигналы, в случае, если на одно			дис-
кретное	значение сигнала отводится	4 байта, составит

VДЗУ 4N f /1024 Кбайт. . При вводе дискретных данных в ЭВМ следует учитывать ограничение памяти ДЗУ ЭВМ VДЗУ – должно выполняться неравенство VДЗУ VДЗУ .

Этап 2. Выбор параметров локальных интервалов. Если N –

выбранное число точек на локальном интервале, m – число локальных интервалов, то должно выполняться условие Nm N f . Необ-

ходимо выбор параметров локальных интервалов осуществлять таким образом, чтобы числа N, m были целыми. Длина локального временного интервала NT подбирается, исходя из обеспечения требуемой разрешающей способности ДПФ f (см. разд. 4.2.3). Для этой цели должна быть определена минимальная разность частот двух соседних частотных составляющих f1 f2 в обрабатывае-

мом многочастотном сигнале. Величины f и f1 f2 для обеспе-

чения разрешения должны быть связаны неравенством, предложенным в разд. 4.2.3:

f1 f2 (5 10) f .

Для улучшения разрешения, естественно, следует назначать длинные локальные интервалы. Однако при обеспечении хорошего усреднения результатов цифровой обработки требуется увеличивать m – реализовывать большое количество локальных интервалов и тем самым уменьшать длины локальных интервалов. Требования удовлетворительного усреднения и хорошей разрешающей способности являются противоречивыми. Выбор параметров N, m

связан с принятием компромисса.

Этап 3. Умножение сигналов на локальных интервалах на функцию временного окна. Пусть для дискретизованного сигнала y(s), s 0, 1,..., N f 1, исходный большой интервал времени раз-

бивается на m локальных интервалов по N точек. Дискретизован-

144

ный сигнал на j-м локальном интервале имеет вид y(i N( j 1)), j 1,..., m, i 0, 1,..., N 1. Для каждого локального интервала

осуществляется умножение части дискретизованного сигнала на N- точечное временное окно w(i)

y(i N( j 1)) y(i N( j 1))w(i), j 1,..., m, i 0, 1,..., N 1.

Этап 4. Вычисление локальных ДПФ и локальных оценок функции СПМ. Нахождение локальных коэффициентов ДПФ производится в соответствии с формулой ДПФ

		1	N 1
	с j (k)		y(i N ( j 1))W ki ,	k 0, 1,..., N 1,	j 1,..., m.
		N i 0

Локальные оценки функции СПМ находятся с использованием локальных коэффициентов ДПФ

P	(k) P c* (k)c	j	(k),	k 0, 1,..., N 1,	j 1,..., m.
yy, j	0 j

Этап 5. Вычисление оценок функции СПМ. Оценка функции СПМ для стационарного эргодического сигнала вычисляется на

основе усреднения оценок Pyy, j (k) по множеству локальных интервалов

1 m

Pyy (k) m Pyy, j (k), k 0, 1,..., N 1. .

j 1

Усреднение обеспечивает снижение шумовых порешностей в оценке функций СПМ сигналов.

На основе предложенной последовательности технологических этапов оценивания функций СПМ достаточно эффективно решаются многие задачи оценивания параметров сигналов, которые иногда не могут быть успешно решены другими методами. Возникающие при этом погрешности в оценках в ряде случаев могут компенсироваться достигаемым большим быстродействием и простотой вычислительных процедур.

4.4.Функция взаимной cпектральной плотности мощности сигналов

4.4.1.Определение функции взаимной cпектральной плотности мощности сигналов

Определение функции взаимной спектральной плотности мощности (ВСПМ) сигналов вытекает из задачи электротехники – вычис-

145

лении выделяемой мощности на реактивном сопротивлении. В формировании функции ВСПМ участвуют сигналы x(t), y(t); функция

ВСПМ является обобщением функции СПМ на случай двух сигналов.

Запишем, опираясь на естественное обобщение теоремы Парсеваля (4.3.5), выражение для величины взаимной энергии сигналов x(t), y(t), приходящейся на интервал частот ( , d )

E(x, y, , d ) 2 C*( j )C		( j )d .	(4.4.1)
x	y

Для функции ВСПМ Pxy ( ) стационарных эргодических сигналов в

непрерывном случае сформируем отношение части взаимной мощности сигналов в частотном диапазоне ( , d ) к величине d .

Для этого рассмотрим комплексно-сопряжённое прямое и обычное прямое преобразования Фурье для сигналов x(t), y(t) на конечном

интервале времени T0 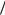2 t T0 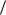2, которые представляются интегралами

			T /2
Сx* ( j , T0 )	1		0	x* (t)e j t dt,
	2 T /2
		0		(4.4.2)
			T /2
Сy ( j , T0 )	1		0	y(t)e j t dt.
	2 T /2
		0
Взаимная энергия сигналов	x(t), y(t) для интервала T0 /2 t

T0 /2 в частотном диапазоне ( , d ) может быть найдена на основе интегралов (4.4.2) с использованием выражения (4.4.1)

E(x, у, , d , T0 ) 2 Cx*( j , T0 )Cy ( j , T0 )d .

Функция ВСПМ Pxy ( ) для указанных сигналов, так же как и функция СПМ Pуy ( ) для разд. 4.3, запишется в виде предела, в предположении, что предел существует

	1	E(x, y, , d , T )		2	C* ( j , T )C			( j , T )d
							y
	0				x	0		0
Pxy ( ) lim	T0		lim	T0					,
		d				d
T0			T0

P ( )	lim	2	C* ( j , T )C		( j , T ).	(4.4.3)
xy			x	0 y	0
	T0 Т0
		146