gos / Гетманов2

Функция ВСПМ сигналов, определённая в общем случае во всём частотном диапазоне , в отличие от функции СПМ является комплексной, что следует из определения (4.4.3) и пред-

ставляется соотношением P	( ) P	( ) jP	( ),	где P	( ),
xy	1xy	2xy		1xy

P2xy ( ) – действительная и мнимая составляющие функции ВСПМ. Возможно представление функции ВСПМ в показательной форме

P ( )

P ( )

e j xy ( ) ,

xy

xy

– функция модуля; xy ( ) – функция фазового угла

где

Pxy ( )

функции ВСПМ сигналов;

P ( )

(P2

( ) P2 ( ))1/2 ,

xy

( )

xy

1xy

2xy

arctg(P

( ) / P

( )). Из определения для функции ВСПМ сиг-

2xy

1xy

налов вытекает, что P ( ) P*

( ).

yx

xy

Рассмотрим обобщение определения функции ВСПМ сигналов (4.4.3) для дискретного случая и конечного интервала времени. Пусть задаётся набор дискретных значений сигналов x(i) x(Ti),

y(i) y(Ti), i 0, 1,..., N 1, T – интервал дискретизации. Интегра-

лы Фурье из (4.4.2) заменяются дискретными суммами, которые можно принять в качестве оценок указанных интегралов для задан-

ной частоты k 2 k /(NT ),

k 0, 1,..., N 1

и с учётом t Ti,

T0 TN:

1

N 1

j

2

1

T y(i)e

NT

kTi

Cy ( j k , TN )

2

TNcу (k),

i 0

2

C * ( j , TN )

1

TNc*

(k).

(4.4.4)

х

k

2

x

Нетрудно видеть, что оценки интегралов Фурье (4.4.4) сформированы в форме ДПФ. Поэтому Pxy ( k ) – оценка функции ВСПМ

дискретизованного сигнала для фиксированных частот k может

быть выражена через коэффициенты ДПФ:

P ( )

2

C *

( j , TN )C

( j , TN )

y

xy k

TN

x

k

k

2

1

TNc*x (k)

1

TNcy (k) ,

TN 2

2

147

P ( ) P c* (k)c			(k),	k 0, 1,..., N 1,	P	TN	.	(4.4.5)
		y
xy k	0 x				0	2

Действительные и мнимые компоненты оценки функции ВСПМ (4.4.5) вычислим через действительные и мнимые коэффициенты ДПФ:

Pxy (k) P0 (c1x (k) jc2x (k))(c1y (k) jc2 y (k)),

P	(k) P (c	(k)c	(k) c	(k)c	(k)),
1xy	0 1x	1y	2x	2 y

P2xy (k) P0 (c1x (k)c2 y (k) c2x (k)c1y (k)).

Если дискретизованные сигналы x(i), y(i) являются комплекс-

ными одночастотными синусоидами, которые отличаются начальными фазами, то, очевидно, функция модуля функции ВСПМ для этой пары сигналов ведёт себя почти аналогично функции модуля ДПФ комплексной синусоиды.

Когда для стационарных эргодических сигналов оценивание функции ВСПМ осуществляется на большом временном интервале, то указанная оценка может находиться с помощью усреднения. Для этой цели на большом временном интервале формируются локальные интервалы, на которых вычисляются локальные коэффициенты ДПФ исследуемой пары сигналов, с учётом умножения на функции временных окон. Далее находятся локальные оценки функции ВСПМ, которые затем усредняются.

Пусть реализованы дискретизованные сигналы x(t), y(t), s 0, 1,..., N f 1; m – число локальных интервалов; N – число точек на локальном интервале, Nm N f . Сигналы, соответствующие j-му локальному интервалу, имеют вид x(i N( j 1)) y(i N( j 1)), j 1,..., m, i 0, 1,..., N 1. Для каждого локально-

го интервала осуществляется умножение части дискретизованных сигналов на выбранное N – точечное временное окно w(i) :

x(i N( j 1)) x(i N( j 1))w(i), y(i N( j 1)) y(i N( j 1))w(i),

j 1,..., m, i 0, 1,..., N 1,

и нахождение локальных коэффициентов ДПФ

148

	1	N 1			1		N 1
сx, j (k)		x (i N ( j 1))W ki ,	сy, j (k)				y(i N ( j 1))W ki ,
	N i 0				N i 0
		k 0, 1,..., N 1,		j 1,...,		m.

Оценивание комплексной функции ВСПМ сигналов производится отдельно для действительной и мнимой компонент на основе усреднения

1

m

Pxy, j (k) P0c*x, j (k)cy, j (k),

j 1,..., m,

Pxy (k)

Pxy, j (k),

m j 1

1

m

1

m

P

(k)

P

(k), P

(k)

P

(k),

(4.4.6)

1xy

1xy, j

2xy

2xy, j

m j 1

m j 1

k 0,

1,..., N 1. .

Вычисление оценок функций модуля и функций фазового угла производится на основе (4.4.6) и представляется формулами

P		(k)	(P	(k)2	P	(k)2 )1/2		,
	xy		1xy		1xy
	xy	(k) arctg(P			(k) / P		(k)),	(4.4.7)
				2xy		1xy

k0, 1,..., N 1.

4.4.2.Применение функции ВСПМ в задачах оценивания разностей фаз для систем многочастотных сигналов

Применение функции ВСПМ позволяет решать задачи оценивания разностей фаз для систем сложных многочастотных сигналов.

Прежде всего, отметим, что для двух синусоидальных сигналов x(t), y(t) с постоянными во времени амплитудами и одинаковыми

частотами, которые описываются системой

x(t) A1 cos( t 1),	y(t) A2 cos( t 2 ),	(4.4.8)
разность фаз xy определяется	как разность фазовых	функций

1(t) t 1, 2 (t) t 2 , что в данном случае эквивалентно

разности начальных фаз

xy 1 2 .

В том случае, если сигналы x(t), y(t) являются многочастотными, состоящими из суммы синусоидальных составляющих с одинако-

149

выми частотами, то разности фаз xy,l , l 1,..., L определяются

отдельно для каждой пары составляющих с одинаковыми частотами

L		L
x(t) A1l cos( lt 1l ) ,		y(t) A2l cos( l t 2l ) ,
l 1		l 1
xy,l	1,l 2,l .		(4.4.9)

Определение разностей фаз для многочастотных сигналов (4.4.6) является естественным обобщением определения разностей фаз для одночастотного случая (4.4.8).

Возможно определение функций разностей фаз (4.4.8) и (4.4.9) на случай полосовых сигналов

x(t) Е1(t)cos 1(t), y(t) Е2 (t)cos 2 (t), (4.4.10)

где E1(t), E2 (t) – медленно меняющиеся амплитудные функции;1(t), 2 (t) – фазовые функции. Для полосовых сигналов в общем случае разность фаз меняется во времени xy (t) 1(t) 2 (t). В

ряде случаев разность фаз для сигналов (4.4.10) на некотором интервале времени 0 t t f может изменяться незначительно и при-

ниматься в виде константы xy (t) xy . Соотношения

L		L
x(t) Е1l (t)cos 1l (t),	y(t) Е2l (t)cos 2l (t),
l 1		l 1
xy,l (t) 1,l (t) 2,l (t),		l 1,..., L,	(4.4.11)

служат определением разностей фаз для сигналов, являющихся суммой полосовых сигналов.

Представим некоторые модельные варианты систем сигналов, для которых здесь рассматривается задача оценивания разностей фаз.

Модель системы сигналов x(t), y(t) в простейшем случае описывается соотношениями

x(t) A1 cos( t 1) w1(t), y(t) A2 cos( t 2 ) w2 (t), (4.4.12)

которые представляют собой аддитивную смесь монохроматических сигналов и широкополосных шумов w1(t), w2 (t) (белых шу-

мов). Оценивание разностей фаз xy для (4.4.12) производится на

150

основе цифровой обработки зашумлённых сигналов x(t), y(t) (4.4.12) на заданном интервале времени 0 t t f .

Модель системы сигналов x(t), y(t) для многочастотного случая описывается соотношениями

L
x(t) Е1l (t)cos 1l (t) w1(t) ,
l 1
L
y(t) E2l (t)cos 2l (t) w2 (t) .		(4.4.13)
l 1
Вычисление оценок разностей фаз xy,l ,	l 1,..., L,	для частот-

ных составляющих сигналов производится на основе цифровой обработки зашумлённых многочастотных сигналов x(t), y(t) (4.4.13)

на заданном интервале времени 0 t t f .
Перейдём к	дискретизованным сигналам	x(i) x(Ti),
y(i) y(Ti), которые	определены в N точках, i 0,	1,..., N 1. На-

метим подход к оцениванию разностей фаз колебательных сигналов с использованием оценок функций ВСПМ. Пусть заданы два синусоидальных комплексных дискретизованных сигнала

	x(i) A e j W qi ,	y(i) A W qi , i 0, 1,..., N 1,		(4.4.14)
	1	2
где A , A – постоянные амплитуды; W e j2 / N ;			T – интервал дис-
1	2
кретизации; f – частота сигналов; q f /(1/ NT )),			q q0	q, q0 –

целое, q 1. Очевидно, разность фаз между сигналами x(i), y(i) (4.4.14), по определению, xy .

Найдём оценку функции ВСПМ для сигналов (4.4.14). Вычислим коэффициенты ДПФ cx (k), cy (k) cигналов x(i), y(i), пусть

с(k) – коэффициенты ДПФ для W qi . Тогда очевидны соотношения, вытекающие из (4.4.14),

c	x	(k) A e j c(k),	c* (k) A e j 1c* (k),		c	y	(k) A c(k).
		1	x	1			2

На основе cx (k), cy (k) запишем выражения для оценки функции ВСПМ сигналов – оценки её модуля и фазового угла

P (k) P A e j c* (k)A c(k),					P (k)		P A A		c(k)		2	,			(k) .
xy	0 1	x	2		xy		0 1 2							xy
				151

Заметим, что в данном частном случае для комплексных синусоидальных сигналов фазовый угол функции ВСПМ не зависит от индекса k. Будем находить оценку искомой разности фаз xy из

оценки фазового угла ВСПМ в точке координаты максимума модуля функции ВСПМ. В данном случае эта координата равна k q0:

q	arg{max		P (k)		2	},		xy		xy	(q ) .
0	k		xy								0

Продолжим рассмотрение задачи оценивания разности фаз, когда два синусоидальных комплексных сигнала аддитивно смешаны с шумами:

x(i) A e j W qi w (i),		y(i) A W qi w (i),		i 0, 1,..., N 1, (4.4.15)
1	1	2	2

где w1(i), w2 (i) – шумовые комплексные последовательности независимых нормальных случайных чисел с нулевым математическим ожиданием и дисперсией 2 .

Коэффициенты ДПФ для синусоид x(i), y(i) (4.4.15) запишутся с учётом аддитивности шумов:

с	x	(k) A e j c(k) c (k),		с	x	(k) A e j c(k) c (k),
		1	w			1	w
			1				1

где	сw (k), cw (k)		– коэффициенты ДПФ для	w1(i), w2 (i), i 0,
	1	2
1,..., N 1.		Для точки k q0 и в её окрестности, соответствующей

расположению максимума модуля функции ВСПМ, должны выполняться неравенства, при условии малых 2 :

сw1 (q0 ) A1c(q0 ) , сw2 (q0 ) A2c(q0 ) .

Для оценки функции ВСПМ комплексных синусоидальных сигналов (4.4.15) оказываются справедливыми приближённые равенства с учётом малости шумов:

Р (q )		P A A		c(q )		2	,		xy		xy	(q ) .
xy 0		0 1 2		0								0

Алгоритм оценивания разностей фаз для системы синусоидальных сигналов в шумах на основе функций ВСПМ, таким образом, состоит из этапов: 1) вычисления оценки функции ВСПМ сигналов

Pxy (k),			k 0, 1,..., N 1 и её составляющих – функции модуля
	Pxy (k)		и функции фазового угла xy (k); 2) вычислении координа-

ты максимума функции модуля ВСПМ

152

q0 k ,	k arg{ max	Pxy (k)	};
	k 0,1,...,N 1

3) вычислении оценки разности фаз по функции фазового угла ВСПМ xy xy (q0 ). Для повышения точности оценивания раз-

ности фаз на больших временных интервалах применяется процедура усреднения. Предложенный алгоритм может быть обобщён на случай многочастотных сигналов.

Рассмотрим численный пример моделирования предложенного алгоритма оценивания разности фаз для системы зашумлённых

двухчастотных сигналов.
Смоделируем систему предлагаемых сигналов	x(i) x(Ti),
y(i) y(Ti), определённых в N f точках, i 0, 1,..., N f	1,
x(i) A11 cos(2 f1Ti 11) A12 cos(2 f2Ti 12 ) w1(i),
y(i) A211 cos(2 f1Ti 21)
A22 cos(2 f2Ti 22 ) w2 (i) .	(4.4.16)

Для (4.4.16) дискретные шумы w1(i), w2 (i) моделируются независимыми нормальными числами с нулевыми математическими ожи-

даниями и дисперсиями 2 , 2. Модельные сигналы (4.4.16) име-
			1	2
ют	следующие		исходные	параметры:		A11 1,0;		A12	2,0,
A21 4,5;		A22 5,5,	f1 10,0	Гц;	f2 18 Гц , 11		1,5;	12	4,0,
21	3,0;	22 1,0;	1 1,5;	2 1,5. Разности фаз, приведённые
к диапазону 2 для частотной составляющей с частотой									f1 , со-
ставляют величину 12,1 11 21 4,78,						для частоты		f2	– ве-
личину		12,2 12 22 3,0.			Интервал		дискретизации
T 0,01 c,		локальный интервал состоит из				N 512 точек,			число

локальных интервалов m 32.

На рис. 4.4.1а представлен график оценки модуля функции ВСПМ модельных сигналов (4.4.16) для диапазона 0 k N / 4 1. Положение максимумов может быть оценено на основе визуально-

го	анализа графика рис. 4.4.1а или, исходя из рассмотрений
разд. 4.2.1, q01 k1		f1NT 10 512 0,01 52.	Оценки разностей
фаз для составляющих сигнала c частотами			f1, f2 определяются
из	расчётов или	графика рис. 4.4.1б и принимают значения
		153

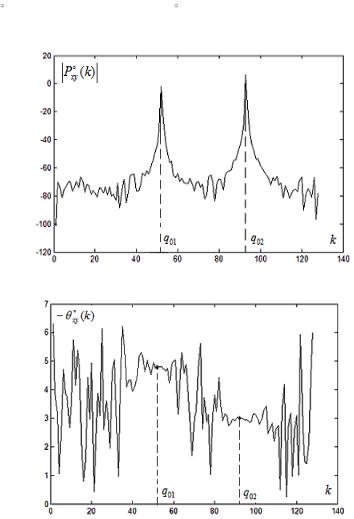
xy,1 xy (q01) 4,75,

xy,2 xy (q02 ) 3,02, удовлетвори-

тельно соответствующие исходным параметрам.

Рис.4.4.1а. Оценка модуля функции ВСПМ модельных сигналов (4.4.13)

Рис.4.4.1б. Оценка фазового угла функции ВСПМ модельных сигналов (4.4.13)

4.4.3.Применение функции ВСПМ для оценивания коэффициента когерентности колебательных сигналов

На основе ВСПМ вычисляется коэффициент когерентности xy , являющийся параметром, который служит мерой взаимосвязи двух

154

случайных сигналов x(t), y(t). Определим некоторые очевидные свойства, которыми может быть наделён вводимый коэффициент.

1. Коэффициент когерентности должен быть	ограниченным:
0 xy 1 (как один из вариантов определения).	Если xy 1, то
имеет место полная взаимосвязанность двух	сигналов; если

xy 0, то сигналы являются полностью несвязанными.

2. Очевидно, что для синусоидальных сигналов

y(t) A1 cos( t 1), x(t) A2 cos( t 2 )

коэффициент	когерентности	должен	удовлетворять равенству
xy 1. Для	синусоидальных	сигналов	аддитивно смешанных с

шумами

y(t) A1 cos( t 1) w1(t), x(t) A2 cos( t 2 ) w2 (t)

коэффициент когерентности должен быть меньше единицы xy 1.

Естественно, что при увеличении интенсивности шумов коэффициент когерентности уменьшается.

3. Если два случайных сигнала статистически независимы, например x(t) w1(t), y(t) w2 (t), – независимые белые шумы, то

должно выполняться соотношение xy 0.

4. Если два сигнала связаны некоторой линейной зависимостью, то, очевидно, xy 1.

Рассмотрим неравенство, позволяющее сделать обоснование для вводимого коэффициента когерентности:

сy (k) cx (k)e j yx (k ) с*y (k) c*x (k)e j yx (k ) 0.

Сделаем соответствующее перемножение модулей, получим в качестве слагаемых выражения для оценок функций СПМ и ВСПМ:

2Pyy (k) Pyx (k)e j yx (k ) Pxy (k)e j xy (k ) Pxx (k) 0.

Приведём соотношения, с помощью которых выведем основное неравенство, используемое для определения коэффициента когерентности:

P (k)

P (k)

e j yx

(k ) , P (k)

P (k)

e j yx (k ) ,

yx

yx

yx

yx

2P (k) 2

P (k)

P (k) 0.

yy

yx

xx

155

Последнее выражение можно рассматривать как квадратный полином от ; для обеспечения его положительности необходимо, чтобы его дискриминант был меньше нуля:

4

P (k)

2

4P (k)P (k) 0,

P (k)

2

P (k)P (k).

xy

xx

yy

xy

xx

yy

Полученное неравенство ложится в основу эмпирического определения функции коэффициента когерентности, для которого выполняется условие 0 xy 1:

xy (k)		Pxy (k)		2	.
	Pxx (k)Pyy (k)

С использованием оценок функций СПМ и ВСПМ сигналов записывается оценка функции коэффициента когерентности в дискретных частотных точках k :

	xy	( )		Pxy ( k )		2	,		2	k,	k 0, 1,..., N 1.
		k	Pxx ( k )Pyy ( k )				k		NT

Рассмотрим вычисление функции коэффициента когерентности

для комплексных синусоид без шумов. Положим x(i) A e j W qi ,

1

y(i) A W qi ,

c

(k) A e j c(k),

c

y

(k) A c(k).

Здесь c(k) – коэф-

2

x

1

2

фициенты ДПФ для W qi . Тогда

P (k) P c* (K)c

y

(k) P A A e j c* (k)c

(k),

xy

0 x

0 1

2

x

x

P (k)

2 P2

( A A )2

c(k)

2 ,

xy

0

1 2

P (k) P A2

c(k)

2 ,

P (k) P A2

c(k)

2 .

xx

0 1

yy

0

2

Видно, что для рассматриваемого примера имеет место равенствоxy 1. Для комплексных синусоид с малыми шумами

x(i) A e j W qi w (i),

y(i) A W qi w (i),

1

1

2

2

запишем выражения для коэффициентов ДПФ

c

x

(k) A e j c(k) c (k),

c

y

(k) A c(k) c (k).

1

w

2

w

1

2

Для k q0

(k q0 )

в предположении,

что

A1c(q0 )

cw (q0 )

,

1

A2c(q0 )

cw (q0 )

,

следует, что

xy (k q0 ) 1, для остальных

2

индексов xy (k q0 ) 0.

156