
- •Введение
- •1. Понятие оригинала
- •2. Изображение по лапласу
- •3. Изображения простейших элементарных функций
- •4.Свойства преобразования лапласа
- •2С) Теорема подобия
- •3C) Теорема затухания (Теорема смещения)
- •5C) Теорема опережения.
- •10С) Интегрирование изображений.
- •11С) Теорема умножения изображений (теорема Бореля)
- •12С) Умножение оригиналов.
- •5.Примеры нахождения изображений с помощью таблиц 1 и 2
- •6. Импульсные функции и их изображения
- •7.Формула обращения преобразования лапласа
- •1)Тождественные преобразования и применение таблиц 1 и 2.
- •2) Вычисление оригиналов с помощью вычетов.
- •8.Применение преобразования лапласа для решения уравнений и систем
- •8.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.2 Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.
- •8.3 Решение дифференциальных уравнений с переменными коэффициентами.
- •8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.5 Линейные дифференциальные уравнения с запаздывающим аргументом.
- •8.6 Интегральные уравнения типа «свертки».
- •8.7 Линейные интегро-дифференциальные уравнения.
- •9.Решение диференциальных уравнений в частных производных и задач математической физики
- •10. Применение операторных методов для анализа линейных систем
- •11. Дискретное преобразование лапласа. Z – преобразование лорана
- •1) Решетчатые функции.
- •2) Конечные разности решетчатых функций.
- •3) Суммирование решетчатых функций.
- •4) Определение дискретного преобразования Лапласа.
- •5) Формула обращения.
- •1С) Теорема линейности.
- •Библиографический список
- •Оглавление
УДК 51
Операционное исчисление и некоторые его приложения.
Математика-13: Учеб. пособ. / М.А. Евдокимов, Л.Г. Волкова; Самар. гос. техн. ун-т. Самара, 2007. 108 с.
Продолжает серию учебников по высшей математике, издаваемых на кафедре высшей математики и прикладной информатики. Предназначено для студентов, которые изучают раздел математики, посвященный операционному исчислению, и преподавателей, ведущих занятия по данной теме.
ISBN
Ил. 33. Библиогр.: 8 назв.
Печатается по решению редакционно-издательского совета
Самарского государственного технического университета
Рецензент д-р техн. наук Э.Я. Раппопорт
ISBN
Введение
В
![]() веке
многие математики (в том числе у нас в
России, например, М.Е.Ващенко - Захарченко
и А.В.Летников) занимались так называемым
символическим исчислением. В основе
этого исчисления лежало построение
математического анализа как системы
формальных операций над символом
веке
многие математики (в том числе у нас в
России, например, М.Е.Ващенко - Захарченко
и А.В.Летников) занимались так называемым
символическим исчислением. В основе
этого исчисления лежало построение
математического анализа как системы
формальных операций над символом
![]()
![]() (
(![]() -независимая
переменная).
-независимая
переменная).
Например,
![]() - ная производная функции
- ная производная функции
![]() представляется как результат действия
на
представляется как результат действия
на
![]() символа
символа
![]()
![]() ,
левая часть линейного дифференциального
уравнения с постоянными коэффициентами
,
левая часть линейного дифференциального
уравнения с постоянными коэффициентами
![]() -
как результат действия на
-
как результат действия на
![]() символа.
символа.
![]() .
.
Символическое
исчисление оказалось довольно удобным
для решения различных задач, связанных
с линейными дифференциальными уравнениями.
Его популяризации в
![]() веке
в сильной мере способствовал английский
инженер-электрик О.Хевисайд, который
успешно использовал символическое
исчисление в электротехнических
расчетах.
веке
в сильной мере способствовал английский
инженер-электрик О.Хевисайд, который
успешно использовал символическое
исчисление в электротехнических
расчетах.
Обоснование
символичного или, как стали называть,
операционного метода было дано лишь в
двадцатых годах двадцатого столетия
Бромвичем и Карсоном, связавшими этот
метод с известным из теории функций
комплексного переменного методом
интегральных преобразований, которым
с успехом пользовались Коши, Лаплас и
другие математики. При этом символ
(оператор)
![]() получил новое толкование, как комплексная
переменная
получил новое толкование, как комплексная
переменная
![]() ,
а вместе с ним новую трактовку получил
и сам операционный метод.
,
а вместе с ним новую трактовку получил
и сам операционный метод.
Операционный метод получил также иное строгое обоснование с помощью общей теории операторов, развитый в функциональном анализе, представленной в работах В.А.Диткина и А.П.Прудникова. В последнее время весьма оригинальную и простую трактовку операционного метода дал польский математик Ян Микусинский.
В данной работе излагаются основные положения операционного метода и особое внимание уделяется применению его для решения различных задач.
1. Понятие оригинала
Функцией-оригиналом
называется комплекснозначная функция
![]() действительного аргумента
действительного аргумента
![]() ,
которая удовлетворяет следующим
условиям:
,
которая удовлетворяет следующим
условиям:
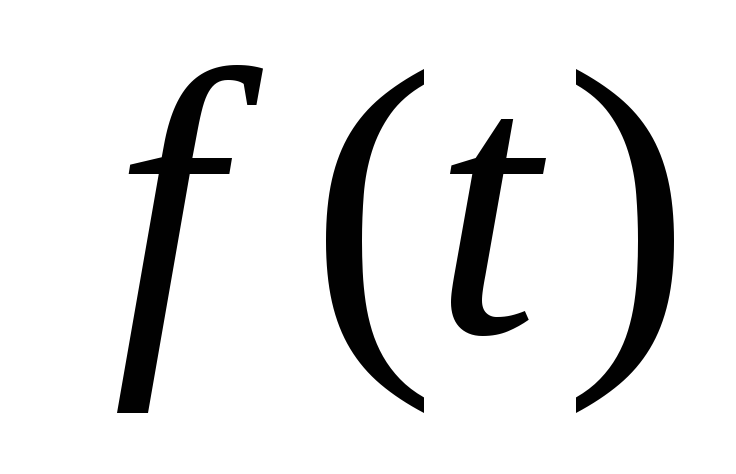 должна
быть кусочно-непрерывной при
должна
быть кусочно-непрерывной при
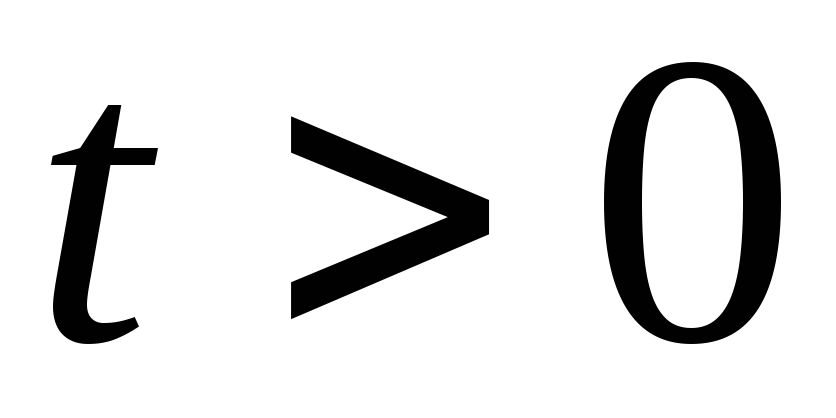 (то
есть должна быть непрерывной или иметь
конечное число точек разрыва
(то
есть должна быть непрерывной или иметь
конечное число точек разрыва
 рода).
рода).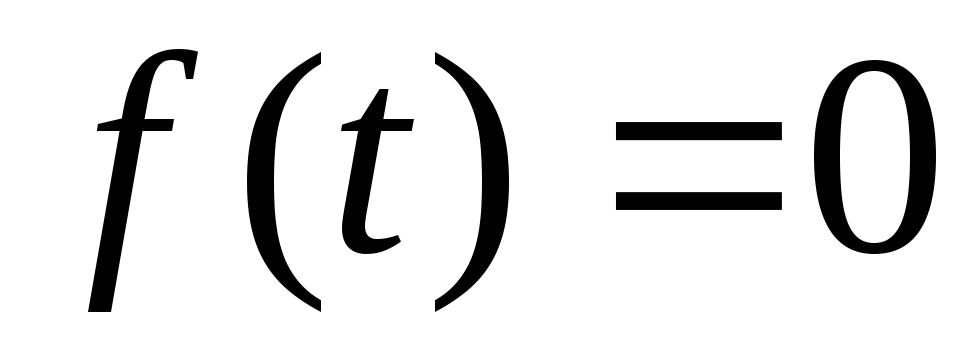 при
при
 .
(Это означает, что нас не интересует
предыстория процесса).
.
(Это означает, что нас не интересует
предыстория процесса).При возрастании
 модуль
модуль
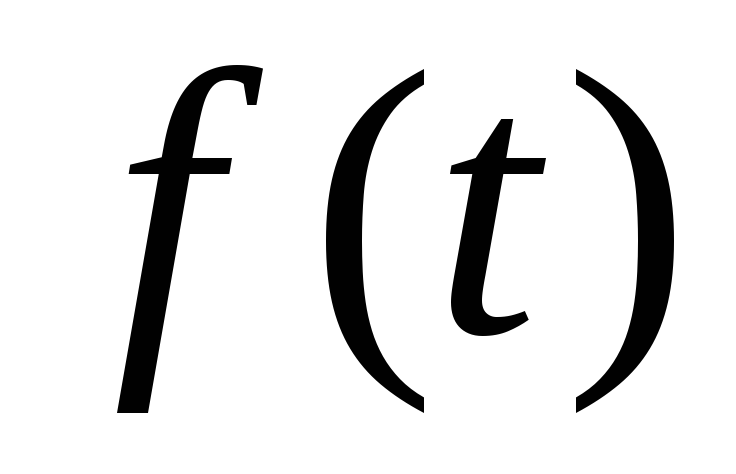 может возрастать, но не быстрее некоторой
показательной функции: т.е. существуют
такие постоянные
может возрастать, но не быстрее некоторой
показательной функции: т.е. существуют
такие постоянные
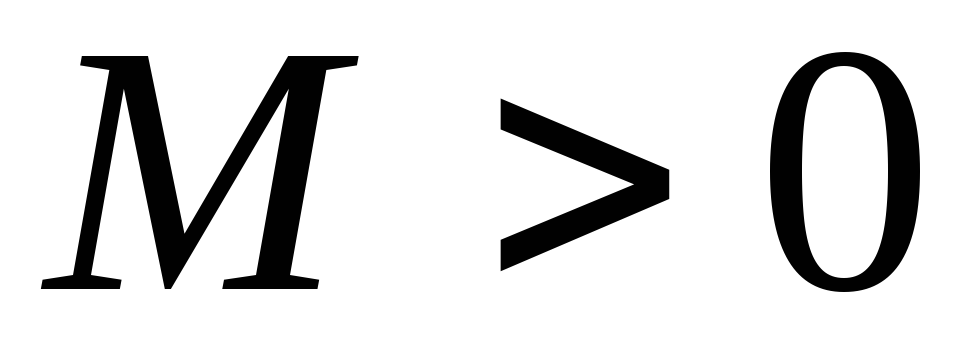 ,
,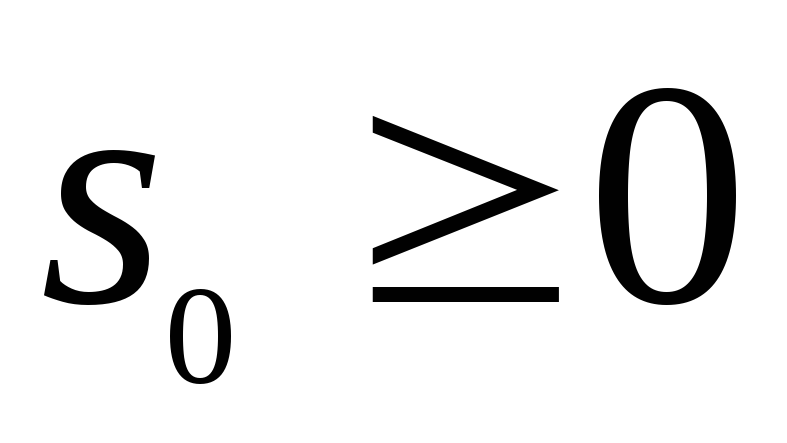 ,
что для всех
,
что для всех выполняется неравенство:
выполняется неравенство:
![]() .
.
Число
![]() называется
показателем роста
называется
показателем роста
![]() ,
для ограниченных оригиналов можно,
очевидно, принять
,
для ограниченных оригиналов можно,
очевидно, принять
![]() .
.
С
точки зрения физических приложений
условий 1) и 3) не нуждаются в пояснениях
– они, очевидно, выполняются для
большинства функций
![]() ,
описывающих физические процессы (
,
описывающих физические процессы (![]() интерпретируется как время). Условие
2), на первый взгляд, кажется искусственным,
однако, следует иметь в виду, что
операторный метод приспособлен к
задачам, приводящим к решению
дифференциальных уравнений с данными
начальными условиями. В таких задачах
вся информация о ходе процесса до момента
начала наблюдения, за которой, конечно,
можно принять момент
интерпретируется как время). Условие
2), на первый взгляд, кажется искусственным,
однако, следует иметь в виду, что
операторный метод приспособлен к
задачам, приводящим к решению
дифференциальных уравнений с данными
начальными условиями. В таких задачах
вся информация о ходе процесса до момента
начала наблюдения, за которой, конечно,
можно принять момент![]() ,
содержится в начальных условиях. Таким
образом, и условие 2) физически, вполне,
естественно.
,
содержится в начальных условиях. Таким
образом, и условие 2) физически, вполне,
естественно.
П
![]()
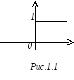
T

Очевидно,
умножение
![]() на
на![]() гасит эту функцию для
гасит эту функцию для
![]() и оставляет без изменения для
и оставляет без изменения для![]() ;
если функция
;
если функция
![]() удовлетворяет условиям 1) и 3) и не
удовлетворяет 2), то произведение
удовлетворяет условиям 1) и 3) и не
удовлетворяет 2), то произведение
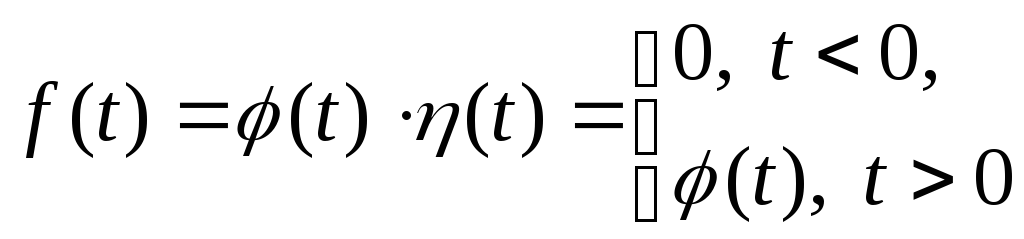
будет
удовлетворять условию 2), т.е. будет
оригиналом (например,
![]() (рис.1.2)).
(рис.1.2)).
f(t)=sin(t)


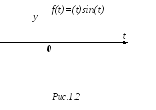

Для
простоты записи будем, как правило,
опускать множитель
![]() ,
условившись, раз и навсегда, что все
функции, которые мы будем рассматривать,
равны нулю для отрицательных
,
условившись, раз и навсегда, что все
функции, которые мы будем рассматривать,
равны нулю для отрицательных
![]() (например, вместо
(например, вместо
![]() будем писать 1, вместо
будем писать 1, вместо![]() - просто
- просто![]() и
т.д.).
и
т.д.).
Пример:
Проверить, являются ли функции
![]() ,
,![]() ,
,![]() оригиналами.
оригиналами.
Решение:
Функция
![]() является оригиналом, так как все условия
выполнены:М
= 3,
является оригиналом, так как все условия
выполнены:М
= 3,
![]() ;
функция
;
функция![]() не является оригиналом, так как в точкеt
= 3 имеет
разрыв функции второго рода; функция
не является оригиналом, так как в точкеt
= 3 имеет
разрыв функции второго рода; функция
![]() не является оригиналом, так как
не является оригиналом, так как
![]() для
любых M,
s
и t
> 0.
для
любых M,
s
и t
> 0.
