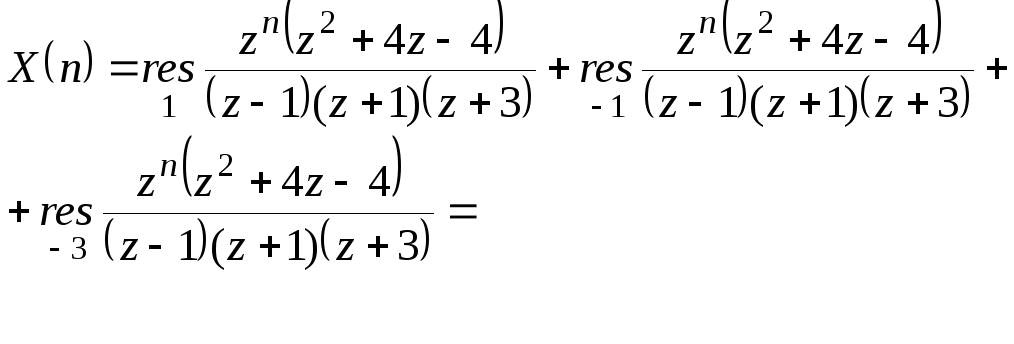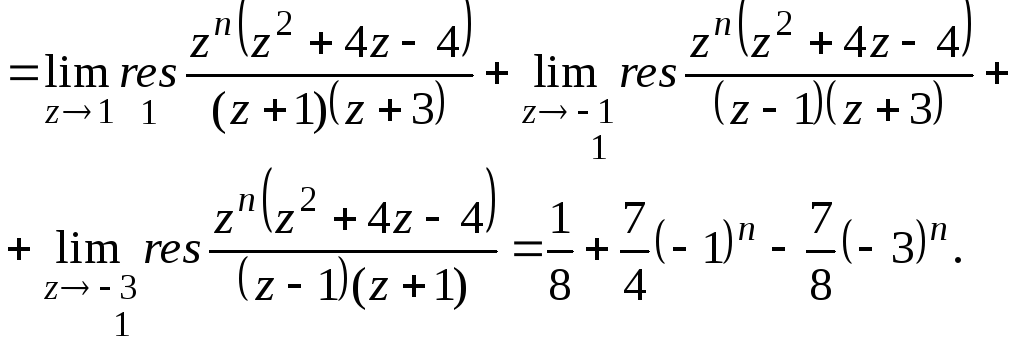1С) Теорема линейности.

Линейность D – преобразования.

2с) Смещение в области оригиналов.

Если , то

и .

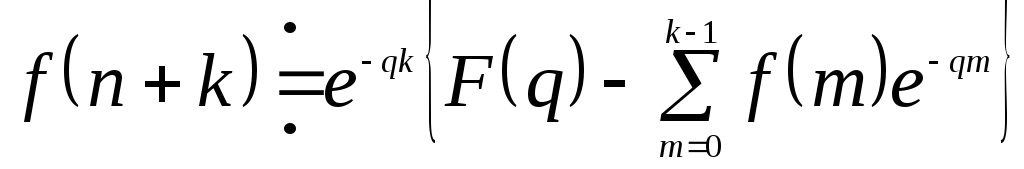3с) Теорема затухания.

Смещение в области изображений.

Если , то

.

Эти свойства доказываются непосредственным применением формулы D – преобразования.

4с) Теорема о разности решетчатой функции.

Изображение конечных разностей.

Если , то

Доказательство:

ч.т.д.

Если функция допускаетD – преобразование, то её разность произвольного порядка к также допускает D – преобразование, поскольку разность представима в виде линейной комбинированной решетчатой функции,.

Многократно применяя предыдущую формулу нетрудно получить

,…

.

Последняя формула значительно упрощается, если решетчатая функция обращается в ноль при n=0,1,…, к-1:

.

5с) Теорема о сумме решетчатой функции.

Изображение конечной суммы.

Если , то

.

Пусть , т.к., то применяя теорему о разностит.о.

.

6с) Дифференцирование изображений.

Если , то

Доказать можно дифференцированием ряда выражающего D – преобразование.

,

7с) Интегрирование изображений.

Если и, то существует интеграл от изображения, определяемый равенством

.

8с) Умножение изображений.

Определим свертку решетчатых функций икак решетчатую функцию, определяемую формулой

Если , то.

Произведению изображений соответствует свертка оригиналов.

9с) Умножение оригиналов.

Если и, то

.

Произведению оригиналов соответствует свертка изображений.

10с) Предельные значения изображений и оригиналов.

а) Если и изображение первой разности является аналитической функцией в правой полуплоскости и на мнимой оси, то справедливо равенство

.

б) Если , то начальное значениеопределяется по формуле

.

Обращаем внимание, что подобные свойства рассмотрены и для непрерывного преобразования Лапласа.

12. РЕШЕНИЕ РАЗНОСТНЫХ УРАВНЕНИЙ

Всякое соотношение, связывающее решетчатую функцию и её разности до некоторого порядка к

(12.1)

называется разностным уравнением.

Используя формулу, выражающую разности различных порядков через значения решетчатой функции

можно соотношение (12.1)преобразовать к виду

(12.2)

Если (12.2) содержит в явном виде функции и, то исходное разностное уравнение (12.1) называют уравнением порядка к.

При переходе от разностей решетчатых функций к самим решетчатым функциям могут взаимно уничтожаться как функции , так и функции. И в результате порядок разностного уравнения может отличаться от порядка старшей разности.

Например.

Дано уравнение

.

Используя выражение для разностей, имеем

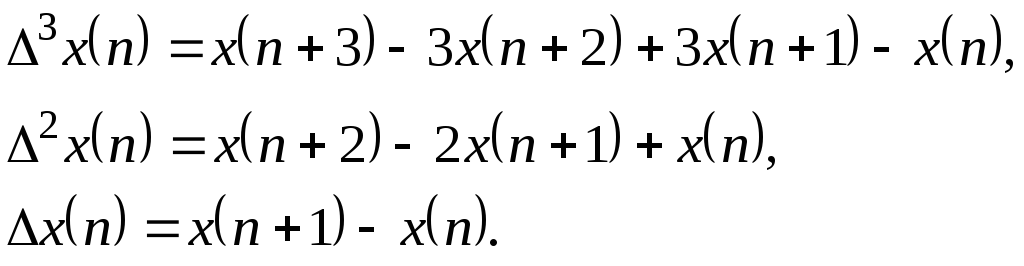
Подставляем в уравнение, после приведения подобных членов получим.

.

Введем новую переменную m=n+1. Получим

.

Т.о. исходное уравнение является уравнением второго порядка, несмотря на то, что оно содержит разность третьего порядка.

Решетчатая функция , которая обращает уравнение в тождество, называется решением разностного уравнения.

Мы ограничимся рассмотрением лишь линейных разностных уравнений к – го порядка с постоянными коэффициентами

(12.3)

Если , то уравнение называется однородным.

Пусть заданы значения - начальные значения. Применяя к обеим частям уравнения (12.3) дискретное преобразование Лапласа и пользуясь свойством 2 – смещение в области оригиналов (теорема опережения), получим уравнение относительно- изображения искомой функции. Решаем это алгебраическое уравнение относительно. Далее, пользуясь таблицами или формулами обратного преобразования, получим.

Если начальные значения не заданы, то, считая их произвольными постоянными получим общее решение уравнения (12.3).

Если исходное линейное разностное уравнение записано в виде

(12.4)

то метод его решения остается тем же. Но для перехода от оригинала к изображению в левой части уравнения следует воспользоваться свойством 4 – изображением конечных разностей. При этом должны быть заданы начальные значения

Если эти значения не заданы, то, считая их произвольными постоянными, получим общее решение.

Указанный метод применяется и при решении систем разностных уравнений.

Пример 1.

Найти решение уравнения

при начальных условиях

.

Решение:

Пусть

Подставляем в уравнение

.

Откуда находим .

.

Удобно произвести замену .

тогда оригинал:

В таблице 3 приведены наиболее часто встречающиеся в примерах соответствия при D-преобразовании и Z - преобразовании.

Пример 2.

Найти решение уравнения при начальных условиях,.

Решение. Здесь уравнение дано в форме разности. Применяем Z – преобразование к обеим частям уравнения:

Откуда,

Таблица 3

№
1.	1
2.
3.
4.
5.
6.	Линейность
7.	Опережение
8.	Запаздывание
9.	Дифференцирование изображения

Решая это уравнение относительно , получим:

.

Возвращаемся к оригиналу:

Пример 3. Найти решение уравнения x(n+2)+4x(n+1)+3x(n)=1, при начальных условиях x(0)=1, x(1)=1.

Решение.

Применяем Z – преобразование к обеим частям уравнения:

откуда получаем:

Возвращаясь к оригиналу, получим: