
- •Введение
- •1. Понятие оригинала
- •2. Изображение по лапласу
- •3. Изображения простейших элементарных функций
- •4.Свойства преобразования лапласа
- •2С) Теорема подобия
- •3C) Теорема затухания (Теорема смещения)
- •5C) Теорема опережения.
- •10С) Интегрирование изображений.
- •11С) Теорема умножения изображений (теорема Бореля)
- •12С) Умножение оригиналов.
- •5.Примеры нахождения изображений с помощью таблиц 1 и 2
- •6. Импульсные функции и их изображения
- •7.Формула обращения преобразования лапласа
- •1)Тождественные преобразования и применение таблиц 1 и 2.
- •2) Вычисление оригиналов с помощью вычетов.
- •8.Применение преобразования лапласа для решения уравнений и систем
- •8.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.2 Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.
- •8.3 Решение дифференциальных уравнений с переменными коэффициентами.
- •8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.5 Линейные дифференциальные уравнения с запаздывающим аргументом.
- •8.6 Интегральные уравнения типа «свертки».
- •8.7 Линейные интегро-дифференциальные уравнения.
- •9.Решение диференциальных уравнений в частных производных и задач математической физики
- •10. Применение операторных методов для анализа линейных систем
- •11. Дискретное преобразование лапласа. Z – преобразование лорана
- •1) Решетчатые функции.
- •2) Конечные разности решетчатых функций.
- •3) Суммирование решетчатых функций.
- •4) Определение дискретного преобразования Лапласа.
- •5) Формула обращения.
- •1С) Теорема линейности.
- •Библиографический список
- •Оглавление
8.Применение преобразования лапласа для решения уравнений и систем
Мы установили соответствия между функциями и операциями в пространствах оригинала и изображения и убедились, что многие сложные операции анализа в пространстве оригиналов превращаются в простые алгебраические операции в пространстве изображений.
Вместо
дифференцирования – умножение на
![]() ,
вместо интегрирования – деление на
,
вместо интегрирования – деление на![]() .
Таким образом вместо дифференциального
уравнения имеем алгебраическое уравнение,
решив которое, получим изображение
решения. Так же и для других задач.
Полученное изображение необходимо
отобразить в пространстве оригиналов,
чтобы получить ответ в приемлемой форме.
.
Таким образом вместо дифференциального
уравнения имеем алгебраическое уравнение,
решив которое, получим изображение
решения. Так же и для других задач.
Полученное изображение необходимо
отобразить в пространстве оригиналов,
чтобы получить ответ в приемлемой форме.
Вообще, под операционным исчислением понимают методы решения задач, основанные на следующих этапах:
от искомых и заданных функций переходят к их изображениям.
над изображениями производят операции, соответствующие заданным операциям над самими функциями.
от найденных изображений решений переходят к оригиналам.
8.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами.
Возьмем неоднородное линейное дифференциальное уравнение второго порядка
![]() (8.1)
(8.1)
и найдем его частное решение при начальных условиях
![]()
Считаем исходную функцию x(t) и правую часть f(t) оригиналами и переходим от уравнения (8.1) связывающего оригиналы к уравнению, связывающему изображения X(p) и F(p).

Изображение уравнения (8.1) будет:
![]() .
.
Мы получили уже не дифференциальное, а алгебраическое уравнение относительно X(p).
![]() .
.
Откуда получим операторное решение д.у.
 .
.
Найдено изображение искомого решения. Теперь по таблицам или формулам обращения найдем x(t).
Если начальные условия нулевые, то операторное решение будет иметь простой вид:
![]()
Пример. Найти решение уравнения
![]()
при нулевых начальных условиях.
Решение:
x(t)=X(p):
![]() .
.
![]()
![]()
![]()
1)![]()
2)![]()
3)![]()
Тогда
![]()
Изложенный метод применим к решению линейного дифференциального уравнения любого порядка.
Пример.
![]()
Решение.
Составим операторное уравнение.
![]()
![]() .
.
Здесь полюса 3х кратные комплексно – сопряженные. Поэтому найдем только вычет в точке i.
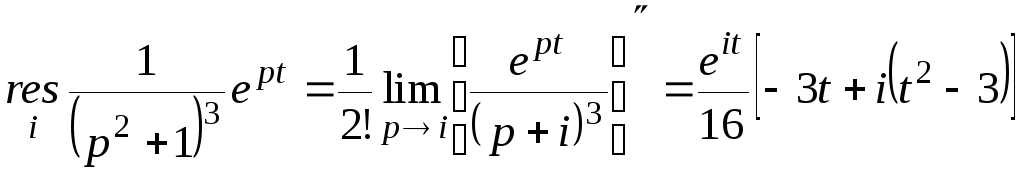
Взяв, удвоенную действительную часть полученного выражения, находим
![]()
Покажем, как следует поступать, если начальные условия заданы не в нулевой точке.
Пример.
Решить уравнение
![]() ,
при начальных условиях
,
при начальных условиях
х(1)=1 х/(1)=0.
Решение:
введем новую переменную
![]() ,
положив t=
,
положив t=![]() +1,
тогда при
+1,
тогда при
![]() .
.
x(t)=x(![]() +1)=
+1)=![]() .
.
Теперь уравнение и начальные условия перепишутся в виде:
![]()
Пусть
![]() =Х(р).
=Х(р).
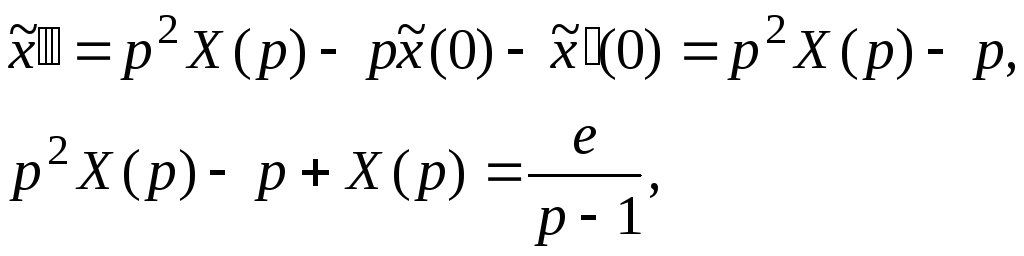
![]()

![]()
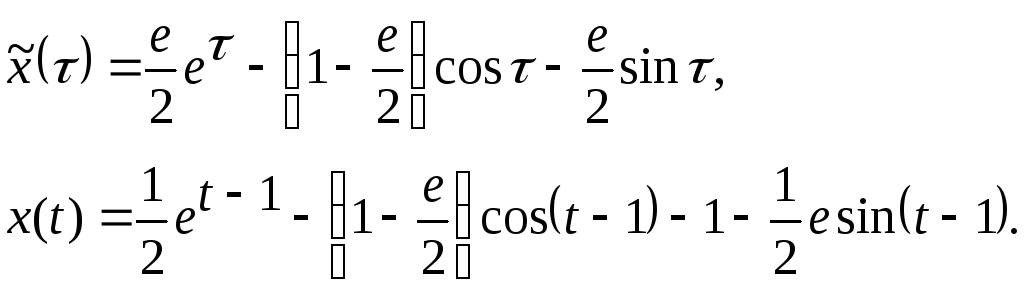
В некоторых случаях правая часть задается в виде комбинации различных аналитических выражений взятых на различных интервалах, или даже графически. Если эта функция является оригиналом, то можно применить операторный метод решения.
Пример. Решить задачу Коши.
![]()
если f(t) задана графически (рис.8.1).
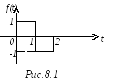
Решение:
Запишем
![]() в аналитическом виде с помощью функции
в аналитическом виде с помощью функции![]() :
:
![]()
Применяя теорему запаздывания, получим
![]() .
.
Пусть x(t)=X(p), получим операторное уравнение.
![]() .
.
Откуда,
![]()
Так
как
![]() .
.
Применяя теперь теорему запаздывания, получим

или
![]() .
.
8.2 Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.
![]() .
.
Пусть требуется решить линейное дифференциальное уравнение с постоянными коэффициентами n-го порядка.
![]() (8.2)
(8.2)
при нулевых начальных условиях.
![]() (8.3)
(8.3)
Пусть нам известно решение уравнения
L(x) = 1, (8.4)
при тех же начальных условиях (8.3).
Это
решение
![]()
Операторное уравнение (8.4) будет иметь вид:
![]() (8.5)
(8.5)
Откуда,
![]() (8.6)
(8.6)
Операторное уравнение (8.2).
X(p)L(p)=F(p). (8.7)
Откуда
![]()
или с учетом (8.6)
![]() (8.8)
(8.8)
Теперь в силу интеграла Дюамеля, получим
![]() .
.
А так как начальные условия нулевые
![]()
где
![]() - решение уравнения с единичной правой
частью. Т.о. зная решение для единичной
правой части, при помощи интегрирования
найдем решение для любой правой части.
- решение уравнения с единичной правой
частью. Т.о. зная решение для единичной
правой части, при помощи интегрирования
найдем решение для любой правой части.
Пример. Найти частное решение уравнения
![]()
при нулевых начальных условиях.
Решение:
Здесь правая часть не является оригиналом
![]() ,
не удовлетворяет третьему условию
оригинала.
,
не удовлетворяет третьему условию
оригинала.
Рассмотрим уравнение:
![]() .
.
Операторное уравнение имеет вид:
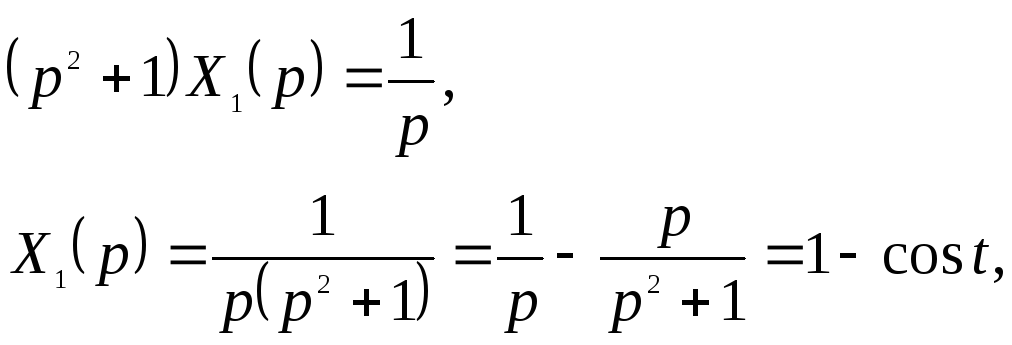
таким
образом
![]() - это решение уравнения при единичной
правой части.
- это решение уравнения при единичной
правой части.
Тогда
![]() .
.
Выразить полученный интеграл с помощью элементарных функций не удается и обычно ищется приближенное решение.
