Analiticheskaya_geom / 1_3_Vektory_v_koordinatakh_Ortonormirovanny_ba

1.3. Лекция 3. Векторы в координатах.

Ортонормированный базис

Базис и координаты. Координатные столбцы векторов. Линейные операции над векторами в координатной форме. Ортонормированный базис. Направляющие косинусы. Скалярное произведение в ортонормированном базисе. Детерминанты второго и третьего порядков. Векторное и смешанное произведения в правом ортонормированном базисе.

В лекции 2 вместо векторов-сил, векторов-скоростей и т.д. мы рассматривали идеальные объекты – свободные геометрические векторы. Это был первый шаг абстрагирования: от физических объектов к геометрическим. В этой главе мы сделаем второй шаг: от геометрических объектов к алгебраическим. Благодаря этому мы получим возможность считать! Действительно, попробуйте-ка сложить по правилу параллелограмма три некомпланарных вектора или, что несравненно сложнее, решить векторное уравнение. Но плата за эту возможность оказывается довольно высока, что будет ясно с позиций тензорного исчисления.

Базис и координаты

Базисом на прямой называется любой ненулевой вектор на этой прямой.

Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов этой плоскости.

Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов.

Представление вектора в виде линейной комбинации некоторых векторов называют его разложением по этим векторам. Как правило, рассматривают разложение вектора по базису.

Если базис в пространстве и

,

то числа , , называют координатами вектора в базисе .

Теорема 3.1. Пусть – базис в пространстве. Тогда любой вектор допускает, притом единственное, представление вида

. (3.1)

Доказательство. Докажем единственность представления (3.1). Допустим, существует другое представление:

.

Тогда

.

Умножим это равенство скалярно на вектор . Получим

.

Так как , то . Аналогично заключаем, что , . Единственность представления (3.1) доказана.

Возможность представления (3.1) доказывается несложным геометрическим построением. Приведем вектора ,,, к общему началу . Для простоты предположим, что вектор образует острые углы со всеми векторами ,,. Вообразим себе параллелепипед, выходящие из точки ребра которого суть продолженные вектора ,,, а большая диагональ, выходящая из точки , – вектор . Тогда равен сумме указанных векторов, представляющих названные ребра. 

Координатные столбцы векторов

Пусть – базис в пространстве и

, .

Столбцы

,

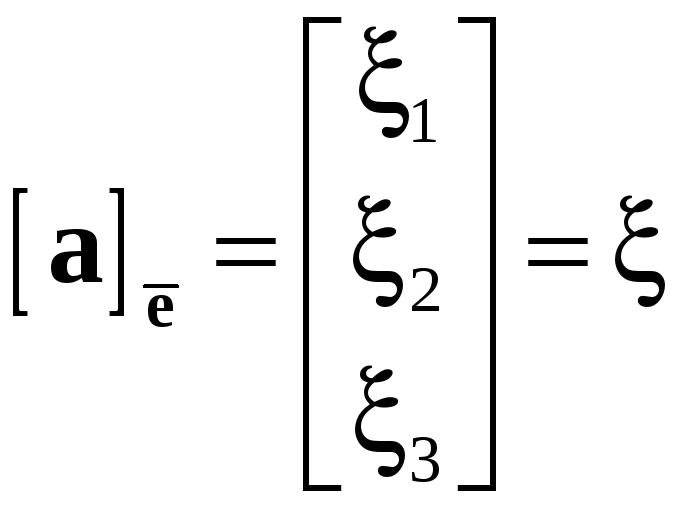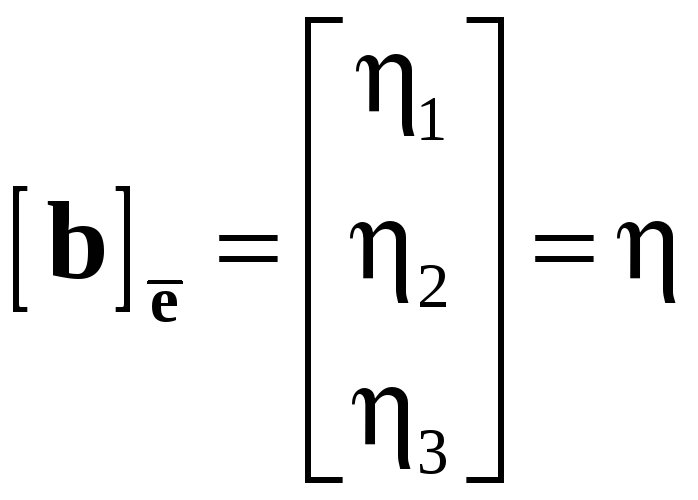
будем называть координатными столбцами векторов , в базисе . Множество всех таких столбцов обозначим через . Отображение

, (3.2)

как следует из предыдущей теоремы, устанавливает (при фиксированном базисе) взаимно однозначное соответствие между множеством всех свободных векторов и множеством . Это отображение, оказывается, обладает чрезвычайно важной особенностью – является изоморфизмом. Обсудим это.

Из алгебраических свойств линейных операций над векторами следует

.

Тогда

(3.3)

Аналогично проверяется, что

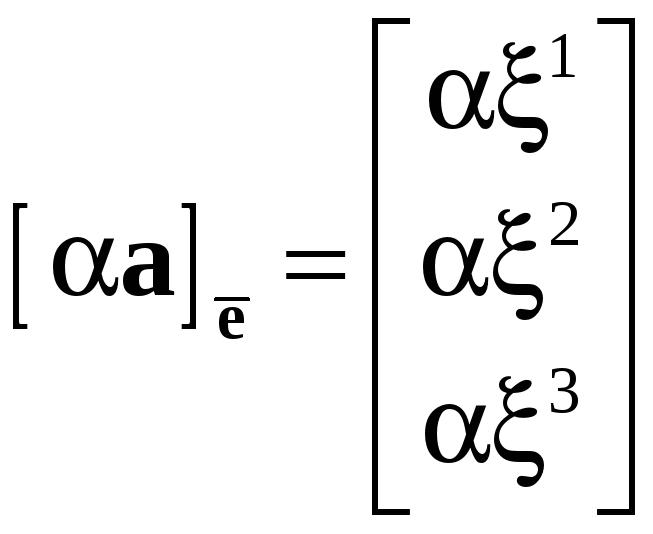. (3.4)

Введем на операции сложения столбцов и умножения столбцов на числа:

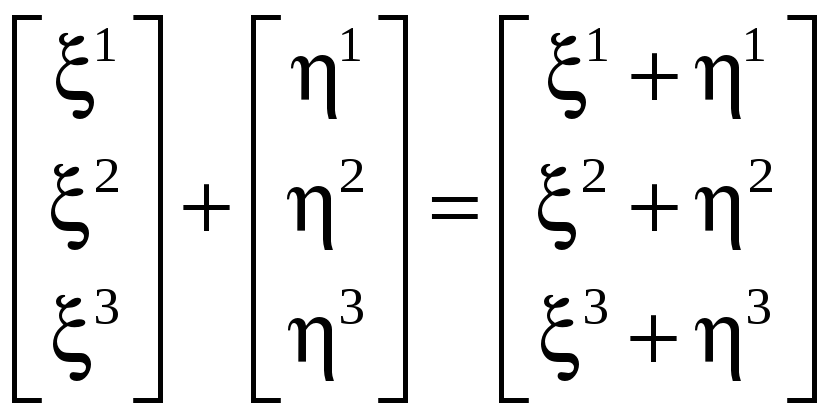, (3.5)

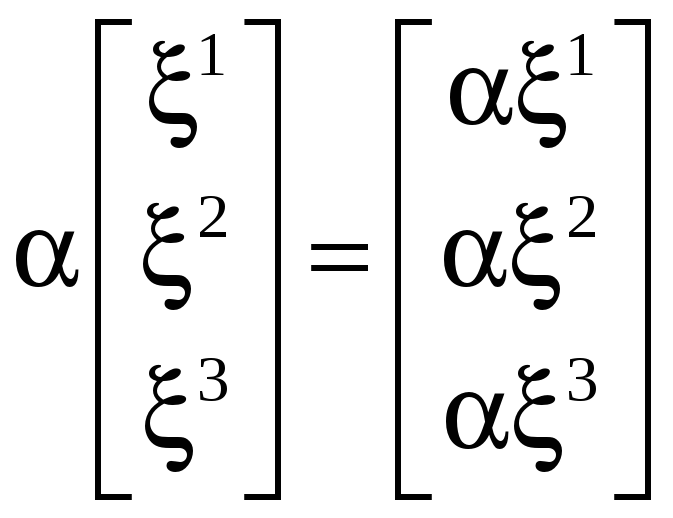. (3.6)

Теперь (3.3), (3.4) можно переписать в виде

, . (3.7)

Иными словами, отображение удовлетворяет условиям:

, , (3.8)

т. е. является изоморфизмом линейных пространств.

Упражнение 3.1. Докажите тождество

.

Изоморфизм позволяет вместо геометрической системы изучать арифметическую систему . Так, например, (3.5) есть алгебраическое выражение геометрического правила параллелограмма сложения векторов.

Ортонормированный базис

Базис называется ортонормированным, если

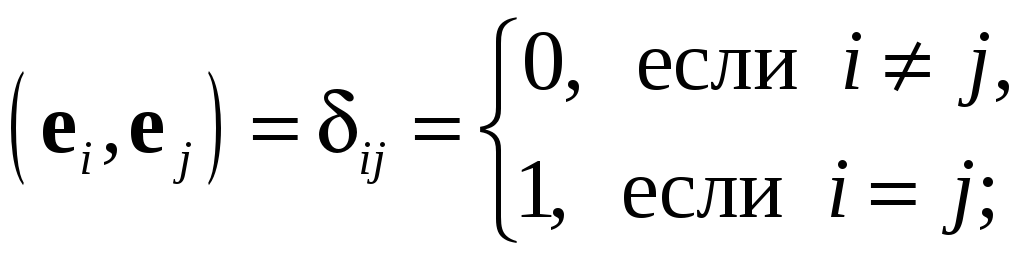
(3.9)

Из определения скалярного произведения следует, что базис ортонормирован тогда и только тогда, когда его вектора имеют единичную длину и попарно ортогональны. Геометрический смысл координат вектора в ортонормированном базисе проясняет следующее

Предложение 3.1. Пусть – ортонормированный базис и . Тогда

,

где , т. е. есть прямоугольная проекция вектора на ось вектора , .

Доказательство. По определению скалярного произведения

.

С другой стороны, из алгебраических свойств скалярного произведения и ортонормированности базиса следует



Косинусы называют направляющими косинусами вектора .

В ортонормированном базисе скалярное произведение имеет очень простой вид.

Теорема 3.2. Пусть – ортонормированный базис и , Тогда

Доказательство. Используя алгебраические свойства скалярного произведения, получим

=



Следствие 3.1.

Доказательство. 

Следствие 3.2.

Доказательство следует из определения скалярного произведения как и только что полученных координатных представлений скалярного произведения и модуля вектора. 

Упражнение 3.2. Получите следующую формулу для направляющих косинусов вектора:

.

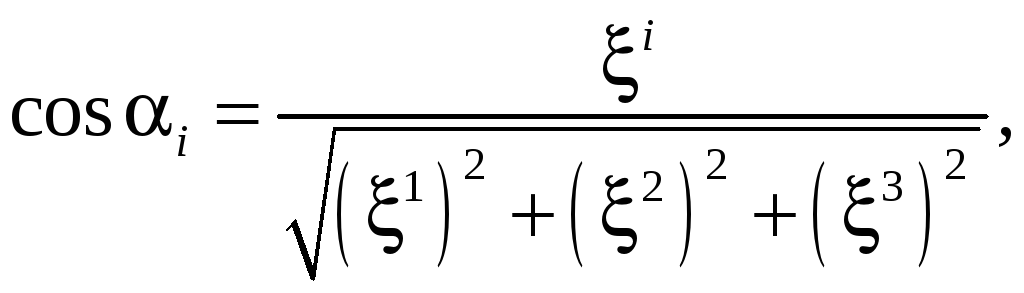
Упражнение 3.3. Докажите тождество для направляющих косинусов вектора

.

Вектор, сонаправленный вектору и имеющий единичную длину, называется ортом вектора и обозначается .

Упражнение 3.4. Докажите, что 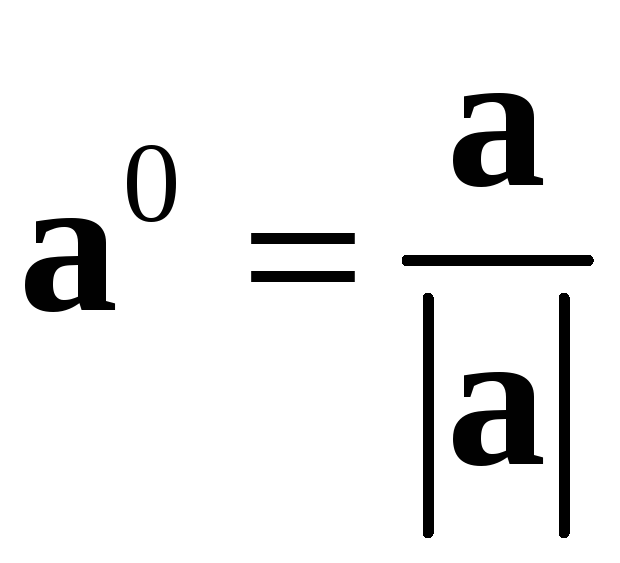и координаты вектора совпадают с направляющими косинусами вектора .

Предложение 3.2. Если – правый ортонормированный базис, то

, , ,

.

Доказательство непосредственно следует из ортонормированности базиса и определений векторного и скалярного произведений. 

Обычно используют правый ортонормированный базис.

Теорема 3.3. Пусть – правый ортонормированный базис и , Тогда

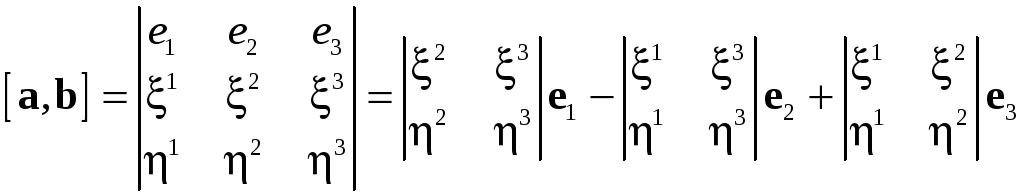. (3.10)

Доказательство. Из алгебраических свойств векторного произведения и предложения 3.2 следует

. 

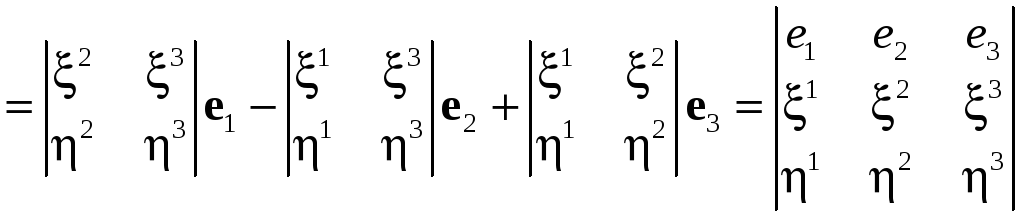Теорема 3.4. Пусть – правый ортонормированный базис и , , . Тогда

.

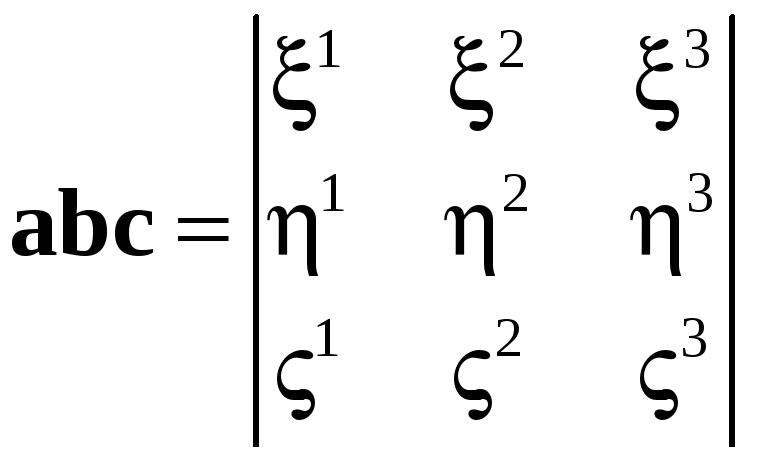Доказательство. По определению смешанного произведения . Умножая скалярно обе части равенства (3.10), получим требуемое. 

Следствие. Вектора , , компланарны тогда и только тогда, когда

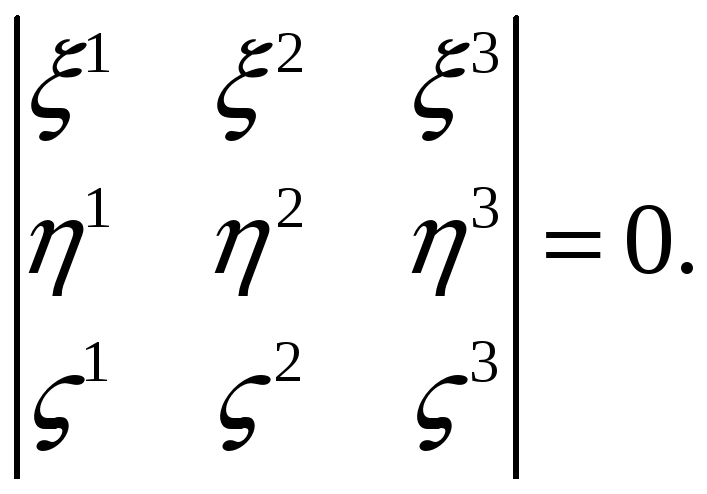
Вычислив формулу (3.6) из лекции 2 в координатах, получим следующее тождество Лагранжа:

.

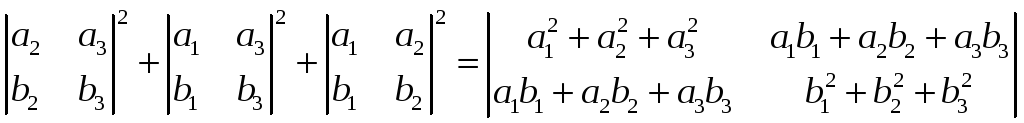Разлагая векторы , , по ортонормированному базису, с помощью теоремы об умножении определителей нетрудно получить уже встречавшееся тождество

.

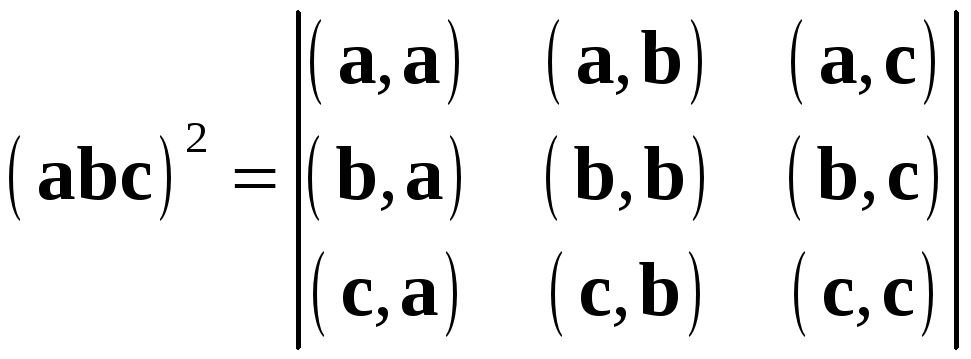Упражнения

3.1. Как выглядит множество точек плоскости, у которых координаты точек удовлетворяют неравенству для некоторого ? Как выглядит множество ?

3.2. Найти ортогональную проекцию вектора на прямую, направление которой определяется вектором , и ортогональную составляющую вектора относительно этой прямой. Найти орт вектора и его направляющие косинусы. Сделать чертеж.

3.3. Даны два вектора и . Найти вектор , удовлетворяющий системе уравнений , . Найти орт вектора и его направляющие косинусы.

3.4. Векторы , и и имеют равные длины и образуют попарно равные углы. Найти координаты вектора , если , . Найти орт вектора и его направляющие косинусы.

3.5. Даны векторы , , . Вычислить и .

3.6. Даны вершины треугольника , , . Вычислить его высоту, опущенную из вершины .

3.7. Раскрыть скобки и упростить .

3.8. Сила приложена к точке . Определить момент силы относительно начала координат, его величину и направляющие косинусы.

3.9. Доказать, что площадь выпуклого многоугольника на плоскости с вершинами равна половине абсолютной величины выражения

.

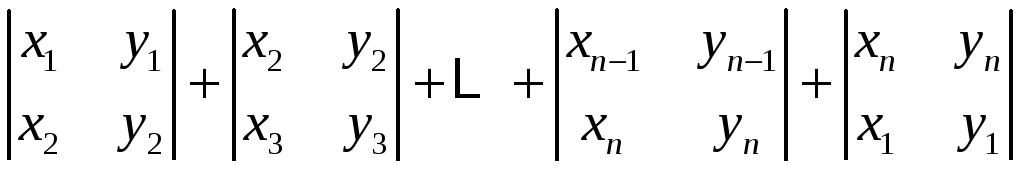Вопросы для самопроверки

1. Что такое базис на плоскости и в пространстве?

2. Существует ли направление в пространстве, составляющее с осями координат прямоугольной системы, углы по градусов?

3. Задайте два вектора своими координатами и найдите их скалярное произведение.

4. Задайте детерминанты второго и третьего порядков и вычислите их.

5. Задайте два (три) вектора их координатами и найдите их векторное (смешанное) произведение.

252