2. v′y = u′x = 2sh2x cos 2 y; v = 2sh2x∫cos 2 ydy = sh2x sin 2 y +C(x).

Из 2-го условия К – Р:

′

′

C = const.

2ch2x sin 2 y + C ( x) = 2ch2x sin 2 y

C ( x) = 0

f (z) = ch2x cos 2 y + i sh2x sin 2 y = ch(2x + 2iy) = ch2z.

Вопросы для самопроверки.

1.

Являются ли следующие множества точек областями?

1) 2 <

z −3

< 4; 2) 0 < arg z <π / 3; 3)

z

<1∩

z

≥ 3; 4) 0 < Im z ≤1;

2.

Записать комплексные числа в тригонометрической и показательной форме.

1) z = −3; 2) z = 2i; 3) z = 3 −4i;

3.

Доказать тождество:

ch2 z −sh2 z =1.

4.

Является ли функция

f (z) = z Re z аналитической?

2 Интегральное исчисление функций комплексной переменной.

2.1 Интегралы в комплексной области.

Пусть функция f (z) = u(x, y) + iv(x, y) непрерывна в области G ,

а L – гладкая кривая,

лежащая в этой области, заданная уравнением z(t) = x(t) + iy(t) , α ≤ t ≤ β ; z(α) = A, z(β) = B.

Кривую будем считать ориентированной, если заданы начальная и конечная точки кривой. При этом, положительное направление задается изменением параметра t от меньшего значения к большему (т.е. А – начало кривой, В – конец ).

Напомним, что кривая называется гладкой, если у нее существует непрерывная касательная в

каждой точке, что эквивалентно наличию непрерывных производных	′	′
	x (t)	u y (t), t [α, β],

не равных нулю одновременно. Необходимо сделать замечание относительно ориентации замкнутых кривых, так как начальная и конечная точки в этом случае совпадают. Если замкнутый контур без самопересечений целиком лежит в некоторой области, то обход контура называют положительным при движении против часовой стрелки.

При этом контур обозначают Г+ или просто Г (по умолчанию). В противном случае ориентация контура называется отрицательной и обозначается Г− . Если же контур является границей области, то его обход называется положительным в том случае, когда область при

движении остается слева.	Например, положительный обход области					z −2		< 3 идет против
часовой стрелки, а области		z −2		> 3 − по часовой. По умолчанию, обход области по границе

всегда будем считать положительным.

Определение. Интегралом от функции комплексной переменной по кривой L называется:

I = ∫ f (z)dz = ∫(u + iv)(dx + idy) = ∫(udx −vdy) + i∫(vdx +udy) .

L L L L

Таким образом, интеграл от комплексной функции равен сумме двух криволинейных интегралов

второго рода (см. курс «Теория поля»), которые, в свою очередь, сводятся к вычислению двух

						β
							′	′
	обыкновенных интегралов: I = ∫[u(x(t), y(t))x (t) −v(x(t), y(t)) y (t)]dt +
						α
		β					β
					′	′	′
	+ i∫[u(x(t), y(t)) y (t) + v(x(t), y(t))x (t)]dt						= ∫ f (z(t))z (t)dt.
		α					α
	Примеры. Вычислить интегралы:
		∫					1		i
	1.			zdz ; ( AB) : y = x2 ,0 ≤ x ≤1. Решение. I = ∫(x + 2x3 )dx + i x2dx =1 +						.
		( AB)					0	3
	2.	∫	1		dz и	∫(z − z0 )n dz (n Ν)	по окружности L	радиуса R с центром в т. z0 .
			z − z
		L		0		L

Решение. Запишем уравнение окружности в виде:

- 9 -

z − z0

= R ei t , 0 ≤ t < 2π (ясно, что

z − z0

= R t, те. . L − окружность). Отсюда:

dz

2π

it

2π

1) ∫

= ∫

R i eit dt

= i ∫ dt = 2πi .

z − z0

L

0

R e

0

2π

e

i(n+1)t

2π

2) ∫(z − z0 )n dz = ∫ Rn+1 i ei(n+1)tdt = i Rn+1

= 0.

i (n +1)

L

0

0

Замечание. Значение интегралов во втором примере не зависят от радиуса окружности.

2.2 Теория интегрирования Коши.

Примеры предыдущего пункта во-первых показывают существенное отличие интегрирования в комплексной области от интегрирования в действительной и во-вторых легко обобщаются. Теорема Коши. Пусть f (z) − аналитическая функция в односвязной области D , а Г − любой

кусочно – гладкий замкнутый контур, принадлежащий этой области. Тогда интеграл от функции f (z) по контуру Г равен нулю: ∫ f (z)dz = 0.

Г

Доказательство. Так как f − аналитическая функция, то ее действительная и мнимая части удовлетворяют условиям Коши – Римана: u′x = v′y , u′y = −v′x , откуда сразу следует, что

подынтегральные выражения udx − vdy и vdx + udy (п.2.1) представляют собой полные дифференциалы (см. ФНП) и, следовательно, соответствующие криволинейные интегралы по замкнутому контуру (см. ТП) равны нулю ∫ f (z)dz = 0. (Пример 2.2 §10).

Г

Доказанная теорема легко обобщается на многосвязные области.

Теорема. Пусть функция f (z) – аналитическая в многосвязной области D , ограниченной ориентированным контуром Г. В этом случае ∫ f (z)dz = 0.

Г

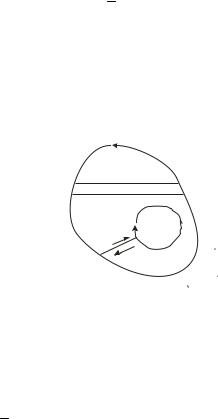
Доказательство (для двусвязной области (Рис.2)):

Область D ограничена контуром Г = Г1 + Г2 , ориентированным

в положительном направлении. Соединим контуры Г1 и Г2 линией γ. Ориентируем
способами:	γ+ и γ− . В результате получим односвязную область,
ограниченную контуром Г1 +γ + + Г2 +γ −. По теореме Коши
∫	f (z)dz = 0. Так как ∫ fdz + ∫ fdz = 0, получаем:
Г1 +γ + +Г2 +γ −	γ +	γ −

γ двумя

Г1

n+1

D

∫ fdz = ∫ fdz + ∫ fdz = 0. В общем случае ∫ fdz = ∑∫ fdz = 0.

+

Г

Г1

Г2

Г

k =1 Гk

γ

− Г2

При этом, каждый из интегралов ∫ f (z)dz может быть и не равным

γ

нулю.

Гk

Рис.2

Обозначим буквой Г

кусочно – гладкий замкнутый контур,

ориентированный против часовой стрелки, а тот же контур, ориентированный по часовой стрелке − символом Г− (в этих обозначениях в последней теореме следовало бы писать Г1 и

Гk−, k >1 ).

Следствие. Пусть область D ограничена внешним контуром Г и внутренними контурами Г1, … , Гn . В последних обозначениях, для аналитической на D функции имеет место

n

равенство: ∫ fdz = ∑∫ fdz.

Гk =1 Гk

Доказательство.		В указанных	обозначениях утверждение теоремы		имеет вид:
	n		n	n
∫ fdz + ∑∫ fdz = 0. Отсюда: ∫ fdz = −∑∫				fdz = ∑∫ fdz.
Г	k =1 Гk−	Г	k=1 Гk−	k =1 Гk

- 10 -

Замечание. Из полученных результатов следует, что примеры п.2.1 верны для любого кусочно –

непрерывного замкнутого контура Г, содержащего точку z0 : ∫	dz	= 2πi и	∫(z − z0 )n dz = 0.
	z − z
Г	0		Г
2.3 Формула Коши.
Пусть функция f (z) является аналитической в односвязной области G, а			z0 – произвольная
внутренняя точка этой области. Построим замкнутый контур	Г G и содержащий эту точку.

G

D

			Рис.3
	∫	f (z)	dz = i 2∫π
		z − z0
	γ		0

Г	Рассмотрим вспомогательную функцию	ϕ(z) =	f (z)	. Эта
			z − z0

функция регулярна во всех точках области D ограниченной контуром Г, за исключением т. z0. Проведем окружность γ с

γцентром

в т. z0 радиуса ρ, целиком принадлежащую области D. Если оба

ρ.z0 контура ориентировать против часовой стрелки, то будет иметь

	место равенство: ∫	f (z)	dz = ∫		f (z)	dz (п.2.2). Так как левая
	Г	z − z0		γ	z − z0
	часть равенства не зависит от			ρ, то и правая от ρ не зависит. На
	контуре γ z = z0 + ρeit и интеграл в правой части будет равен:
2π	2π		2π
f (z)dt =i ∫	[ f (z) − f (z0 )]dt + i ∫ f (z0 )dt = i ∫[ f (z) − f (z0 )]dt + 2πif (z0 ).
0	0	0

Подынтегральная функция в последнем интеграле стремится к нулю при ρ →0 , а сам интеграл

от ρ не зависит. Отсюда сразу следует, что этот интеграл равен нулю (если предел постоянной

– ноль , то постоянная равна нулю). Окончательно получаем формулу Коши:

	f (z)	dz = 2πi f (z0 )	(2.1)
∫Г z − z0

Формулу Коши можно написать для произвольной точки z0 G , не принадлежащей контуру Г:

1	∫Г	f (z)	dz =	f (z0 ), z0 − внутри Г
				0 , z0 − вне Г
2πi		z − z0

(равенство нулю сразу следует из теоремы Коши (п.2.2)).

Выражение, стоящее в левой части последней формулы, называют интегралом Коши.

2.4 Следствия интегральной формулы Коши.

Рассмотрим односвязную область G , ограниченную замкнутым контуром Г. Пусть задана функция ϕ(z,ζ ) , z G,ζ Г , удовлетворяющая следующим условиям:

1. ϕ(z,ζ ) для ζ Г является аналитической функцией переменной z в области G.

2. Функции ϕ(z,ζ ) и ∂ϕ(z,ζ ) непрерывны по совокупности переменных z и ζ z G ,ζ Г .

∂z

В этом случае существует функция F(z) = ∫ϕ(z,ζ ) dζ как интеграл, зависящий от параметра z,

Г

определенная для z G .

Можно доказать, что при указанных предположениях F(z) является аналитической функцией комплексной переменной z во всей области G , причем производную этой функции можно вычислять под знаком интеграла.

- 11 -

Рассмотрим теперь произвольную замкнутую подобласть

G ,

расстояние от всех точек

D

которой до границы Г

больше некоторого положительного числа

d :

z −ζ

≥d. Функция

ϕ(z,ζ ) =

f (ζ )

, где f (z)

− функция, аналитическая в области G , удовлетворяет условиям (1)

ζ − z

и (2) z G . В свою очередь, функция f(z) во всех точках области D представляется

интегралом Коши: f (z) =

1

∫

f (ζ )

dζ (формула (2.1)). Пользуясь предыдущим утверждением,

2πi

Г

ζ − z

вычислим ее производную с помощью дифференцирования под знаком интеграла:

′	1	∫Г	f (ζ )
f (z) =				dζ .
	2πi		(ζ − z)2

Повторяя данные рассуждения, окончательно получим:

Аналитическая в области G функция бесконечно дифференцируема в этой области, а ее производные удовлетворяют соотношению:

f

(n)

(z) =

n!

∫Г

f (ζ )

dζ или

∫Г

f (z)

dz =

2πi

f

(n)

(z0 ) .

2πi

(ζ − z)n+1

(z − z0 )n+1

n!

Полученные формулы часто используются при вычислении интегралов.

Пример. Вычислить интегралы: ∫

sin z dz и

∫

shz

dz .

2

z−1

=2

z + i

z+1

=3

(z −1)

Решение.

1. Точка

z = − i лежит внутри данной окружности, а функция f (z) = sin z , поэтому

∫

sin z dz =

2πi sin(−i) = 2πsh1 .

z−1

=2

z + i

shz

2πi (shz)′

2.

∫

dz =

z=1 = 2πich1.

2

z+1

=3 (z −1)

1!

Можно вычислять интегралы и в том случае, когда подынтегральная функция имеет несколько указанных особенностей в точках, лежащих внутри контура интегрирования, используя следствие теоремы Коши (§11). При этом необходимо учитывать, что регулярные части функции будут отличаться друг от друга в каждой особой точке.

Пример. ∫

shz

dz = ∫

shzdz

+ ∫

shzdz

shz

shz

= 2πi

+

= 2πi sin1.

2

z+1

=3

z

+1

γ1

(z − i)(z + i)

γ2

(z − i)(z + i)

z + i

z=i

z − i

z=−i

2.5Ряды Тейлора и Маклорена.

Вп.1.6 были введены понятия рядов Тейлора и Маклорена функции f(z). Рассмотрим теперь более подробно свойства этих рядов. Для определенности, будем рассматривать только ряды

Тейлора. Итак, пусть функция f(z) равна сумме некоторого степенного ряда в области его

∞

сходимости:

f (z) = ∑cn (z − z0 )n ,

z − z0

< R.

Так

как

степенной

ряд равномерно сходится в

n=0

D (D − область сходимости) , то f(z)

является непрерывной ,

любом замкнутом круге K

бесконечно

дифференцируемой

функцией

(

как

сумма

непрерывных и

бесконечно

дифференцируемых функций). Отсюда сразу следует,

что f(z) −

аналитическая функция в

. Имеет место и обратное утверждение:

указанной области K

Теорема Тейлора. Функция

f(z) , аналитическая

внутри

круга

z − z0

<R ,

может быть

∞

однозначно представлена в этом круге сходящимся степенным рядом

f (z) = ∑cn (z − z0 )n .

n=0

- 12 -