Интегрирование по частям и признаки условной сходимости.

Рассмотрим , где- непрерывна на,.

Пусть – первообразная, тогда

Если существует - конечный и существует- сходящийся, то существует, то есть интеграл сходящийся.

Первый признак сходимости (Абеля).

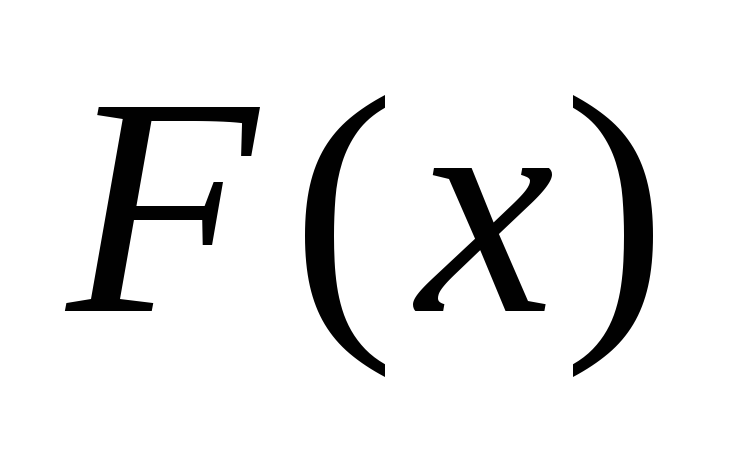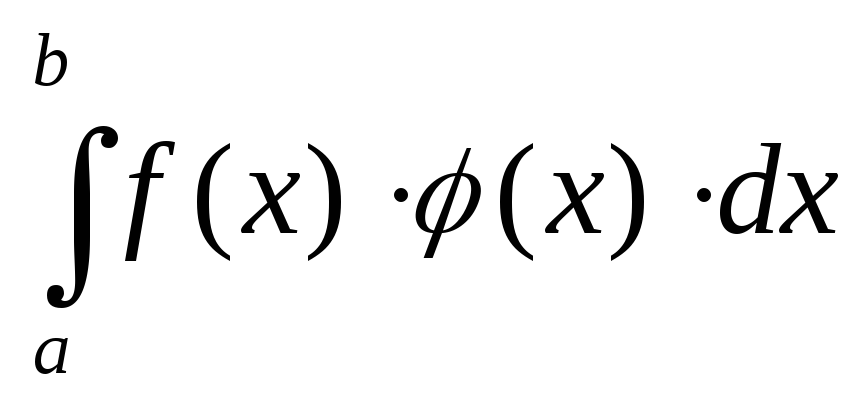Если ограничена на,и- сходящийся абсолютно, то- сходящийся.

Доказательство:

Рассмотрим

Рассмотрим , он абсолютно сходящийся:

- сходящийся по условию. Значит интеграл сходится.

Признак Дирихле.

Если - ограниченная на, знакопостояннаямонотонно стремится к 0 при, то интеграл сходящийся.

Доказательство:

Так как - знакопостоянная, то меняя знак, мы всегда можем добиться того, чтобы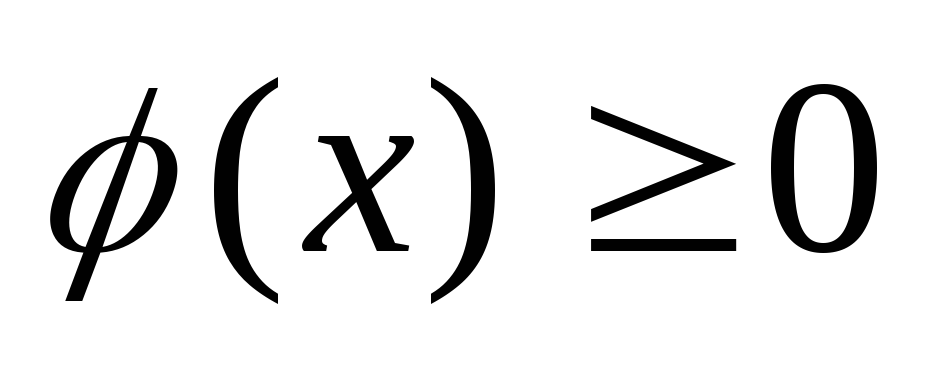. Рассмотрим этот случай.

Очевидно,

Надо доказать, что – сходится. Рассмотрим случай, с учетом невозрастания, тогда

- сходится, тогда исходный интеграл сходящийся по первому признаку.

Пример. Исследуем на сходимость

- сходящийся.

- расходящийся, а - сходящийся по признаку Дирихле, значит и весь исходный интеграл расходится. Таким образом,сходится условно.

Гамма-функция Эйлера.

Рассмотрим интеграл.

1) n=1

Далее рассмотрим интеграл

Положим . Исходя из предыдущего, если- натуральное, то

Докажем корректность( то есть, что интеграл сходится):

Если, то единственная особенность в точке.

- две особенности: 0; .

Чтобы сразу захватывать оба случая, рассмотрим интеграл отдельно на двух промежутках.

- сходится вне зависимости от .

Рассмотрим этот интеграл при

интеграл сходится.

Таким образом, исходный интеграл сходится при любом положительном .

При доказательстве того, что

у нас получилось свойство:

. В доказательстве не было существенно, какое n.

Если в доказательстве этого равенства вместо поставить произвольное положительное, ничего не изменится, следовательно, мы получим свойство гамма-функции:

Таким образом, гамма-функция Эйлера – обобщение понятие факториала на все положительные числа.