2.6. Оценка точности по материалам уравнивания
Для оценки точности результатов измерений вычисляют
(18)
- среднюю квадратическую ошибку единицы веса.
(19)
- обратный вес функции, определяемый в дополнительном столбце схемы решения нормальных уравнений (табл. 2), вычисляется как сумма [πff] и произведений чисел элиминационных строк столбца F на вышестоящие числа того же столбца.
(20)
- средняя квадратическая ошибка функции.
2.7. Блок-схема коррелатного способа уравнивания
1. Анализируют совокупность измерений, определяют число t необходимых и r избыточных измерений. Устанавливают систему весов измерений.
2. Составляют независимые условные уравнения связи в количестве r = n - t. Если r < n - t, после уравнивания останутся невязки. Если r > n - t, лишние уравнения будут зависимы и определитель системы нормальных уравнений будет равен нулю.
3. Условные уравнения связи приводят к линейному виду, вычисляют коэффициенты и свободные члены (невязки) условных уравнений поправок.
4. Для оценки точности уравненных величин составляют весовую функцию и линеаризуют ее.
5. Составляют нормальные уравнения коррелат, вычисляют коэффициенты; свободные члены - невязки условных уравнений поправок. Для последующей оценки точности вычисляют величины [πaf], [πbf], ..., [πrf], [πff].
6. Решают нормальные уравнения, получают коррелаты и контролируют их.
7. Вычисляют поправки к результатам измерений νi, [pv²] и контролируют их: [pv²] = - [kw].
8. Вычисляют уравненные значения измеренных величин и выполняют контроль уравнивания.
9. Вычисляют обратный вес функции.
10. Для оценки точности результатов измерений вычисляют среднюю квадратическую ошибку единицы веса μ. Вычисляют среднюю квадратическую ошибку функции.
2.8. Уравнивание нивелирной сети коррелатным способом
Исходные данные для нивелирной сети, представленной на рис. 1:
НА = 100,000 м; НВ = 110,000 м - отметки исходных пунктов.
h (м): 5,005; 5,015; 5,001 - измеренные превышения.
S (км) : 2; 2; 1 - длины ходов.
pi = c/Si: 0,5; 0,5; 1,0 - веса измерений, с = 1 - постоянная .
Рис. 1. Нивелирная сеть
Определим число независимых условных уравнений.
Уравнивание нивелирной сети начинают с подсчета числа независимых условных уравнений по формуле r = n - t. В сети, представленной на рис. 1, число измеренных превышений n = 3. Число необходимых измерений t = 1 - количеству вновь определяемых пунктов. Таким образом, r = 2.
Составим условные уравнения связи.
В нивелирной сети имеют место полигонные условия: разность суммы превышений в полигоне после уравнивания и теоретической суммы превышений должна быть равна нулю. Выбирают независимые полигоны - замкнутые или разомкнутые, опирающиеся на твердые пункты, в количестве r. На схеме сети показывают номера выбранных полигонов и стрелкой направление суммирования превышений в полигоне. Если направление хода и напрaвление суммирования превышений в полигоне совпадает, знак у превышения "плюс", если не совпадает, превышение следует взять со знаком "минус".
Условные уравнения связи можно записать в форме (4):
Система имеет вид:
(21)
Составим условные уравнения поправок:
Система (21) линейного вида. Для перехода к условным уравнениям поправок достаточно вычислить невязки, которые следует выразить в сантиметрах или миллиметрах, чтобы порядок коэффициентов и невязок был одинаков.
Условные уравнения поправок имеют вид:
(22)
Составим весовую функцию:
F = F(y1 + ν1, y2 + ν2, ..., yn + νn) = f0 + f1ν1 + f2ν2 + ... + fnνn.
В качестве весовой функции целесообразно взять отметку определяемой точки и записать ее математическое выражение через измеряемые превышения от ближайшего исходного пункта.
(23)
Составим нормальные уравнения коррелат:
Коэффициенты условных уравнений поправок
и
весовой функции F = HI = f0 + ν1 поместим по
столбцам (см. табл. 1) в табл. 3. πi = 1/pi -
обратный вес результата измерения.
Таблица 3
Коэффициенты условных уравнений и функции
Решим в схеме Гаусса (табл. 4) полученную систему нормальных уравнений коррелат, обратный вес функции вычислим в дополнительном столбце схемы (см. табл. 2).
Таблица 4
Решение нормальных уравнений коррелат
Следует иметь в виду, что количество запасных знаков, оставляемых при решении нормальных уравнений, зависит от точности невязок w и соответствует представленному в данном примере.
Вычислим поправки к результатам измерений:
Поправки вычисляют в табл. 3, вначале piνi, как сумму произведений по строке коэффициентов условных уравнений на соответствующие коррелаты, затем νi:
После этого делают контроль поправок: [pν²]= -[кw] и по формуле (16) в схеме решения нормальных уравнений.
Вычислим уравненные значения измеренных величин:
Контроль уравнивания:
Вычислим отметку определяемого пункта:
Выполним оценку точности по материалам уравнивания.
- средняя квадратическая ошибка единицы веса (превышения по ходу в 1 км).
- средняя квадратическая ошибка функции.
2.9. Уравнивание геодезического четырехугольника коррелатным способом
Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
Рис. 2. Геодезический четырехугольник
Таблица 5
Результаты измерений
|
№ углов |
Измеренные углы βi |
№ углов |
Измеренные углы βi |
|
1 |
77°35′ 46,3″ |
5 |
36°00′ 05,7″ |
|
2 |
57° 00′ 57,0″ |
6 |
46° 29′ 49,3″ |
|
3 |
27° 22′ 57,6″ |
7 |
37° 54′ 10,8″ |
|
4 |
59° 35′ 57,7″ |
8 |
18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n - t = 8 - 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 - условных уравнения фигур и 1 - полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
1. 5 + ν5 + 2 + ν2 + 3 + ν3 + 4 + ν4 - 180° = 0;
2. 8 + ν8 + 1 + ν1 + 6 + ν6 + 7 + ν7 - 180° = 0;
3. 1 + ν1 + 2 + ν2 + 3 + ν3 + 8 + ν8 - 180° = 0.
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс - точка А, то
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
1) ν5 + ν2 + ν3 + ν4 + w1 = 0; w1 = 5 + 2 + 3 + 4 - 180°= -2,0″;
2) ν8 + ν1 + ν6 + ν7 + w2 = 0; w2 = 8 + 1 + 6 + 7 - 180°= +2,1″;
3) ν1 + ν2 + ν3 + ν8 + w3 = 0; w3 = 1 + 2 + 3 +8 - 180°= -3,4″.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
.
.
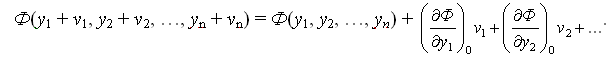Частная производная функции Ф4 по аргументу β5 (углу числителя):
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
Умножив на ρ″, получим
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
Таблица 6
Вычисление Δi и w″4
|
... |
Числитель |
... |
... |
Знаменатель |
... |
|
№ углов |
βi |
Δi |
№ углов |
βi |
Δi |
|
5 |
36°00′ 05,7″ |
1,38 |
3+4 |
86°58′ 55,3″ |
0,05 |
|
8+7 |
55° 54′ 26, 5″ |
0,68 |
6 |
46° 29′ 49,3″ |
0,95 |
|
3 |
27° 22′ 57,6″ |
1,93 |
8 |
18° 00′ 15,7″ |
3,08 |
w″4 = +2,67″.
Полюсное условное уравнение поправок принимает вид:
4) 1,38 ν5 + 0,68 ν7 + 1,88 ν3 - 0,05 ν4 - 0,95 ν6 - 2,40 ν8 + 2,67 = 0.
Составим весовую функцию.
Пусть
- дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
(24)
и весовая функция:
Коэффициенты условных уравнений и функции поместим в табл. 7.
Таблица 7
Коэффициенты условных уравнений и функции
|
№ измерения |
a |
b |
c |
d |
f |
ν |
|
1 |
0 |
1 |
1 |
0 |
0 |
... |
|
2 |
1 |
0 |
1 |
0 |
-1 |
... |
|
3 |
1 |
0 |
1 |
+1.88 |
0 |
... |
|
4 |
1 |
0 |
0 |
-0.05 |
0 |
... |
|
5 |
1 |
0 |
0 |
+1.38 |
0 |
... |
|
6 |
0 |
1 |
0 |
-0.95 |
0 |
... |
|
7 |
0 |
1 |
0 |
+0.68 |
0 |
... |
|
8 |
0 |
1 |
1 |
-2.40 |
0 |
... |
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения - m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции - mF.
Вычислите уравненные значения углов
и
сделайте контроль уравнивания.