3.5. Решение нормальных уравнений способом обращения

Умножив систему нормальных уравнений NttXt1 + Bt1 = 0 на обратную матрицу N-1

получают:

(34)

(35)

- решение нормальных уравнений способом обращения.

По определению обратной матрицы, N-1N = E. Это равенство используется для обоснования способа определения элементов обратной матрицы. Пусть t = 2.

Отсюда следует:

- 1-я система весовых нормальных уравнений.

- 2-я система весовых нормальных уравнений.

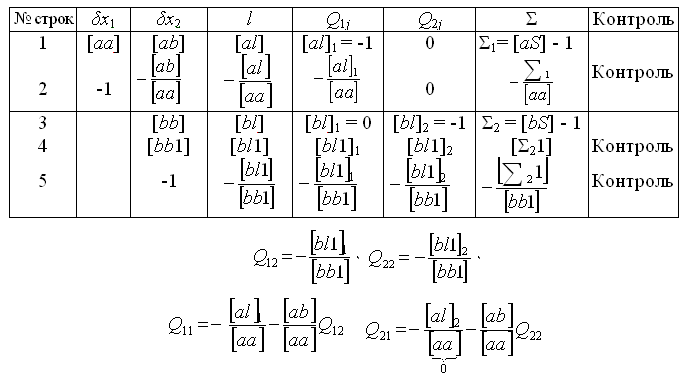
В общем случае в результате подобных действий получится t систем весовых нормальных уравнений по t уравнений в каждой системе. Эти системы имеют такую же матрицу коэффициентов, как и основная, с неизвестными δхj и отличаются от нее только столбцами свободных членов. В j-ом уравнении j-ой системы свободный член равен -1, остальные равны нулю. Системы весовых нормальных уравнений решают параллельно с основной системой, в общей схеме, с использованием дополнительных столбцов для свободных членов этих систем (табл. 9). Для контроля вычисленные значения элементов обратной матрицы Qij подставляют в суммарные уравнения, составленные для весовых систем. Например, для t = 2 эти уравнения будут иметь вид:

([paa] + [раb])Q11 + ([pab] + [pbb])Q12 - 1 = 0;

([paa] + [pab])Q21 + ([pаb] + [pbb]) Q22 - 1 = 0.

Для предварительного контроля служат равенства Qij = Qji (i ≠ j).

Элементы обратной матрицы Qij называют весовыми коэффициентами.

Таблица 9

Определение элементов обратной матрицы в схеме Гаусса

3.6. Оценка точности по материалам уравнивания

Среднюю квадратическую ошибку функции параметров определяют по формуле:

где

(36)

- средняя квадратическая ошибка единицы веса;

(37)

- обратный вес функции параметров или в матричном виде:

(38)

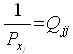(39)

- обратный вес параметра, равный диагональному элементу обратной матрицы.

3.7. Блок-схема параметрического способа уравнивания

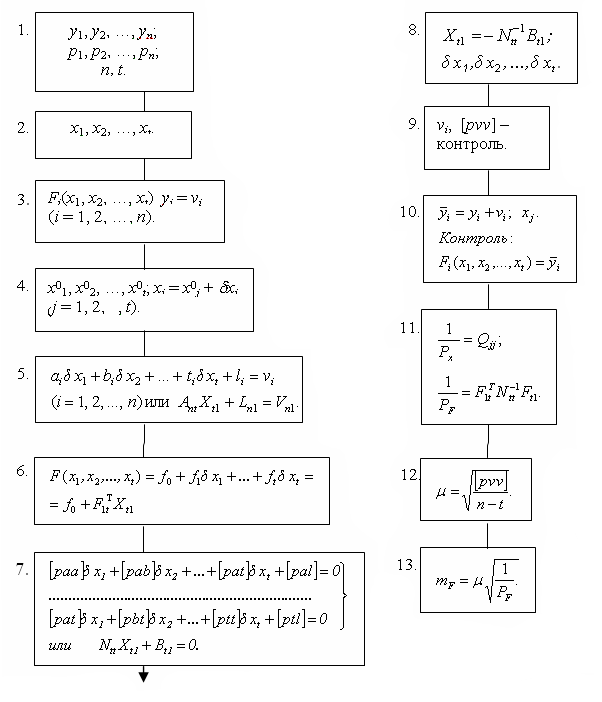
1. Анализируют совокупность измерений yi, определяют t - число необходимых измерений. Устанавливают систему весов измерений pi (i = 1, 2, ..., n).

2. Выбирают независимые параметры х1, х2, ..., хt, число которых равно t.

3. Составляют параметрические уравнения связи. Уравненные значения всех измеренных величин выражают в виде функций выбранных параметров.

4. Находят приближенные значения параметров х0j.

5. Параметрические уравнения связи приводят к линейному виду, вычисляют коэффициенты и свободные члены параметрических уравнений поправок.

6. Составляют функцию параметров для оценки ее точности. Весовую функцию линеаризуют.

7. Составляют нормальные уравнения, вычисляют коэффициенты и свободные члены нормальных уравнений.

8. Решают нормальные уравнения, вычисляют поправки к приближенным значениям параметров и контролируют их.

9. Вычисляют поправки vi к результатам измерений, [pν²] и выполняют контроль νi и [pν²].

10. Вычисляют параметры, уравненные результаты измерений и выполняют контроль уравнивания.

11. Вычисляют обратные веса параметров и функций параметров.

12. Выполняют оценку точности результатов измерений, вычисляют среднюю квадратическую ошибку единицы веса.

13. Вычисляют средние квадратические ошибки уравненных величин.