Теоретические основы электротехники-1

Глава 5. Расчет цепей при синусоидальном и постоянном токах

233

Чтобы избавиться от мнимости в знаменателе, необходимо умножить числитель и знаменатель на сопряженную знаменателю комплексную величину. Например,

Y2			r2	jx2						r2	j		x2	g		jb2 .
		(r	jx	2	)(r jx	2	)		r 2	x 2		r 2	x 2		2
	2				2			2		2	2		2

Здесь интересно отметить, что, пользуясь комплексным методом, автомати- чески получаем соотношения между эквивалентными проводимостями g è b и сопротивлениями r è x цепи или ее участка, выведенные в § 4.8.

Первый участок соединен последовательно со взятыми вместе вторым и третьим участками. Следовательно, комплексное сопротивление всей цепи

Z Z1 Z 23 ,

ãäå

Z1 r1 jx1;	Z 23		1					1			g23	j	b23		.
			Y	23		g	23	jb		g2	b2		g2	b2
								23	23		23		23	23

Комплексный ток в неразветвленной части цепи

I1 UZ ,

причемU можно принятü вещественным, т. е.U U. Это значит, что вектор приложенного напряжения U направляем по оси вещественных. Комплексное напряжение на втором и третьем участках находим из равенств

U 23 U I1Z1 èëè U 23 I1Z 23 ,

после чего легко определяются комплексные токи в этих участках:

I	U Y		;	I	U Y		.
2	23	2		3	23	3

Зная комплексное сопротивление Z r + jx всей цепи, определяем угол сдвига 2 между напряжением U и током I из соотношения

2 arctg xr .

Пользуясь выражениями для активной и реактивной мощностей при последовательном и параллельном соединениях, нетрудно усмотреть, что и в случае смешанного соединения активная мощность всей цепи равна сумме активных мощностей, расходуемых на отдельных ее участках, а реактивная мощность всей цепи равна алгебраической сумме соответствующих реактивных мощностей.

5.8. О расчете сложных электрических цепей

Электрические цепи, схема которых не является простым сочетанием последовательного и параллельного соединений участков цепи, будем называть с л о ж - н ы м и ц е п я м и. Как уже было указано, можно произвести расчет любой сложной цепи, составив на основе законов Кирхгофа систему уравнений и решив ее. В общем случае применение законов Кирхгофа в сочетании с заданными зависимостями между напряжениями на отдельных элементах и токами в них приводит к системе дифференциальных уравнений. Применение комплексного метода

234 Часть 2. Теория линейных электрических цепей

позволяет найти частное решение системы дифференциальных уравнений в установившемся режиме при протекании синусоидальных токов в линейной электрической цепи. При этом дифференциальные уравнения для мгновенных искомых токов заменяются алгебраическими уравнениями для комплексных токов, напряжений и ЭДС.

Число независимых уравнений должно быть равно числу неизвестных. Если отыскиваются токи во всех ветвях, то число уравнений должно быть равно числу ветвей в цепи. Такое равенство имеет место в цепи, в которой отсутствуют идеальные источники тока. При наличии идеальных источников тока в s ветвях число уравнений будет меньше общего числа ветвей на эту величину s, так как в таких ветвях токи заданы независимо от режима в остальной цепи.

Таким образом, в самом общем случае максимальное число уравнений определяется числом ветвей p, не содержащих только идеальные источники тока. Источники тока, содержащиеся в обобщенных ветвях, не входят в это число.

В § 3.17 была получена полная система уравнений электрической цепи, в которую входили q – 1 уравнений, составленных для токов (в узлах или в сечениях) согласно первому закону Кирхгофа, и n p – q + 1 уравнений, составленных для напряжений (в контурах) согласно второму закону Кирхгофа.

В матричной форме с учетом перехода от мгновенных токов и напряжений к комплексным токам и напряжениям можно записать q – 1 уравнений Кирхгофа

для узлов AI A=

или для сечений DI D=

è n p – q + 1 уравнений Кирхгофа для контуров

CU CE,

ãäå

I1

=1

U1

E1

I

;

=

; U

;

E

I p

= p

U p

E p

— матрицы-векторы (матрицы-столбцы) порядка p ? 1; A — матрица узловых соединений порядка (q – 1) ? p; D — матрица сечений порядка (q – 1) ? p; C — матрица контуров порядка n ? p. Напомним, что первое число определяет число строк матрицы, а второе — число столбцов. Все матрицы упорядочены, т. е. сна- чала пронумерованы ветви дерева (от 1 до q – 1), а затем уже связи (от q äî p).

Применение комплексного метода требует записи в комплексной форме всех заданных ЭДС, токов источников и зависимостей между токами и напряжениями. Учитывая особенности линейных цепей и перехода от дифференциальных уравнений к их алгебраическим изображениям, для пассивных элементов обобщенной ветви можем записать

1

U

k

r I

k

j0L

I

k

I

k

Z

k

I

k

èëè I

k

Y

U

k

.

k

k

j0Ck

k

Такие уравнения могут быть записаны для p ветвей электрической цепи. Введем в рассмотрение м а т р и ц у с о п р о т и в л е н и й и м а т р и ц у п р о в о д и -

Глава 5. Расчет цепей при синусоидальном и постоянном токах

235

м о с т е й, представляющие собой квадратные матрицы порядка p ? p, состоящие из диагональных ненулевых элементов Zk è Yk соответственно:

1 . . .			.	p		1 . . .				.	p
1		0 . .	.	.		1		Y1	0 . . .		.
	Z1
.	0	Z 2 . .	.	.		.		0	Y2 . . .		.
Z .	.	. . .	.	.	;	Y .		.	. . . .		.	.
.	.	. . .	.	.		.		.	. . . .		.
.	.	. . .	Z p 1	0		.		.	. . .	Yp 1	0
p	.	. . .	0	Z p		p		.	. . .	0	Yp

Имеют место очевидные равенства

Z Y–1 è Y Z–1.

Уравнения, связывающие токи и напряжения пассивных частей ветвей, представляют собой законы Ома в комплексной форме. В матричной форме закон Ома будет иметь вид

U ZI èëè I Z–1U YU.

С учетом последних равенств можем составить систему из p уравнений для искомых p напряжений

AI AYU A= (èëè DYU D=) è CU CE, или составить систему из p уравнений для искомых p токов

CU CZI CE è AI A= (èëè DU D=).

Ðèñ. 5.5

В качестве примера рассмотрим цепь, изображенную на рис. 5.5, à. Íà ðèñ. 5.5, á эта цепь представлена в виде двухполюсников с комплексными параметрами. Граф схемы (рис. 5.5, á), изображенный на рис. 5.5, â, совпадает с гра-

236 Часть 2. Теория линейных электрических цепей

фом схемы (рис. 5.5, à), для которой в § 3.17 мы записали систему дифференциальных уравнений. Пусть заданы ЭДС и ток источника тока:

e1 E1m (sin0t Α 1); e3 E 3m (sin0t Α 3 ); e5 E 5m (sin0t Α 5 );

=6 = 6m (sin0t Α 6 ),

àтакже параметры r, L, C в ветвях цепи.

Для расчета с помощью комплексного метода мы должны записать исходные данные цепи (рис. 5.5, á) â âèäå

			E1m				jΑ			E					jΑ										E		3m jΑ				3		E 3 e								jΑ	3										E 5m							jΑ	5	E 5 e	jΑ	5
								1								1
E1						e							1e				;				E 3								e															; E 5													e							;
		2																									2																									2
							= 6m					jΑ6										jΑ6					1 r1 j0L1																									1
		= 6									e				= 6 e									; Z														; Z 2																		;
																																																		j0C2
									2
						Z			(r				r ) j0 (L														L )								1						; Z								r							j0L					;
							3																																							4														4
											3					3								3				3						j0C3																4
																Z					j0L						; Z					r										1					.
																			5							5				6
																																6							j0 C6
Для графа схемы (рис. 5.5, â) согласно § 3.13 и 3.14 имеем:
																					1				2			3				4									5					6
																	1				1							1																		–1
													A 2
																				–1					1									–1																	;
																	3												–1				1						–1
														1							2			3				4				5						6
											4		–1											1				1
							C 5
													1								1		–1									1																F					1					.
											6			1							1																	1

Запишем в матричной форме все исходные данные:

										0
	I1			U	1		E1
	I 2			U	2		0			0
I			U			; E				0
	I 3	;		U 3			E 3	;	=		;
	I 4			U	4		0			0
										0
	I 5			U 5			E 5
	I 6			U			0
					6					= 6
6?1			6?1				6?1			6?1

Глава 5.				Расчет цепей при синусоидальном и постоянном токах 237
	Z1
		Z2
Z			Z3				diag (Z1Z2Z3Z4Z5Z6).
				Z4
					Z5
						Z6

6?6

Символ diag означает, что матрица Z — квадратная, диагональная и ее диагональными элементами являются записанные в скобках величины.

Тогда система узловых уравнений Кирхгофа для токов может быть представлена в матричной форме:

	1
		I1	I 3	I 6		=6
AI	2	I1 I 2 I 4				0	;
[(q 1)?p]?( p?1)
	3	I 3 I 4 I 5				0

(q–1)?1

Падения напряжений в ветвях можно представить в виде вектора U ZI, êî-

Z1I1

торый ввиду диагональности матрицы Z будет иметь вид Z 2 I 2 .

Падение напряжений и ЭДС в контурах можно представить в виде CU è CE. Тогда система контурных уравнений согласно второму закону Кирхгофа будет иметь вид

4

Z

Z

Z

1I1

3 I 3

4 I 4

E1

E 3

CU

CZI

5

Z

Z

Z

Z

CE .

1I1

2 I 2

3 I 3

5 I 5

E

1 E

3 E 5

(n?p)?( p?1)

(n?p)?( p?p)?( p?1)

6

Z

Z

Z

1I1

2 I 2

6 I 6

E1

(n?1)

Итак, произведение диагональной матрицы Z на столбцовую матрицу I определяет также столбцовую матрицу, строками которой являются произведения диагональных элементов (в данном случае комплексные сопротивления ветвей)

238 Часть 2. Теория линейных электрических цепей

на токи соответствующих ветвей. Это обстоятельство облегчает выполнение такого матричного перемножения. Перемножение прямоугольных матриц A è C на столбцовые матрицы сводится к суммированию тех элементов строк столбцовой матрицы, номера которых соответствуют номерам ненулевых элементов столбцов прямоугольных матриц. По этой причине можно, рассматривая только матрицу A, èëè C, èëè D, записать соответствующее уравнение для данного контура, или узла, или сечения. Например, в контурное уравнение, записанное для контура 5, образованного связью 5 (см. строку 5 матрицы C), должны входить напряжения (а следовательно, и ZI) ветвей 1, 2, 5 со знаком «плюс» (в строке 5 эти столбцы имеют положительные ненулевые элементы) и ветви 3 со знаком «минус (в строке 5 столбец 3 имеет отрицательный ненулевой элемент). Соответственно, для этого контура имеем

U1 U 2 U 3 U 5 Z1I1 Z 2 I 2 Z 3 I 3 Z 5 I 5 .
							0, òî
В контур 5 входят ЭДС именно этих же ветвей. Поскольку E 2
Z1I1	Z 2 I 2	Z 3 I 3	Z 5 I 5	E1	E 3	E 5 .

Если расписать всю систему уравнений, получим для узлов 1, 2, 3, соответственно,

;

0

I1

I 3

I

6 = 6

I

1

I 2

I

4 0; I

3

I

4 I 5

и для контуров 4, 5 è 6, соответственно,

Z

Z

;

Z

Z

Z

1I1

3 I 3

Z 4 I 4

E1

E 3

Z1I1

2 I 2

3 I 3

5 I

5

;

Z

E1

E 3 E 5

1I1 Z 2 I 2 Z 6 I

6

E1.

Для расчета данной цепи, следовательно, необходимо решить систему из шести уравнений.

Трудность расчета сложных линейных цепей заключается в необходимости решать совместно p линейных алгебраических уравнений. В связи с этим представляют ценность методы, позволяющие тем или иным путем упростить задачу. Эти методы дают возможность или преобразовать цепь так, что расчет упрощается, или уменьшить число уравнений, или, наконец, расчленить сложную зада- чу на ряд более простых. В следующих параграфах будет рассмотрен ряд основных таких методов.

5.9. Расчет цепи, основанный на преобразовании соединения треугольником в эквивалентное соединение звездой

Для упрощения расчета сложной цепи в ряде случаев целесообразно осуществить преобразование некоторой части цепи. Эта часть цепи до ее преобразования должна быть эквивалентна этой же части цепи после ее преобразования при условии, что режим в остальной, не преобразованной части остается неизменным.

К числу таких преобразований относится, например, преобразование соединения треугольником в эквивалентное соединение звездой, которое рассмотрим в настоящем параграфе, а также преобразование нескольких параллельно соеди-

Глава 5. Расчет цепей при синусоидальном и постоянном токах 239

ненных ветвей с источниками ЭДС в одну эквивалентную им ветвь с одним источником ЭДС, что будет рассмотрено в следующем параграфе.

Íà ðèñ. 5.6, à между точками 1, 2 è 3 некоторой сложной цепи включены три участка с сопротивлениями Z1, Z2 è Z3, соединенные звездой. На рис. 5.6, á между

этими же точками включены три участка
Z12, Z23 è Z31, соединенные треугольником.
Остальная, не подвергающаяся преобра-
зованию, часть сложной цепи на рисунке
не показана.
Соединения звездой и треугольником
эквивалентны друг другу при условии,
что при одинаковых в обоих случаях на-
пряженияхU12 ,U	23 èU 31 между точками 1,	Ðèñ. 5.6
2 è 3 è òîêè I1, I 2	è I 3 , подходящие к этим

точкам от остальной части цепи, одинаковы в обоих случаях. Составим уравнения для соединения з в е з д о й:

I1 I 2 I 3 0;

U12 I1Z1 I 2 Z 2 I1Z1 (I1 I 3 )Z 2 I1(Z1 Z 2 ) I 3 Z 2 ;

U 23 I 2 Z 2 I 3 Z 3 (I1 I 3 )Z 2 I 3 Z 3 I1Z 2 I 3 (Z 2 Z 3 ).

Решая эти уравнения относительно токов I1 è I 3 , получим

	I1 U12	Z 2 Z 3	U 23	Z 2	;	I 3	U12	Z 2	U 23	Z1 Z 2	,
		D		D				D		D

ãäå

D Z1Z 2 Z 2 Z 3 Z 3 Z1.

Для соединения т р е у г о л ь н и к о м имеем уравнения

U12 U 23 U 31 0;

I

I

I

U

1

U

1

U

1

1

U

1

;

1

12

31

12

31

Z 31

12

Z12

Z 31

23

Z 31

Z12

I

I

I

U

1

U

1

U

1

U

1

1

.

23

3

31

23

31

Z 31

Z 23

12

Z 31

23

Z 31

Z 23

Òîêè I1 è I 3 , а следовательно, и ток I 2 I1 I 3

должны быть одинаковыми

в обеих схемах при одинаковых в обоих случаях напряжениях U12

è U 23 , причем

это должно быть справедливо при любых соотношениях междуU12

èU

23 . Следо-

вательно, коэффициенты в выражениях для токов I1 è I 3

должны быть одинако-

выми в случаях соединения звездой и треугольником. Получаем

Z 2 Z 3

1

1

;

Z 2

1

;

Z1 Z 2

1

1

.

D

Z12

Z 31

D

Z 31

D

Z 31

Z 23

Из этих уравнений определяются сопротивления искомого эквивалентного треугольника через заданные сопротивления звезды:

Z12 DZ 3 ; Z 23 DZ1 ; Z 31 DZ 2 ,

240 Часть 2. Теория линейных электрических цепей

ãäå

D Z1Z 2 Z 2 Z 3 Z 3 Z1.

Если заданы сопротивления треугольника и отыскиваются сопротивления эквивалентной ему звезды, то следует пользоваться формулами

Z1

Z12 Z 31

; Z

Z 23 Z

12

; Z 3

Z 31Z

23

.

Z12

Z 23

Z

31

2

Z12

Z 23

Z 31

Z12

Z 23

Z

31

Например, формула для Z1 легко получается, если заметить, что

Z

Z

D 2

è Z

Z

Z

D 2

.

12

31

Z 2 Z

12

23

31

Z1Z 2 Z 3

3

При эквивалентном преобразовании треугольника в звезду и наоборот возможны случаи, когда это преобразование теряет смысл, что имеет место при равенстве нулю сумм сопротивлений или проводимостей. Возможны и случаи, когда эквивалентное преобразование приводит к появлению отрицательных активных сопротивлений в отдельных лучах звезды или сторонах треугольника, означающему невозможность реали-

Ðèñ. 5.7 зации таких схем при помощи одних элементов r, L, C. На ход расчета последнее

обстоятельство не влияет. В окончательном выражении комплексное сопротивление всей пассивной цепи содержит положительную вещественную часть.

Упрощение расчета сложной цепи при помощи эквивалентного преобразования конфигурации цепи можно проследить на примере расчета цепи, изображенной на рис. 5.7, à. В этой цепи упрощение достигается преобразованием треугольника Z12, Z23, Z31 (ðèñ. 5.7, à) в эквивалентную звезду Z1, Z2, Z3 (ðèñ. 5.7, á). После такого преобразования получаем простую цепь с последовательно-параллельным соединением участков.

5.10. Преобразование источников ЭДС и тока

Для удобства расчета электрических цепей иногда полезно производить замену источника ЭДС эквивалентным источником тока или выполнять обратную замену источника тока эквивалентным источником ЭДС.

Источники ЭДС и тока являются эквивалентными, если они обладают одной и той же внешней характеристикой u f (i) (èëè i 2 (u)). При присоединении к ним приемника с некоторым сопротивлением rïð 1/gïð (èëè Zïð 1/Yïð) напряжение u (èëè U) è òîê i (èëè I) в приемнике будут в обоих случаях одинаковы.

	Уравнение внешней характеристики источника ЭДС имеет вид u e – râíi
(èëèU		E	Z âí I). Запишем это уравнение иначе, а именно: i e/râí – u/râí (èëè
I	E Z âí	U Z âí ). Уравнение внешней характеристики источника тока имеет
âèä i = – ugâí (èëè I				= YâíU). Эти внешние характеристики совпадут, если

соблюдать условия

Глава 5. Расчет цепей при синусоидальном и постоянном токах

241

e

1

1

E

=

è gâí

èëè

=

è

Yâí

.

râí

râí

Z âí

Z âí

По этим равенствам можно вычислить параметры = è gâí (= è Yâí) источника -

тока, эквивалентного заданному источнику ЭДС, имеющему параметры e è râí (E

è Zâí). Соответственно, из соотношений

e = gâí

è râí 1 gâí

èëè

è

Z âí

1 Yâí

E = Yâí

можно получить параметры источника ЭДС, эквивалентного источнику тока. Эквивалентные замены могут бытъ произведены и для зависимых источников. Пусть в некоторой ветви p с проводимостью Yp имеется зависимый, управляемый током I q ветви q источник тока = p I q . Согласно вышеприведенным фор-

мулам, можно преобразовать управляемый током источник тока в управляемый

током источник ЭДС. Значение ЭДС будет равно E p

I q /Yp, и внутреннее со-

противление Zâí Zp 1/ Yp.

Преобразуем две параллельно соединенные ветви, содержащие источники

1/ Y1 è Z2 1/ Y2 (рис. 5.8), в одну эквивалент-

ÝÄÑ E1

è E 2 и сопротивления Z1

ную ветвь.

Рассматривая параллельно соединенные на рис. 5.8 ветви как источники ЭДС

с внутренними сопротивлениями Z1 è Z2, заменим их эквивалентными ис-

E1

è E 2

с внутренними проводимостями Y1 1/ Z1 è

точниками тока =1

E1Y1

è =2

E 2 Y2

Y2 1/ Z2 (рис. 5.8). Объединив эти два источника тока в один = =1

=2 ñ âíóò-

ренней проводимостью Y Y1 + Y2, перейдем от него к источнику ЭДС

=

E1Y1

E1Y2

E1

Y

Y1

Y2

с внутренним сопротивлением Z

1

.

Y Y

2

1

Ðèñ. 5.8

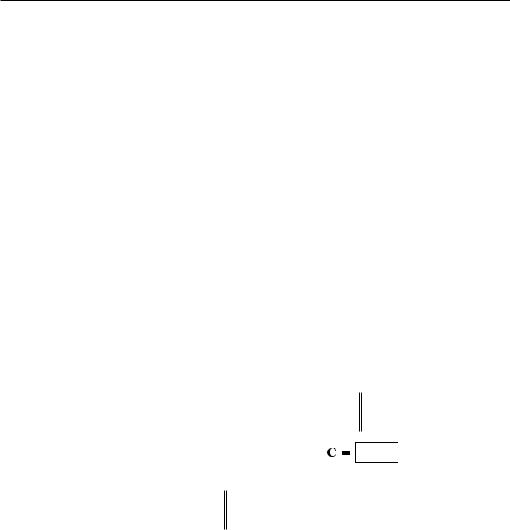
Распространяя полученный результат на n параллельно соединенных ветвей, найдем, что заменяющая их эквивалентная ветвь содержит источник ЭДС.

						n
						E kYk
		E1Y1	E1Y2	E nYn		k 1
E
						n

Y1 Y2	Yn	Yk
		k 1

242 Часть 2. Теория линейных электрических цепей

и сопротивление

Z			1		.
	Y Y	2	Y
1				n

5.11. Метод контурных токов

То обстоятельство, что контур, образованный данной связью графа схемы, проходит только по ветвям дерева, дает возможность выразить токи в ветвях дерева через токи в связях. Такая связь в матричном виде записывается следующим образом (см. § 3.16):

			~	~
	~		I1	D2I2 .
		— матрица-столбец порядка (q – 1)				? 1, элементами которой являются
	Здесь I1
	~	~		~			— матрица-столбец порядка n ? 1,
	òîêè I I		в обобщенных ветвях дерева; I		2
	1	q 1						~	~
	элементами которой являются токи обобщенных ветвей-связей графа							I q	I p .

Напомним, что в обобщенных ветвях наряду с пассивными элементами Z è Y содержатся также источники ЭДС и тока (см. § 3.10). Подматрица D2 – Ft является прямоугольной матрицей порядка (q – 1) ? n, состоящей из элементов ±1 и 0. Строки этой матрицы нумеруются согласно номерам ветвей дерева, а столбцы — согласно номерам связей графа схемы (см. § 3.15). Матрицу-столбец токов во всех ветвях графа схемы можно определить через матрицу токов в связях, имея в виду, что

~

~

D

~

D2

~

F

t

I1

2I

2

I

~

~

1

I2

I2

I

2

1

~

Сравнивая множитель-матрицу у I2 с матрицей что имеет место равенство

F t C t .

1

~

I2 .

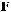
, можно заметить,

Таким образом, токи во всех обобщенных ветвях графа схемы выражаются
~
через матрицу токов в связях (I2 ) равенством
~	t~
I	C I2 .
	~		, называют контур-
Токи в связях, записанные в матричной форме буквой I		2

ными токами, так как связи и определяют контуры. Контурные токи, число которых равно n, можно принять за искомые неизвестные и составить уравнения именно для них. Напомним, что матричная связь между токами ветвей дере-

ва и токами связей графа схемы получена из матричного равенства ~ 0

DI

(см. § 3.15), записанного на основе первого закона Кирхгофа применительно к сечениям графа схемы.

Уравнения на основе второго закона Кирхгофа записываются в виде

~	èëè CU CE,
CU 0